leetcode 982 668

题意：寻找一个整数数组A中的三个数，使得它们与为0

思路：使用 unordered_map , key键存储两层for循环后得到的与值，再将unordered_map的所有key值与A里的所有值相与，若为0则将 A.second 加到cnt中。

class Solution {
public:
    int countTriplets(vector<int>& A) {
        int cnt = 0;
        unordered_map<int , int> tri;
        for(auto i:A)
            for(auto j : A)
                ++tri[i&j];
        for(auto k:A)
            for(auto t:tri)
                if((k & t.first) == 0)
                    cnt += t.second;
        return cnt;
    }
};

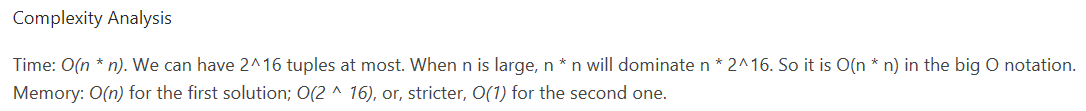
时间复杂度分析：因为A[i]的最大值为2^16，所以map的最多存储2^16个数，时间复杂度为  O(n*n).

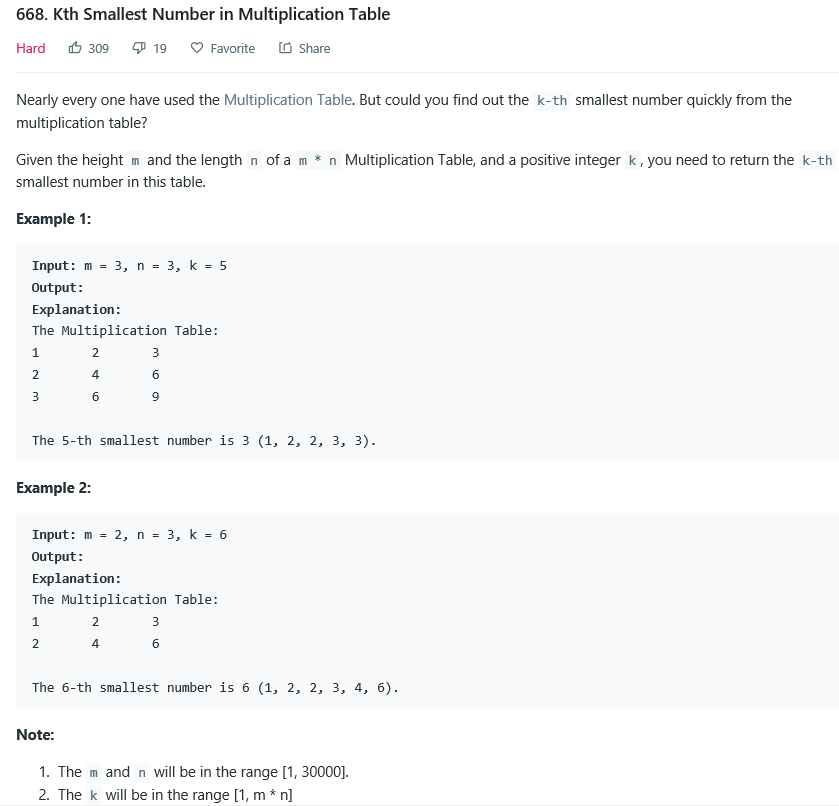
题意：已知一个m*n的乘法表，如第m行n列的元素为m*n，寻找第k大的数字。

思路：二分搜索。

1）已知乘法表中最小的数为1，最大的数为m*n，可以得到mid = (1+m*n)/2；

2）设 cnt = 比mid小的数字的个数。循环让mid 整除 从 1 到 m， 若得到的数 > n, 则将cnt+=n; 否则 cnt+=mid/2。

3）二分搜索查找时，当cnt==k，不能直接返回mid，因为mid可能不在乘法表里；当退出while循环，即 left==right 时，返回right或者left 为找到的第k大的数字。

class Solution {
 public:
     int findKthNumber(int m, int n, int k) {
         int left = 1;
         int right = m*n;
         
         while(left < right){
             int cnt = 0;
             int mid = (left+right)/2;
             for(int i=1; i<=m; i++){
                 cnt += (mid > i*n)? n : (mid/i);
             }
             if(cnt<k)
             {
                 //在mid右边找
                 left = mid+1;
             }
             else
                 //cnt>=k 在左边找
                 right = mid;
         }
         return right;
     }
 };