注:其实从中学就开始学习统计学了,最早的写"正"字唱票(相当于寻找众数),就是一种统计分析的过程。还有画直方图,求平均值,找中位数等。自己在学校里并没有完整系统的学习过概率论和数理统计,直到在工作中用到,才从最初的印象中,逐渐把这门学科与整个数学区分开来。自从认识到这门学科在自己从事的工作(数据分析)中所处的重要地位,真没少花时间在这方面的学习上。从最初的p值的含义,到各种分布,假设检验,方差分析。。。有的概念看过很多遍,但还是没有理解透彻;有的看过,长时间不用,又忘记了。总之,这一路走来,实在是崎岖坎坷。因此,打算在最近专门抽出一段时间对自己学习过的《概率论与数理统计》做一个小结,也算是对自己的一个交代。主要包括以下几个方面:
- 基本概念;
- Python的实现;
- 一些比较经典的例子。
以下主要根据浙江大学在中国大学MOOC上的公开课笔记,整理而来:
基础中的基础
统计规律性:
在所有可观察的现象中,可以从大的方面分为两类——必然现象和随机现象。
物理学中各种定律描述的基本上都是必然现象,比如物体会因为重力而从高处下落,某一时刻地球位于太阳系中的位置。这些现象的发生都是确定无疑的,如果我们完全认识了它们的内在规律,那么在发生之前就是可以完全准确的预测出结果。但是还有一类现象是不确定的。它的不确定性表现在,事先无法准确的预测其结果。唯一可以获得这类现象的结果的办法是等到它们发生之后。最典型的例子就是抛硬币。抛一枚均匀的硬币之前,已知结果只有正面和反面两种,但是无法知道到底会是哪一面。生活中还有很多这样的事情,比如说,跟喜欢的人表白;明天是否会下雨等。可以看到,这些现象单次发生的时候,是毫无规律可循的。也正是有了这两种现象,才让这个世界既可以被认识,又不至于完全可以被预测(那不知道会多无聊)。
但当我们在相同的条件下,大量重复(如果可以的话)做某件不确定的事,然后统计实验结果,就有可能发现某种规律。还是拿抛硬币来举例,每次抛硬币都不知道会得到正面还是反面,但如果有耐心将一枚均匀的硬币抛20,000次(已经有多位著名的统计学家这么做过了),然后统计一下正反面分别出现了多少次,就可以发现它们差不多都是10,000次,也就是差不多各占50%。上面的抛硬币的例子中,随机现象(抛硬币)在相同的条件下,大量重复试验中呈现的规律性就叫做统计规律性。《概率论与数量统计》就是研究随机现象的统计规律的一门学科。从这里也可以看到样本量的多少对研究随机变量的规律的影响是巨大的。
概率论与数理统计:
实际上,一般概率论与数理统计被认为是两个学科。
概率论是数学的一个分支,研究如何定量描述随机变量及其规律;
数理统计则是以数据为唯一研究对象,包括数据的收集、整理、分析和建模,从而对随机现象的某些规律进行预测或决策。
怎么学习概率论与数量统计:
- 学思想:如何看待和处理随机规律性;
- 学方法:建立统计模型;
- 学应用:模型的实际应用,也可以自己收集、寻找各种实例;
- 学软件:掌握统计软件的使用和结果分析。
检验标准:对"随机"有足够的认识;对"数据"有兴趣、有感觉。
随机试验与样本空间
随机试验:
对随机现象的观察、记录、实验统称为随机试验。它具有以下特性:
- 可以在相同条件下重复进行;
- 事先知道所有可能出现的结果;
- 进行试验前不知道哪个试验结果会发生。
随机试验有很多种,例如常出现的掷骰子,摸球,射击,抛硬币等。所有的随机试验的结果可以分为两类来表示:
- 数量化表示:射击命中的次数,商场每个小时的客流量,每天经过某个收费站的车辆等,这些结果本身就是数字;
- 非数量化表示:抛硬币的结果(正面/反面),化验的结果(阳性/阴性)等,这些结果是定性的,非数量化的。但是可以用示性函数来表示,例如可以规定正面(阳性)为1,反面(阴性)为0,这样就实现了非数量化结果的数量化表示。
样本空间:
随机试验的所有可能结果构成的集合。一般即为S(大写的S)。
S中的元素e称为样本点(也可以叫做基本事件);
事件是样本空间的子集,同样是一个集合;
事件的相互关系:
- 事件的包含:A⊆B
- 事件的相等:A=B
- 事件的积(交):A∩B,AB
- 互斥事件(互不相容事件):不能同时出现
- 事件的和(并):A∪B
- 事件的差:A-B,A发生,B不发生
- 对立事件(逆事件):互斥,必需出现其中一个
频率与概率
频率:
频率是0~1之间的一个实数,在大量重复试验的基础上给出了随机事件发生可能性的估计。
频率的稳定性:在充分多次试验中,事件的频率总在一个定值附近摆动,而且,试验次数越多摆动越小。这个性质叫做频率的稳定性。
概率:
概率的统计性定义:当试验次数增加时,随机事件A发生的频率的稳定值p就称为概率。记为P(A)=p
概率的公理化定义:设随机试验对于的样本空间为S。对每一个事件A,定义P(A),满足:
- 非负性:P(A) ≥ 0;
- 规范性:P(S) = 1;
- 可列可加性:A1, A2, ...两两互斥,及AiAj = ∅, i≠j, 则P(∪Ai) = ∑P(Ai)
条件概率:
P(A|B)表示在事件B发生的条件下,事件A发生的概率,相当于A在B中所占的比例。此时,样本空间从原来的完整样本空间S缩小到了B
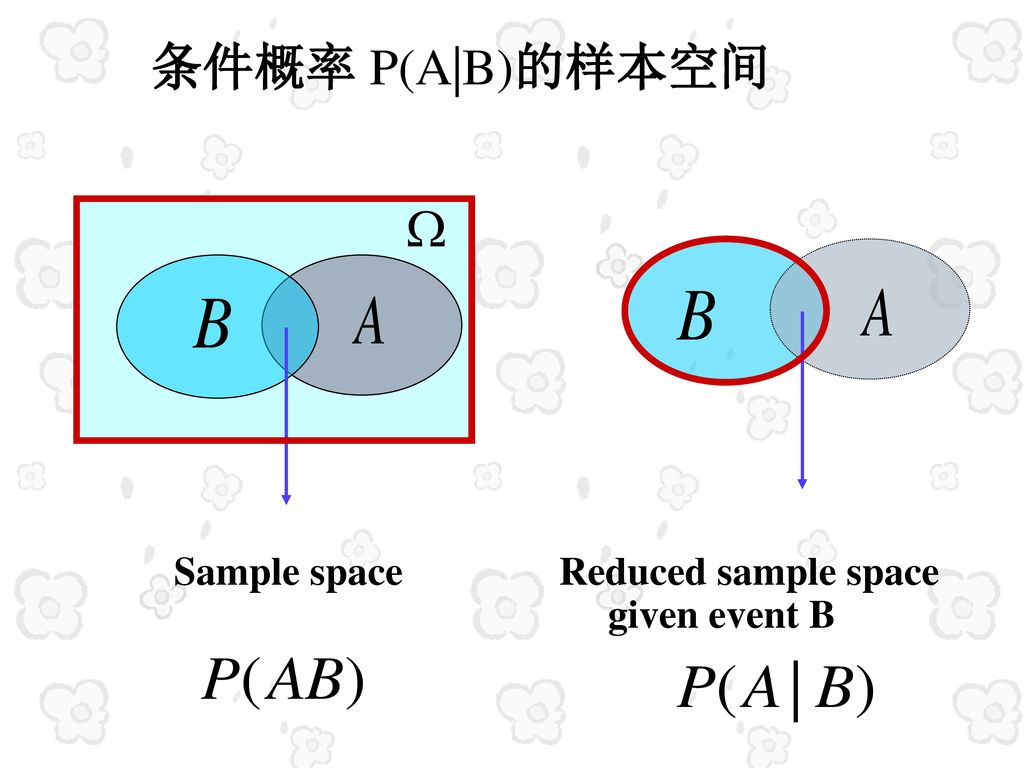
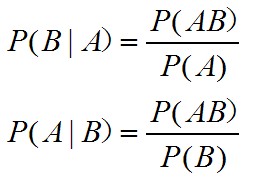
图1:a.条件概率的样本空间;b.条件概率的计算公式
例:一个家庭中有两个小孩,已知至少一个是女孩,问两个都是女孩的概率是多少?
(假定生男生女是等可能的)
解:由题意,样本空间为
S = {(兄, 弟), (兄, 妹), (姐, 弟), (姐, 妹)}
B = {(兄, 妹), (姐, 弟), (姐, 妹)}
A = {(姐, 妹)}
由于事件B已经发生,所以这时试验的所有可能只有三种,而事件A包含的基本事件只占其中的一种,所以有:
P(A|B) = 1/3,
即在已知至少一个是女孩的情况下,两个都是女孩的概率为1/3。
在这个例子中,如果不知道事件B发生,则事件A发生的概率为P(A) = 1/4
这里P(A) ≠ P(A|B),其原因在于事件B的发生改变了样本空间,使它由原来的S缩减为新的样本空间SB = B。
随机变量
在几乎所有的教材中,介绍概率论时都是从事件和样本空间说起的,但是后面的概率论都是围绕着随机变量展开的。可以说前面的事件和样本空间都是引子,引出了随机变量这个概率论中的核心概念。后面的统计学是建立在概率论的理论基础之上的,因此可以说理解随机变量这个概念是学习和运用概率论与数理统计的关键。
名词解释:
- 首先这是一个变量,变量与常数相对,也就是说其取值是不明确的,其实随机变量的整个取值范围就是前面说的样本空间;
- 其次这个量是随机的,也就是说它的取值带有不确定性,当然是在样本空间这个范围内。
定义:
设随机试验的样本空间是S。若对S中的每个样本点e,都有唯一的实数值X(e)与之对应,则称X(e)为随机变量,简记为X。
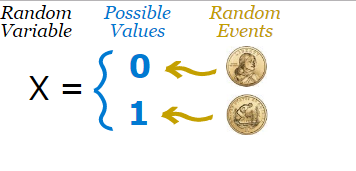
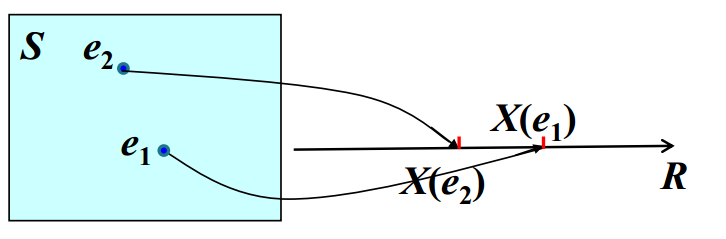
图2:a.随机变量与事件的关系;b.随机变量的本质是函数(一种映射关系)
随机变量的定义并不复杂,但是理解起来却并不是那么直观。参考图2的两个示意图,可以帮助理解。
- 首先,随机变量与之前定义的事件是有关系的,因为每个样本点本身就是一个基本事件;
- 在前面随机试验结果的表示中提到,无论是数量化的结果还是非数量化的结果,即不管试验结果是否与数值有关, 都可以引入变量, 使试验结果与数建立对应关系;
- 随机变量本质上是一种函数,其目的就是建立试验结果(样本空间中的点,同基本事件e)与实数之间的对应关系(例如将"正面"映射为1,"反面"映射为0);
- 自变量为基本事件e,定义域为样本空间S,值域为某个实数集合,多个自变量可以对应同一个函数值,但不允许一个自变量对应多个函数值;
- 随机变量X取某个值或某些值就表示某种事件,且具有一定的概率;
- 随机变量中的随机来源于随机试验结果的不确定性;
随机变量的表示:
- 随机变量通常用大写字母X, Y, Z或希腊字母ξ, η等表示;
- 随机变量的取值一般用小写字母x, y, z等表示。
通过引入随机变量,我们简化了随机试验结果(事件)的表示,从而可以更加方便的对随机试验进行研究。
图3:从事件到随机变量
- 事件A=“收到不少于1次呼叫” <=> ( X >= 1 );
- 事件B=“没有收到呼叫” <=> ( X = 0 ) ;
- 而P(A) = P(X >= 1), P(B) = P(X = 0)。
随机变量的分类:
- 离散型随机变量;
- 连续型随机变量;
- 每类随机变量都有其独特的概率密度函数和概率分布函数。
随机变量的数字特征:
- 期望(均值),众数,分位数,中位数;
- 方差;
- 协方差;
- 相关系数。
欢迎阅读“概率论与数理统计及Python实现”系列文章
Reference
中国大学MOOC:浙江大学,概率论与数理统计
中国大学MOOC:哈尔滨工业大学,概率论与数理统计
https://www.mathsisfun.com/data/random-variables.html
重大修订版:
2017-7-23,添加随机变量相关内容;