基于神经网络方法求解RL
项目地址:https://gitee.com/paddlepaddle/PARL/tree/develop/examples/tutorials/lesson3/dqn
1.函数逼近与神经网络
Lesson2中所述Sarsa、Q-learning均建立在Q表格的基础上,实际问题中状态数目往往不可数,因此需要值函数的近似。
值函数具有以下优点:
- 需要存储空间小
- 泛化性能强,相似状态输出相同
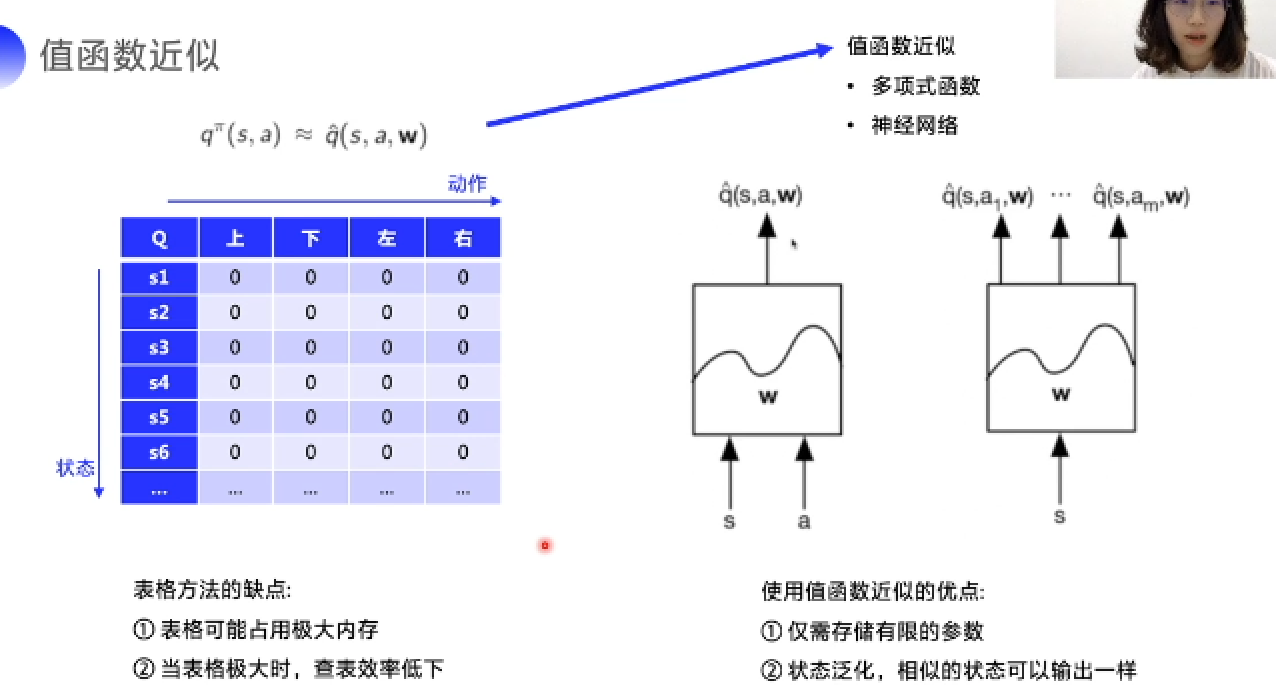
神经网络 & Paddle
下图为拟合一个四元一次方程的,基于paddle的神经网络代码
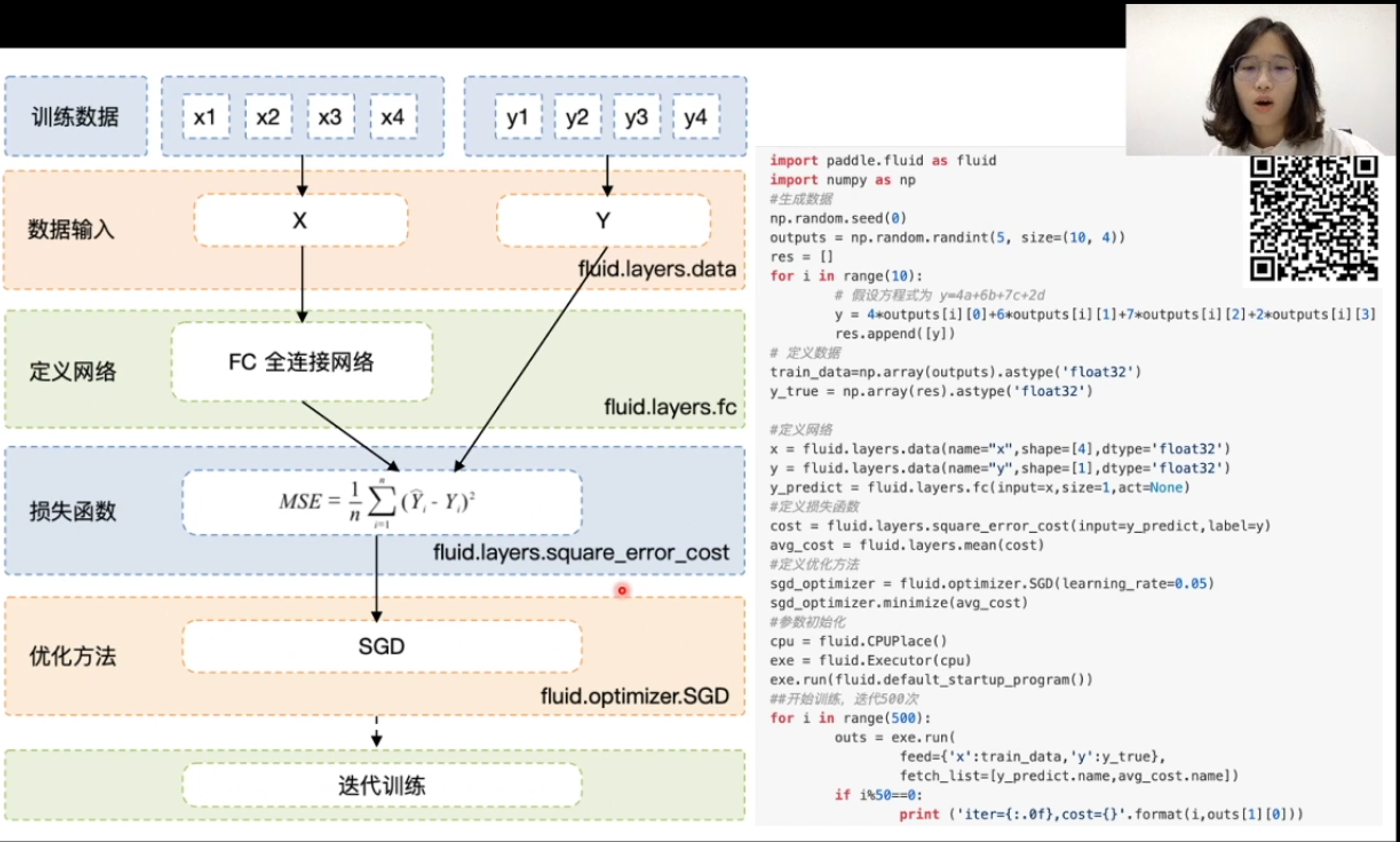
#加载库
import paddle.fluid as fluid
import numpy as np
#生成数据
np.random.seed(0)
outputs = np.random.randint(5, size=(10, 4))
res = []
for i in range(10):
# 假设方程式为 y=4a+6b+7c+2d
y = 4*outputs[i][0]+6*outputs[i][1]+7*outputs[i][2]+2*outputs[i][3]
res.append([y])
# 定义数据
train_data=np.array(outputs).astype('float32')
y_true = np.array(res).astype('float32')
#定义网络
x = fluid.layers.data(name="x",shape=[4],dtype='float32')
y = fluid.layers.data(name="y",shape=[1],dtype='float32')
y_predict = fluid.layers.fc(input=x,size=1,act=None)
#定义损失函数
cost = fluid.layers.square_error_cost(input=y_predict,label=y)
avg_cost = fluid.layers.mean(cost)
#定义优化方法
sgd_optimizer = fluid.optimizer.SGD(learning_rate=0.05)
sgd_optimizer.minimize(avg_cost)
#参数初始化
cpu = fluid.CPUPlace()
exe = fluid.Executor(cpu)
exe.run(fluid.default_startup_program())
##开始训练,迭代500次
for i in range(500):
outs = exe.run(
feed={'x':train_data,'y':y_true},
fetch_list=[y_predict.name,avg_cost.name])
if i%50==0:
print ('iter={:.0f},cost={}'.format(i,outs[1][0]))
#存储训练结果
params_dirname = "result"
fluid.io.save_inference_model(params_dirname, ['x'], [y_predict], exe)
# 开始预测
infer_exe = fluid.Executor(cpu)
inference_scope = fluid.Scope()
# 加载训练好的模型
with fluid.scope_guard(inference_scope):
[inference_program, feed_target_names,
fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe)
# 生成测试数据
test = np.array([[[9],[5],[2],[10]]]).astype('float32')
# 进行预测
results = infer_exe.run(inference_program,
feed={"x": test},
fetch_list=fetch_targets)
# 给出题目为 【9,5,2,10】 输出y=4*9+6*5+7*2+10*2的值
print ("9a+5b+2c+10d={}".format(results[0][0]))
利用神经网络改进Q-learning:DQN
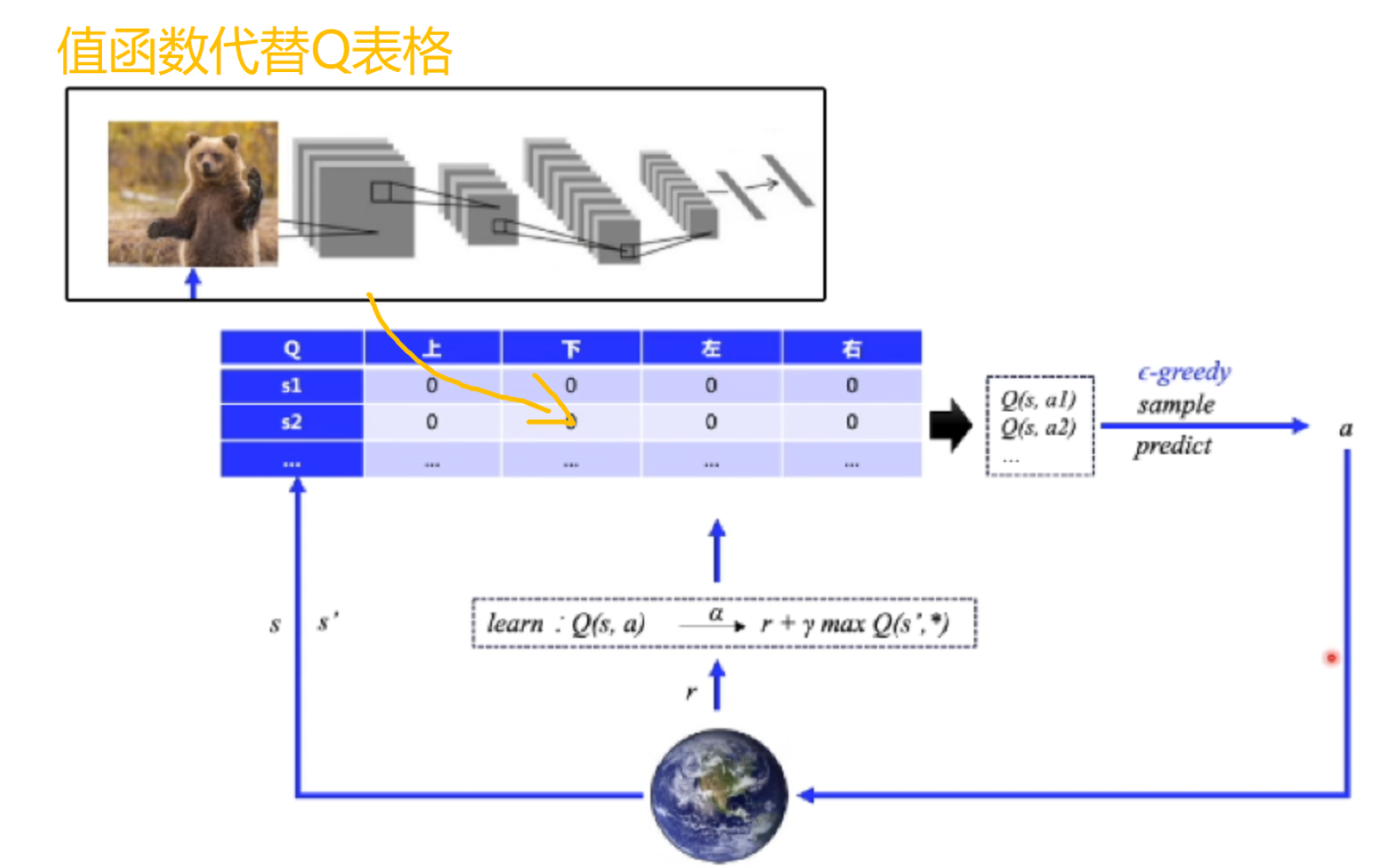
如上图所示,在Q-learning的基础上,将Q表格替换为神经网络所逼近的值函数,即为DQN算法。
DQN(approx)神经网络+Q-learning
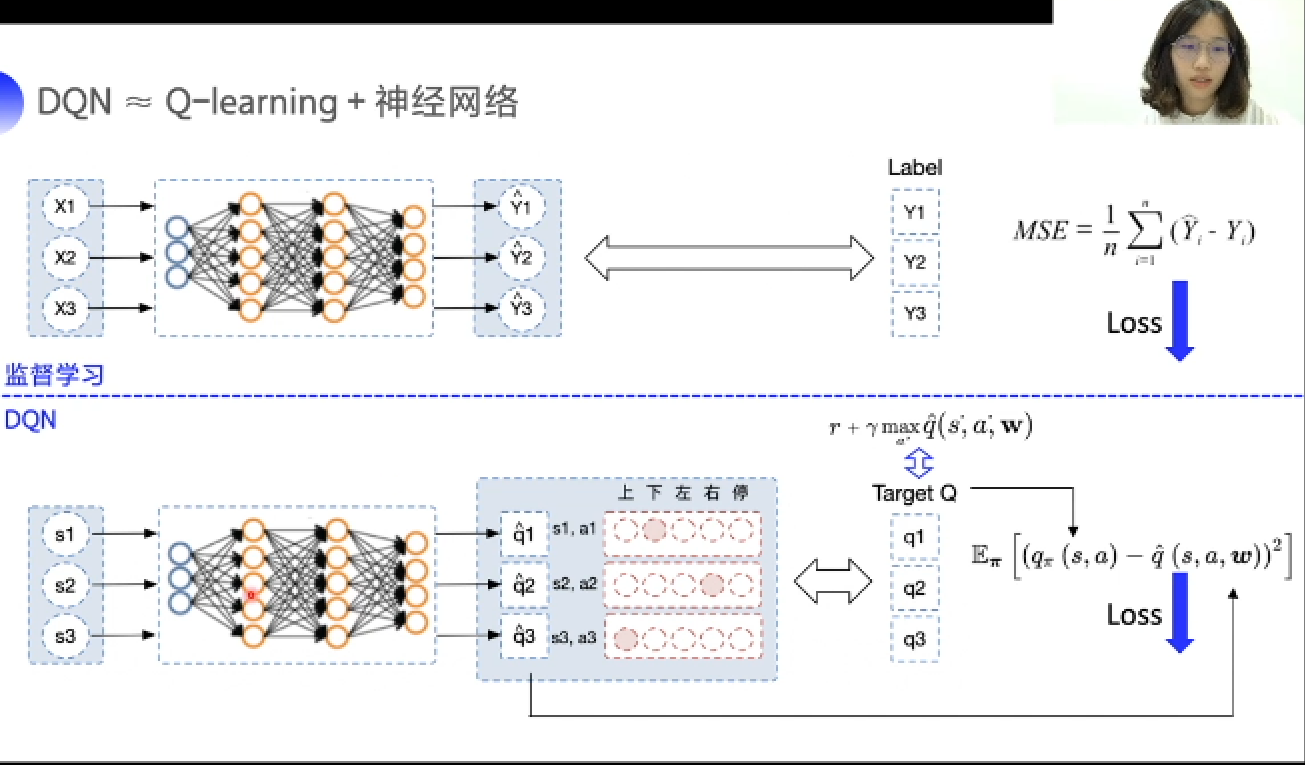
- 在监督学习中,误差由预测值与真实值得出,通过最小化误差来得到理想的模型;
- DQN与监督学习过程类似,误差由预测所得(q)矩阵与目标值(hat q)得出,通过最小化误差来逼近值函数。
2.DQN算法解析
由于DQN算法引入神经网络的同时也会引入非线性激活函数(例如,Relu),这样在理论上无法证明算法可以收敛。为了解决该问题,DQN提出两个创新点:1.经验回放;2.固定Q目标。
-
经验回放
-
存在的问题:由于强化学习中样本是时间上连续的一个决策序列,而神经网络输入的样本间应该相互独立。若按照时间顺序将样本进行训练则存在上述问题;同时,一条经验仅能使用一次,也存在样本利用率低的问题。
-
解决方法:经验回放
经验回放充分利用了off-policy的优势,通过设置一个经验池来存储behavior policy获得的若干条经验。将经验池内经验打乱,分成若干个小的经验块交给target policy训练,这样不但降低了降本间的关联性;同时还可以重复利用经验,提高了经验的利用率。

-
代码实现:
replay_memory.py
import random import collections import numpy as np class ReplayMemory(object): def __init__(self, max_size): self.buffer = collections.deque(maxlen=max_size) def append(self, exp): self.buffer.append(exp) def sample(self, batch_size): mini_batch = random.sample(self.buffer, batch_size) obs_batch, action_batch, reward_batch, next_obs_batch, done_batch = [], [], [], [], [] for experience in mini_batch: s, a, r, s_p, done = experience obs_batch.append(s) action_batch.append(a) reward_batch.append(r) next_obs_batch.append(s_p) done_batch.append(done) return np.array(obs_batch).astype('float32'), np.array(action_batch).astype('float32'), np.array(reward_batch).astype('float32'), np.array(next_obs_batch).astype('float32'), np.array(done_batch).astype('float32') def __len__(self): return len(self.buffer)
-
-
固定Q目标
-
存在的问题:由于监督学习中,标签值确定,因此,算法是平稳的。但在DQN中,需要逼近的target Q也是不断变化的,会给影响算法效果。
-
解决方法:固定Q目标。
在一段时间内固定产生target Q的模型,这段时间内只逼近固定的target Q。从而改善算法的平稳性。
-
1. DQN算法流程图&PARL框架
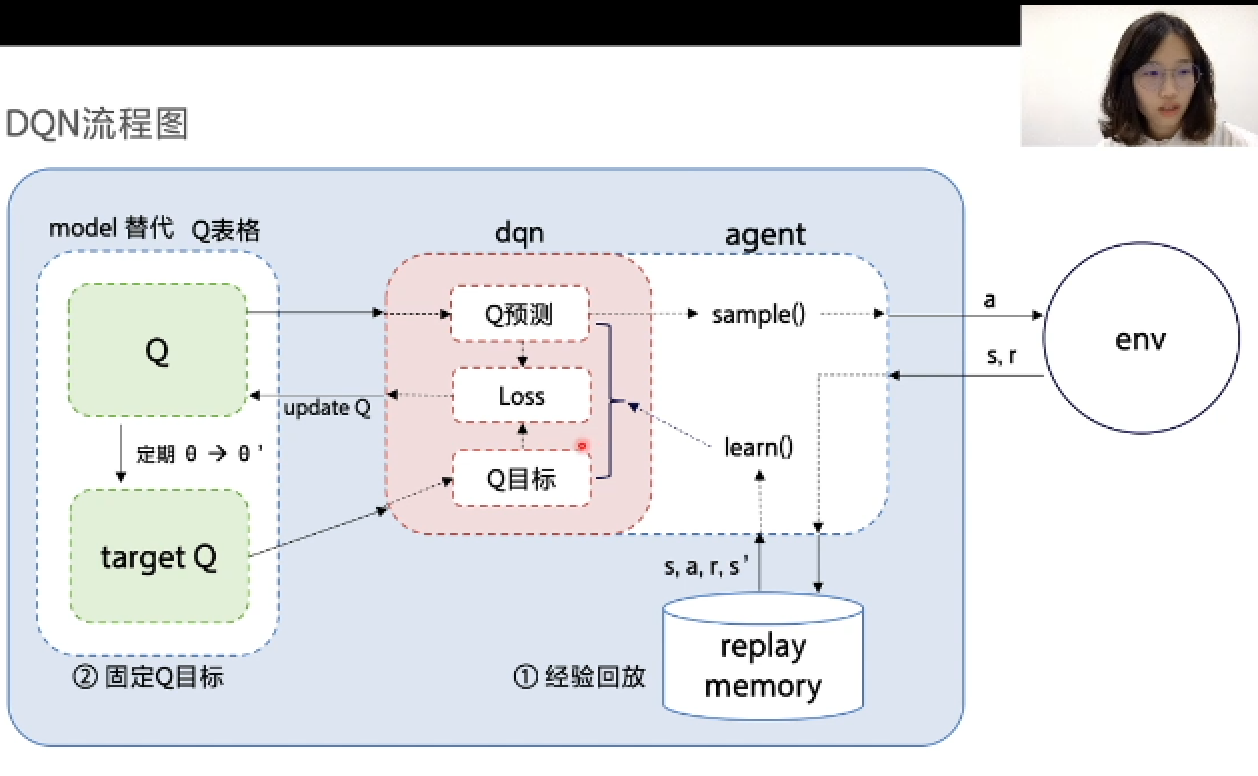
DQN算法流程图如上图所示:智能体(agent)与环境交互获得经验,并将经验存入经验池内。用Q模型代替Q表格,同时定期复制Q模型参数来更新target Q模型。通过计算Q预测与Q目标的误差来更新Q模型。其中更新Q模型的红色部分,为DQN算法的核心。
按照上述算法框架,PARL将强化学习抽象为:模型(model)、算法(algorithm)、智能体(agent)三部分。如下图所示,Model来定义网络结构,Algorithm来定义具体的算法来更新网络结构,Agent负责算法与环境的交互,交互的过程中将经验提供给算法去更新模型。

-
代码实现
1. model.py
model.py定义了一个Model的功能类,首先定义网络结构,之后调用value(obs)方法,输入状态,输出q值。
#-*- coding: utf-8 -*- import parl from parl import layers # 封装了 paddle.fluid.layers 的API class Model(parl.Model): def __init__(self, act_dim): hid1_size = 128 hid2_size = 128 # 3层全连接网络 self.fc1 = layers.fc(size=hid1_size, act='relu') self.fc2 = layers.fc(size=hid2_size, act='relu') self.fc3 = layers.fc(size=act_dim, act=None) def value(self, obs): h1 = self.fc1(obs) h2 = self.fc2(h1) Q = self.fc3(h2) return Q2. algorithm.py
#-*- coding: utf-8 -*- import copy import paddle.fluid as fluid import parl from parl import layers class DQN(parl.Algorithm): def __init__(self, model, act_dim=None, gamma=None, lr=None): """ DQN algorithm Args: model (parl.Model): 定义Q函数的前向网络结构 act_dim (int): action空间的维度,即有几个action gamma (float): reward的衰减因子 lr (float): learning_rate,学习率. """ self.model = model self.target_model = copy.deepcopy(model) assert isinstance(act_dim, int) assert isinstance(gamma, float) assert isinstance(lr, float) self.act_dim = act_dim self.gamma = gamma self.lr = lr def predict(self, obs): """ 使用self.model的value网络来获取 [Q(s,a1),Q(s,a2),...] """ return self.model.value(obs) def learn(self, obs, action, reward, next_obs, terminal): """ 使用DQN算法更新self.model的value网络 """ # 从target_model中获取 max Q' 的值,用于计算target_Q next_pred_value = self.target_model.value(next_obs) best_v = layers.reduce_max(next_pred_value, dim=1) best_v.stop_gradient = True # 阻止梯度传递 terminal = layers.cast(terminal, dtype='float32') target = reward + (1.0 - terminal) * self.gamma * best_v pred_value = self.predict(obs) # 获取Q预测值 # 将action转onehot向量,比如:3 => [0,0,0,1,0] action_onehot = layers.one_hot(action, self.act_dim) action_onehot = layers.cast(action_onehot, dtype='float32') # 下面一行是逐元素相乘,拿到action对应的 Q(s,a) # 比如:pred_value = [[2.3, 5.7, 1.2, 3.9, 1.4]], action_onehot = [[0,0,0,1,0]] # ==> pred_action_value = [[3.9]] pred_action_value = layers.reduce_sum( layers.elementwise_mul(action_onehot, pred_value), dim=1) # 计算 Q(s,a) 与 target_Q的均方差,得到loss cost = layers.square_error_cost(pred_action_value, target) cost = layers.reduce_mean(cost) optimizer = fluid.optimizer.Adam(learning_rate=self.lr) # 使用Adam优化器 optimizer.minimize(cost) return cost def sync_target(self): """ 把 self.model 的模型参数值同步到 self.target_model """ self.model.sync_weights_to(self.target_model)3. agent.py
import numpy as np import paddle.fluid as fluid import parl from parl import layers class Agent(parl.Agent): def __init__(self, algorithm, obs_dim, act_dim, e_greed=0.1, e_greed_decrement=0): assert isinstance(obs_dim, int) assert isinstance(act_dim, int) self.obs_dim = obs_dim self.act_dim = act_dim super(Agent, self).__init__(algorithm) self.global_step = 0 self.update_target_steps = 200 # 每隔200个training steps再把model的参数复制到target_model中 self.e_greed = e_greed # 有一定概率随机选取动作,探索 self.e_greed_decrement = e_greed_decrement # 随着训练逐步收敛,探索的程度慢慢降低 def build_program(self): '''Note: | Users **must** implement this function in an ``Agent``. | This function will be called automatically in the initialization function.''' # 定义agent计算图 # pred_program 为预测的计算图 self.pred_program = fluid.Program() # learn_program 为更新Q值函数的计算图 self.learn_program = fluid.Program() # 定义pred_program计算图的过程:定义输入与输出 with fluid.program_guard(self.pred_program): # 搭建计算图用于 预测动作,定义输入输出变量 # ----------------------定义输入---------------------------------- obs = layers.data( name='obs', shape=[self.obs_dim], dtype='float32') # ----------------------定义输出---------------------------------- self.value = self.alg.predict(obs) with fluid.program_guard(self.learn_program): # 搭建计算图用于 更新Q网络,定义输入输出变量 # ----------------------定义输入---------------------------------- obs = layers.data( name='obs', shape=[self.obs_dim], dtype='float32') action = layers.data(name='act', shape=[1], dtype='int32') reward = layers.data(name='reward', shape=[], dtype='float32') next_obs = layers.data( name='next_obs', shape=[self.obs_dim], dtype='float32') terminal = layers.data(name='terminal', shape=[], dtype='bool') # ----------------------定义输出---------------------------------- self.cost = self.alg.learn(obs, action, reward, next_obs, terminal) def sample(self, obs): sample = np.random.rand() # 产生0~1之间的小数 if sample < self.e_greed: act = np.random.randint(self.act_dim) # 探索:每个动作都有概率被选择 else: act = self.predict(obs) # 选择最优动作 self.e_greed = max( 0.01, self.e_greed - self.e_greed_decrement) # 随着训练逐步收敛,探索的程度慢慢降低 return act def predict(self, obs): # 选择最优动作 obs = np.expand_dims(obs, axis=0) pred_Q = self.fluid_executor.run( self.pred_program, feed={'obs': obs.astype('float32')}, fetch_list=[self.value])[0] pred_Q = np.squeeze(pred_Q, axis=0) act = np.argmax(pred_Q) # 选择Q最大的下标,即对应的动作 return act def learn(self, obs, act, reward, next_obs, terminal): # 每隔200个training steps同步一次model和target_model的参数 if self.global_step % self.update_target_steps == 0: self.alg.sync_target() self.global_step += 1 act = np.expand_dims(act, -1) feed = { 'obs': obs.astype('float32'), 'act': act.astype('int32'), 'reward': reward, 'next_obs': next_obs.astype('float32'), 'terminal': terminal } cost = self.fluid_executor.run( self.learn_program, feed=feed, fetch_list=[self.cost])[0] # 训练一次网络 return cost
2. 文件间调用关系

3.总结
