ch1绪论
数据结构基本知识:1.散列存储:根据元素的关键字直接计算出该元素的存储地址;2.顺序存储(逻辑上相邻且物理上也相邻)和链接存储(逻辑上相邻但物理上不相邻);3.索引存储(有索引表,检索速度快,但占空间)2.时间复杂度指的是在最坏的情况下的;3.空间复杂度(原地工作指的是空间复杂度为O(1))。

ch2线性表
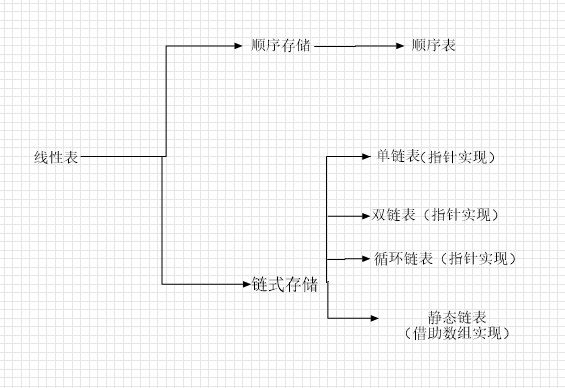
顺序表删除某个元素、插入某个元素、按值查找的最坏情况下,时间复杂度是O(n)。
链表中删除、插入不需要移动很多元素,只要修改相应的指针即可,但是查找某个元素的话时间复杂度是O(n)。
ch3栈和队列
栈后进先出,只允许在一端(栈顶)进行操作(插入和删除);根据存储结构分成顺序栈和链式栈;应用:在括号匹配中的应用、表达式求值(后缀表达式)、递归。
队列先进先出,在队尾进行插入,在对头删除;根据存储结构分成顺序队列(如:循环队列)和链式队列(如:双端队列);应用:层次遍历。
数组,多维数组(两种映射方法:按行优先和按列优先)。
矩阵,矩阵的压缩存储,稀疏矩阵。
ch4树和二叉树
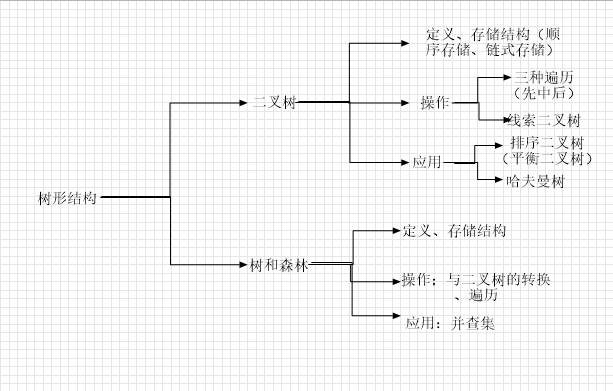
1.树:祖先结点、子孙结点;双亲结点(最接近)、孩子结点、兄弟结点(同双亲);分支结点(度大于0的结点也称为非终端结点)、叶子结点(度为0的结点也称为终端结点);有序树和无序树。
2.二叉树与度为2的有序树的区别:1)度为2的树至少有3个结点,而二叉树可以为空;2)二叉树需要确定左右次序。
3.二叉树的存储结构有顺序存储(一般用于满二叉树和完全二叉树)、链式存储(用链表来存储每个树结点)。
4.遍历:先序遍历(NLR)、中序遍历(LNR)、后序遍历(LRN)【序指的是根结点在何时被访问】、层次遍历(使用队列)。只知道先序遍历和后序遍历的序列不能唯一一颗二叉树。
5.线索二叉树:线索二叉树的引入是为了加快查找结点前驱和后继的速度(传统的链式存储仅能体现一种父子关系,不能直接得到结点在遍历中的前驱或后继);以这种结点结构(ltag,lchild,data,rtag,rchild)构成的二叉链表作为二叉树的存储结构,叫线索链表,其中指向结点前驱和后继的指针,叫做线索,加上线索的二叉树叫做线索二叉树,对二叉树以某种次序遍历使其变为线索二叉树的过程称为线索化。
线索二叉树的构造,就是遍历一次二叉树,检查当前结点左、右指针域是否为空,若为空,将他们改为指向前驱结点或后继结点的线索。
6.树、二叉树、森林的转换
树->二叉树:每个结点左指针指向它的第一个孩子结点,右指针指向它在树中的相邻结点。
二叉树->森林:二叉树根的右子树可以看作是一个除第一棵树外的森林转换后的二叉树。
森林->二叉树:森林先转换为树,树再转换为二叉树。
7.树的遍历
树的先根遍历,访问顺序与这棵树相应二叉树的先序遍历顺序相同;树的后根遍历,访问顺序与这棵树相应二叉树的中序遍历顺序相同。
8.二叉排序树(BST又称为二叉查找树)
L(左子树的结点值)<N(根结点值)<R(右子树的结点值)
9.平衡二叉树(AVL)
AVL(左、右子树的绝对值不超过1)的插入(LL、RR、LR、RL)
10.哈夫曼(Huffman)WPL最小