皮尔逊相关系数与斯皮尔曼秩[转载]

转自：https://www.zhihu.com/question/19734616/answer/349132554

https://www.cnblogs.com/zhangchaoyang/articles/2631907.html

1.Pearson

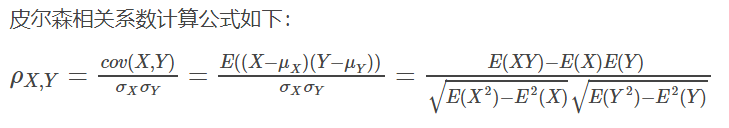
 分母是两个变量的标准差，分子是协方差。

 对于居中的数据来说（何谓居中？也就是每个数据减去样本均值，居中后它们的平均值就为0），E(X)=E(Y)=0，此时有：

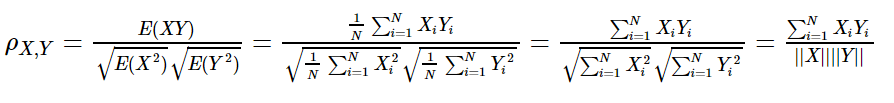
即相关系数可以看作是两个随机变量中得到的样本集向量之间夹角的cosine函数。

进一步当X和Y向量归一化后，||X||=||Y||=1，相关系数即为两个向量的乘积

这就是它的几何意义。

2.Spearman

spearman秩相关系数是一种无参数（与分布无关）检验方法，用于度量变量之间联系的强弱。（只是单调关系，并不一定是线性的）

在没有重复数据的情况下，如果一个变量是另外一个变量的严格单调函数，则Spearman秩相关系数就是+1或-1，称变量完全Spearman秩相关。注意这和Pearson完全相关的区别，只有当两变量存在线性关系时，Pearson相关系数才为+1或-1。

对原始数据x_i,y_i按从大到小排序，记x'_i,y'_i为原始x_i,y_i在排序后列表中的位置，x'_i,y'_i称为x_i,y_i的秩次，秩次差d_i=x'_i-y'_i。Spearman秩相关系数为：

3.Spearman实例

位置	原始X	排序后	秩次	原始Y	排序后	秩次	秩次差
1	12	546	5	1	78	6	1
2	546	45	1	78	46	1	0
3	13	32	4	2	45	5	1
4	45	13	2	46	6	2	0
5	32	12	3	6	2	4	1
6	2	2	6	45	1	3	-3

对于上表数据，算出Spearman秩相关系数为：1-6*(1+1+1+9)/(6*35)=0.6571

查阅秩相关系数检验的临界值表

n	显著水平
	0.05	0.01
5	0.9	1
6	0.829	0.943
7	0.714	0.893

置信度=1-显著水平。上表显示在n=6的时候，当spearman秩相关系数>=0.829时我们有95%的置信度认为两个随机变量相关，当spearman秩相关系数>=0.943时我们有99%的置信度认为两个随机变量相关。由于0.6571<0.829，即置信度达不到95%，所以我们不能认为X和Y相关。

如果原始数据中有重复值，则在求秩次时要以它们的平均值为准，比如：

原始X	秩次	调整后的秩次
0.8	5	5
1.2	4	(4+3)/2=3.5
1.2	3	(4+3)/2=3.5
2.3	2	2
18	1	1

Spearman秩相关系数应该是从秩和检验延伸过来的，因为它们很像。

 4.相关性和相似度的区别

X=(1,2,3)跟Y=(4,5,6)的皮尔森相关系数等于1，说明X和Y是严格线性相关的（事实上Y=X+3）。

但是X和Y的相似度却不是1，如果用余弦距离来度量相似度，X和Y之间的距离明显大于0。

5.Pearson局限性

2021-5-26更新——————————

6.在python中的计算方法

https://blog.csdn.net/u011412768/article/details/86714540

from scipy import stats
import numpy as np
 
a = np.array([0, 0, 0, 1, 1, 1, 1])
b = np.arange(7)
s1 = stats.pearsonr(a, b)
 
s2 = stats.pearsonr([1,2,3,4,5], [5,6,7,8,7])
print("s1:", s1)
print("s2:", s2)

输出：

s1: (0.8660254037844387, 0.011724811003954626)
s2: (0.8320502943378438, 0.08050957329849848)

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.pearsonr.html

返回的结果是：【相关性值，p-value】