力扣215题215. 数组中的第K个最大元素应用了。
1.预备知识-完全二叉树
https://zhuanlan.zhihu.com/p/153216919
名称与二叉树的存储结构有关,顺序存储:
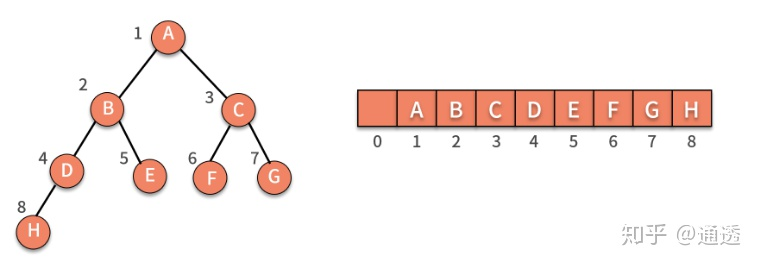
完全二叉树在顺序存储的时候,只浪费了一个空间,而且根节点和左右子节点之间存在着线性映射的关系。
而下图中非完全二叉树就会浪费很多空间:
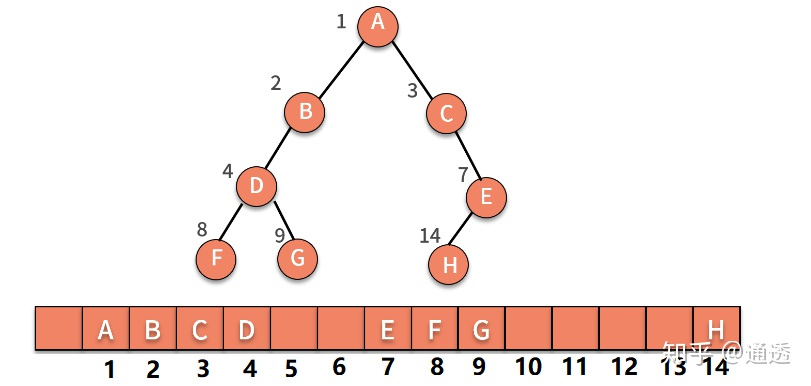
2.完全二叉树的下标关系
https://www.cnblogs.com/harrymore/p/9121886.html
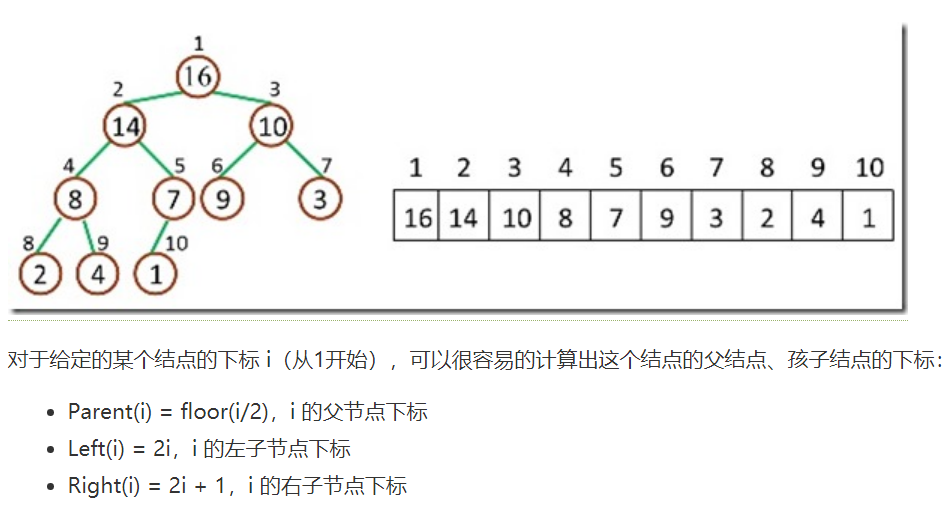
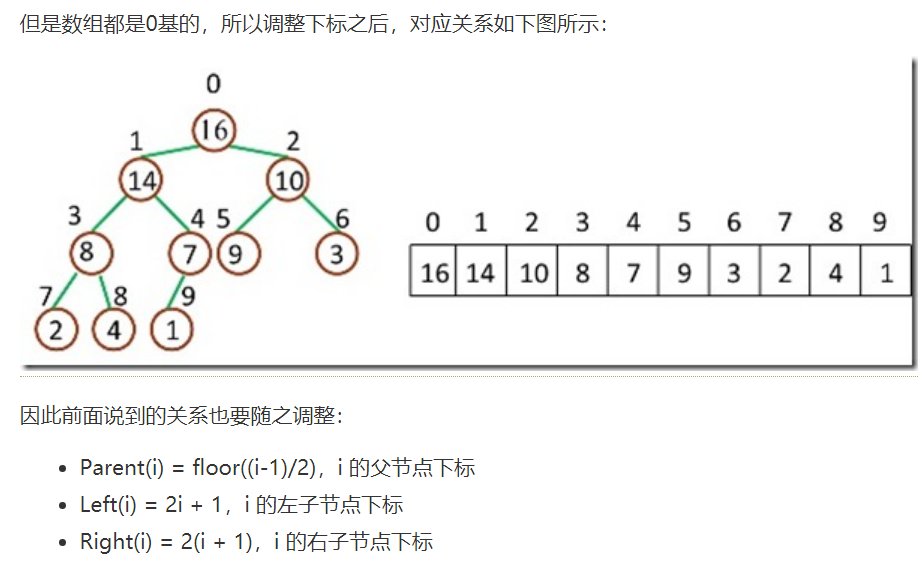
堆排序中是按照数组从0开始实现的。
3.堆排序
3.1构建初始堆
基本过程:从最后一个非叶子节点开始,选取子结点中最大的数,判断是否和根节点交换,逐级向上,形成最大堆。
https://songlee24.github.io/2014/04/02/heap-sort-implementation/
void BuildMaxHeap(ElementType A[], int len) { for(int i=len/2-1; i>=0; --i) // 从i=n/2-1到0,反复调整堆 AdjustDown(A, i, len); }
n个结点的完全二叉树中,最后一个结点是第n/2(向下取整)个结点的孩子。完全二叉树中非叶子节点和叶子结点的数量相等。
对第n/2(向下取整)个结点为根的子树进行筛选(以大根堆为例,若根结点的关键字小于左右子女中关键字的较大者,则交换),使该子树成为堆。之后向前依次对从n/2-1到1的各结点为根的子树进行筛选,看该结点值是否大于其左右子结点的值,若不是,将左右子结点中较大值与之交换,交换后可能会破坏下一级的堆,(这里的下一级指的是父节点往上的堆,更大一个层次的堆),于是继续采用上述方法构造下一级的堆,直到以该结点为根的子树构成堆为止。反复利用上述调整堆的方法建堆,直到根结点。
调整以i为根节点的子树成堆:
void AdjustDown(ElementType A[], int i, int len) { ElementType temp = A[i]; // 暂存A[i] for(int largest=2*i+1; largest<len; largest=2*largest+1)//向较大值的那个子树更新 { if(largest!=len-1 && A[largest+1]>A[largest]) ++largest; // 如果右子结点大 if(temp < A[largest]) { A[i] = A[largest]; i = largest; // 记录交换后的位置 } else break; } A[i] = temp; // 被筛选结点的值放入最终位置 }
在for循环中为什么largest=2*largest+1呢?因为largest指向的是左右子树中的较大值,那么把较大的值和根节点交换,是不影响另一个子树的堆性质的,因为交换后根节点比它的根节点要大!影响的只有被交换的子树的堆性质,所以只需要调整交换的子树即可。
3.2 堆排序
在删除的过程中,删除根节点,之后最后一个元素补上,再进行排序的调整。
void HeapSort(ElementType A[], int n) { BuildMaxHeap(A, n); // 初始建堆 for(int i=n-1; i>0; --i) // n-1趟的交换和建堆过程 { // 输出最大的堆顶元素(和堆底元素交换) A[0] = A[0]^A[i];//不太明白为什么不用swap??? A[i] = A[0]^A[i]; A[0] = A[0]^A[i]; // 调整,把剩余的n-1个元素整理成堆 AdjustDown(A, 0, i); } }
也就是交换堆底与堆顶元素,再调整堆。
3.3 图示过程
https://www.cnblogs.com/chengxiao/p/6129630.html
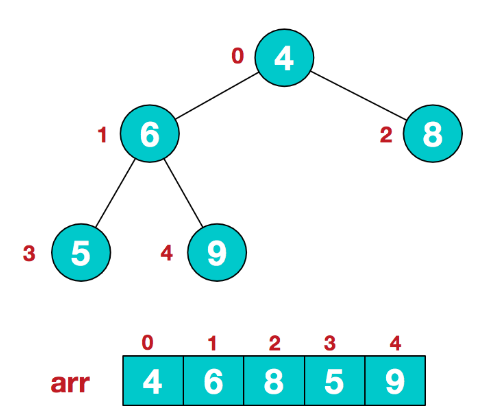
刚初始化时
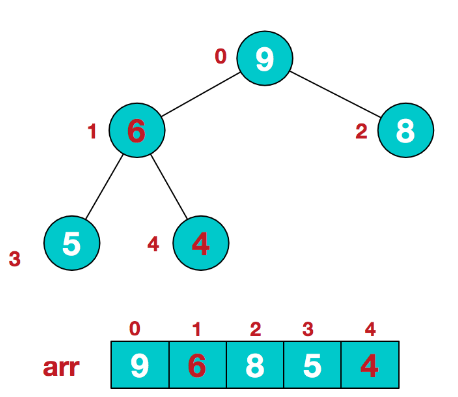
初始建堆完成-大顶堆
可以发现经过步骤一初始建堆完成之后,形成了大顶堆,但是数组中并不是递增排序的,还需要进行步骤二调整。将最大元素与最后的元素交换,并且堆的大小-1,最终调整结果如下:
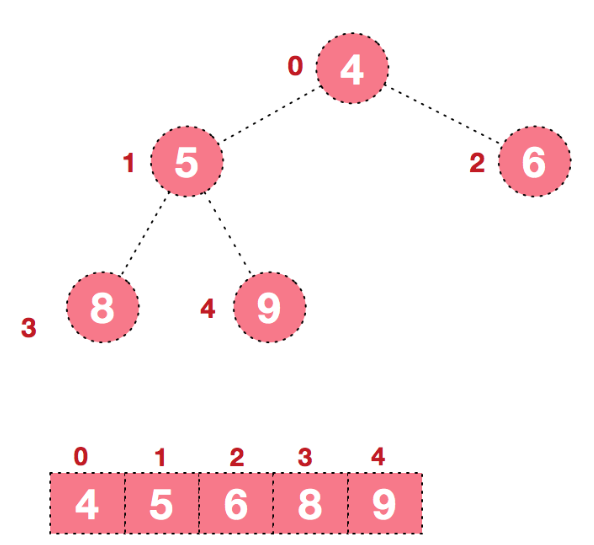
最终堆排序的结果反倒是形成了一个小顶堆。
4.性能
时间复杂度:O(nlogn),n表示树的节点个数,建堆时,对每个父节点都有一次调整的过程,每次调整的复杂度为O(logn),所以总的是。
空间复杂度:仅使用了常数个辅助单元,空间复杂度为O(1)。
稳定性:堆排序是不稳定的算法,它不满足稳定算法的定义。它在交换数据的时候,是比较父结点和子节点之间的数据,所以,即便是存在两个数值相等的兄弟节点,它们的相对顺序在排序也可能发生变化。
5.手写堆排序
void adjust(vector<int>& nums,int i,int r){//这里的r是开区间 int temp=nums[i]; for(int j=2*i+1;j<r;j=2*j+1){//其实这里不应该有=,=的话说明是最后一个节点了,没有子节点,不需要调整 if(j+1<r&&nums[j+1]>nums[j])j++;//原来是这里写错了 。//这里要判断j+1<r,是开区间开区间开区间 //if(nums[j]>nums[i]){//这里不应该和nums[i]比较,因为它可能已经被赋了更大的值,应该和temp比 //此次就是为了给temp找到合适的位置。 if(nums[j]>temp){ nums[i]=nums[j]; i=j;//因为j把i给覆盖掉了,i目前就要暂定放在j的位置了 }else break;//说明已经成堆,不必往下检查了 } nums[i]=temp; } int main(){ //vector<int> nums={10,1,35,61,89,36,55}; //vector<int> nums={29,25,3,49,9,37,21,43}; vector<int> nums={1,9,8,2,10,7,3}; //首先建立大顶堆,然后依次调整每个堆顶元素 int n=nums.size(); for(int i=n/2-1;i>=0;i--)//调整以i为根节点的堆 adjust(nums,i,n);//控制堆的大小
for(int i=n-1;i>=0;i--){//这里倒着遍历,可以通过i来控制当前堆的大小 swap(nums[0],nums[i]); adjust(nums,0,i); } return 0; }
遇到的问题:
参数分别为:数组,起始调整点,总元素数目。