101 Hack 50 闲来无事。也静不下心,打个代码压压压惊
Hard Questions
Vincent and Catherine are classmates who just took an exam in Math 55. The exam consists of multiple-choice questions. Each question has choices, each of which is represented by a single capital letter A, B, C, D and E. Each question has exactly one correct answer. A student's score is equal to the number of questions he/she correctly answered.
This was the hardest exam they've ever taken! No one was ever sure of their answer even after the exam, and some students weren't even able to answer all the questions. The questions were so hard that Vincent and Catherine strongly believe that they can't both be correct in any question. In other words, for each question, they believe that one or both of them must be incorrect.
Now, Vincent wants to know how well he could have performed in the exam. Given the answers of Vincent and Catherine, find the maximum score that Vincent could have gotten, assuming that they can't both have gotten the correct answer to any particular question.
Input Format
The first line contains a single integer , the number of questions.
The second line contains a string of length denoting the answers of Vincent.
The third line contains a string of length denoting the answers of Catherine.
Each answer string consists of only the characters A, B, C, D, E and . (dot character).
- If the 'th character is
A,B,C,DorE, then this character represents the student's answer for the 'th question. - If the 'th character is
., then this means the student gave no answer for the 'th question.
Constraints
Output Format
Print a single line containing a single integer denoting the maximum score that Vincent could have gotten assuming that they can't both have gotten the correct answer to any particular question.
Sample Input 0
24
CCACCBAEBAAAAAAAA.......
CCACCBAEBAAAAAAAA.......
Sample Output 0
0
Explanation 0
In this case, Vincent and Catherine answered exactly the same for the whole exam. Since they can't both be correct in any question, it means they are both incorrect in every question. Hence, they both score .
Sample Input 1
7
ACCEDED
DECADE.
Sample Output 1
4
Explanation 1
In this case, the answer sheet could have been ACBEABD, in which Vincent scores . However, one can also show that Vincent cannot get a higher score than assuming Vincent and Catherine can't both be correct in any question. Hence, the answer is .
The following diagram illustrates this case:
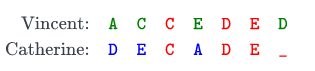
Sample Input 2
11
BEE..ADDED.
CAB.DAD.DEE
Sample Output 2
6
Explanation 2
In this case, the answer sheet could have been BEEADEBDEDE, in which Vincent scores . However, one can also show that Vincent cannot get a higher score than assuming Vincent and Catherine can't both be correct in any question. Hence, the answer is .
The following diagram illustrates this case:



