前置知识
期望的线性性
第一个性质是期望的可加性:
第二个性质是当随机变量 (X) 和 (Y) 独立时:
条件概率
在 (B) 成立的前提下 (A) 成立的概率等于 (AB) 同时成立的概率除以 (B) 成立的概率:
贝叶斯公式同理:
(%)$$P(A|B)=frac{P(B|A)P(A)}{P(B)}$$
方差相关
概率生成函数
对于任意取值在非负整数集上的离散随机变量 (X),他的概率生成函数为:
一些性质:
Game on Tree
题目描述
解法
可以考虑每个点对期望操作次数的贡献,一个点期望产生 (1) 的贡献,当且仅当它比它的祖先先被染色,这样的概率是 (frac{1}{dep_i}),所以每个点贡献的期望是 (frac{1}{dep_i})
那么根据期望的线性性,答案就是 (sum frac{1}{dep_i})
Forest game
题目描述
给定一棵 (n) 个节点的树,每次等概率选择一个点,删去它和所有和它相连的边,得分记为这个连通块大小,总得分为每次操作得分之和,求总得分的期望。
(nleq 100000)
解法
好像每次的得分是连通块大小,这个贡献好像不是很好算。考虑把它拆成更小的贡献 ,考虑删去 (u) 点时 (v) 点对它有没有贡献,当且仅当 (u) 是 ((u,v)) 路径上第一个被删去的节点,期望是 (frac{1}{dis(u,v)+1})
根据期望的线性性,答案是 (sum_usum_vfrac{1}{dis(u,v)+1})
这种树上路径问题就可以考虑点分治,但是这个题要把每个距离有多少个给算出来。对于分治中心,考虑每个子树的生成函数,我们把它们暴力求卷积即可,再减去子树内部自己的卷积就可以了。时间复杂度 (O(nlog^2 n)),( t FFT) 要打递归版本的。
#include <cstdio>
#include <iostream>
#include <cmath>
using namespace std;
const int M = 400005;
const int p = 1e9+7;
const double pi = acos(-1.0);
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,tot,len,up,rt,ans,sz;
int f[M],siz[M],mx[M],vis[M],rev[M];
struct edge
{
int v,next;
edge(int V=0,int N=0) : v(V) , next(N) {}
}e[2*M];
struct complex
{
double x,y;
complex() {}
complex(double X,double Y) : x(X) , y(Y) {}
complex operator + (const complex &R) const {return complex(x+R.x,y+R.y);}
complex operator - (const complex &R) const {return complex(x-R.x,y-R.y);}
complex operator * (const complex &R) const {return complex(x*R.x-y*R.y,x*R.y+y*R.x);}
}a[M];
void FFT(complex *a,int len,int fl)
{
for(int i=0;i<len;i++)
{
rev[i]=(rev[i>>1]>>1)|((i&1)*(len/2));
if(i<rev[i]) swap(a[i],a[rev[i]]);
}
for(int s=2;s<=len;s<<=1)
{
int t=s/2;complex w=complex(cos(2*pi/s),sin(2*pi/s)*fl);
for(int i=0;i<len;i+=s)
{
complex x=complex(1,0);
for(int j=0;j<t;j++,x=x*w)
{
complex fe=a[i+j],fo=a[i+j+t];
a[i+j]=fe+x*fo;
a[i+j+t]=fe-x*fo;
}
}
}
}
int jzm(int a,int b)
{
int r=1;
while(b>0)
{
if(b&1) r=1ll*r*a%p;
a=1ll*a*a%p;
b>>=1;
}
return r;
}
void find(int u,int fa,int sz)
{
siz[u]=1;mx[u]=0;
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa || vis[v]) continue;
find(v,u,sz);
siz[u]+=siz[v];
mx[u]=max(mx[u],siz[v]);
}
mx[u]=max(mx[u],sz-siz[u]);
if(mx[u]<mx[rt]) rt=u;
}
void dfs(int u,int fa,int d)
{
sz++;
a[d].x=a[d].x+1;up=max(up,d+1);
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa || vis[v]) continue;
dfs(v,u,d+1);
}
}
void work(int fl)
{
len=1;
while(len<2*up) len<<=1;
FFT(a,len,1);
for(int i=0;i<len;i++) a[i]=a[i]*a[i];
FFT(a,len,-1);
for(int i=0;i<len;i++)
{
ll tmp=(ll)(a[i].x/len+0.5);
tmp%=p;
ans=(ans+fl*tmp*jzm(i+1,p-2))%p;
a[i].x=a[i].y=0;
}
}
void solve(int u)
{
up=0;dfs(u,0,0);
work(1);
vis[u]=1;
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(vis[v]) continue;
up=sz=0;dfs(v,0,1);
work(-1);
rt=0;find(v,0,sz);
solve(rt);
}
}
signed main()
{
n=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
e[++tot]=edge(v,f[u]),f[u]=tot;
e[++tot]=edge(u,f[v]),f[v]=tot;
}
mx[0]=n;
find(1,0,n);
solve(rt);
ans=(ans+p)%p;
for(int i=1;i<=n;i++) ans=1ll*ans*i%p;
printf("%d
",ans);
}
[CTSC2017] 游戏
题目描述
解法
暴力 (dp) 是很容易的,但是如果要涉及到修改我们就束手无策了。考虑一些已知的比赛信息会把原序列划分成若干个段 ([i,j)),对于每个段的贡献是独立的,现在问题变成了算一段的贡献,可以考虑线段树维护之类的方法。
那么我们要维护的东西一定要是 支持快速合并的 ,并且还要 钦定两端的状态 ,分别维护概率和期望。设 (P_{i,j}(x,y)) 表示 (i) 局输赢状态 (x),(j) 局输赢状态 (y) 的概率,(E_{i,j}(x,y)) 表示 假定这种输赢状态为前提 下 ([i,j]) 赢得的期望场数,(pro[i][j][k]) 表示 (i-1) 轮状态是 (j),(i) 轮状态是 (k) 的概率(其实就是题目给的概率数组),那么有如下转移:
上面的式子很好理解,就是枚举中间的输赢情况是什么然后合并。
上面式子的本质其实是条件概率的一个应用:(E(A|B)=frac{E(AB)}{P(B)}),我们要求的是有假定前提的期望,但是分子算的是包含假定前提成立的期望,所以除以假定前提成立的概率就行,这里的假定前提就是 (i,j) 的输赢状态分别是 (x,y)
用线段树很容易维护上面那个东西,修改就维护一个 (set),找一下前驱后继随便改一改就行了。
矩形覆盖
题目描述
给定一个大小为 (n imes m) 的矩形,某一些格子上有物品,共有 (k) 个物品,现在等概率选一个子矩形,求子矩形内物品个数的方差期望。
(n,mleq 1e9,kleq 1e5)
解法
根据方差期望那套理论,我们分别求出 (E(x)) 和 (E(x^2)) 即可。
(E(x)) 比较好求,对于每一个点统计它的贡献,对于 ((x,y)) 有 (x imes (n-x+1) imes y imes(m-y+1))
(E(x^2)) 可以套路地考虑每一对点,统计包含它们的矩形的个数,可以考虑扫描线,分左上右下和右上左下两种情况讨论,然后离散化( t + BIT) 即可。相信你们都知道我的意思了
逃跑
题目描述
解法
还是求方差期望的题,按照套路我们将其转化为分别求 (E(x)) 和 (E(x^2))
先考虑怎么求 (E(x)),设 (f(i,j,k)) 表示第 (i) 秒第一次 移动 ((j,k)) 的概率,设 (g(i,j,k)) 表示第 (i) 秒 移动 ((j,k)) 的概率, 注意上面的定义位置是相对的 。对于 ((0,0)) 它的含义就变成了到达,所以答案是所有 (f(i,j,k)) 的和,(g) 可以较为容易地用 (dp) 求出。对于一个点 ((x,y)) 我们单独用生成函数算他的 (f):
那么满足下列关系式,含义就是花了时间不移动(注意相对的概念哦):
( t Therefore),(f) 可以在 (O(n^4)) 的时间复杂度内求得(可以写一个暴力多项式除法)
现在考虑 (E(x^2)) 怎么求,按照套路我们要对每一对点算贡献。考虑用 (dp) 处理,下面的操作就真的是艺高人胆大了,设 (h(i,j,k)) 表示第 (i) 秒第一次走到了 ((a+j,b+k)),之前已经到达了 ((a,b)),对于所有位置 ((a,b)) 的概率,显然把最后时刻所有位置的 (h) 求和就是答案。这个状态定义为什么牛逼呢?因为它省略了状态里需要枚举的 ((a,b)),但令人惊奇的是这样还能转移!
转移就先枚举 (a,b),再枚举一个时刻 (t),那我们就让它在 (t) 时刻第一次走到 ((a,b)),在剩下 (i-t) 时间内第一次走到 ((a+j,b+k))。但是这样显然会算错,因为可能在走到 ((a,b)) 的时候已经走到 ((a+j,b+k)) 了。枚举一个时刻 (t),(h(t,-j,-k)) 就是经过 ((a+j,b+k)) 第一次走到 ((a,b)) 的方案,然后再第一次走到 ((a+j,b+k))(这里的第一次指的是这次征程的第一次),那么汇总一下就这么转移:
前面那一项是个人就会优化,所以时间复杂度 (O(n^4))
[CTSC2006] 歌唱王国
题目描述
解法
这种题一般有套路的:列方程解生成函数 ,设 (f[i]) 表示结束时长度是 (i) 的概率,(g[i]) 表示长度是 (i) 还没有结束的概率,设 (F(x)) 为 (f[i]) 的生成函数,(G(x)) 为 (g[i]) 的生成函数,现在的任务是列出方程。
首先根据定义有:(f[i]=g[i-1]-g[i],f[0]=0,g[0]=1),那么可以推出 (F(x)=xG(x)-G(x)+1)
还要有一个方程才行,考虑 (f,g) 之间的联系,我们必须列一个方程来表示 (f,g) 之间的相互转化,考虑在 (g) 后面直接加入牛头人的名字 (A),设牛头人的名字长度是 (L),但是要考虑一种情况,就是没有加到 (L) 就已经合法了,但这时候 (f) 的后缀一定是 (A) 的一个 ( t border),建议结合图来理解这个方程怎么来的:
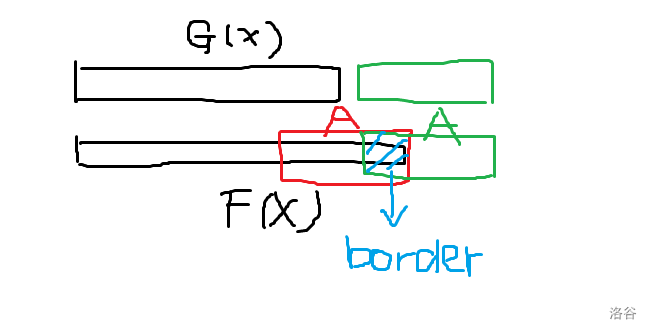
那么我们枚举 ( t border) 的长度 (i) 就可以写出下列方程,注意我们列的是生成函数的方程,但原理是根据单个项的等式关系来的,所以要注意 对齐项数 ,设 (a_i) 表示 ([1,i]) 是否是 (A) 的一个 ( t border):
剩下的问题就是解方程了,由于求的是结束时间的期望那么答案是 (F'(1)),我们先把第一个方程求导:
然后将 (x=1) 带入上面的式子:
那么问题变成了求 (G(1)),尝试用第二个式子把 (x=1) 带进去:
大功告成啦!所以代码还需要我给么
Dice
题目描述
有一个 (m) 面的骰子,求扔连续 (n) 次就相同就结束的期望部分和扔连续 (n) 次结果不同就结束的期望步数。
(n,mleq 1e6)
解法
解法只有一句话:照葫芦画瓢
第一问(注意第二个方程左边是一定成立的概率):
第二问:
如果你想从 (n-1) 来推也是可以的,只不过要注意去掉 (g_0) 那一项。
哥哥
懒得写了