判断两线段是否相交——快速排斥与跨立实验

　　如何判断两条线段是否相交呢？如果是我们去解决这个问题，用眼睛很容易就看出来了，但是如果用计算机来解决这个问题，该怎么办呢？下面介绍两个方法，这两个方法结合起来就能完美解决这个问题了。

 

一、快速排斥

对于两条线段，我们以这两条线段为对角线各自作一个矩形，如图所示，如果这两个矩形没有相交的部分那么这两条线段一定不相交，这样我们可以排除一部分不相交的情况了。

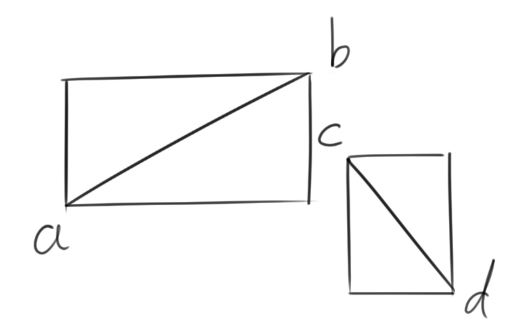
那么又该怎么判断这两个矩形是否相交呢？这就比判断线段要简单的多了，若：
·线段1下面的端点高于线段2上面的端点；
·线段1上面的端点低于线段2下面的端点；
·线段1左面的端点位于线段2右面的端点的右边；
·线段1右面的端点位于线段2左面的端点的左边；
那么我们就可以说这两个矩形不相交，即这两个线段不相交，用代码实现如下：

bool quick_judge(point a,point b,point c,point d)
{
    if(a.y>c.y||b.y<d.y||a.x>d.x||b.x<c.x)
        return false;
    else return true;
}

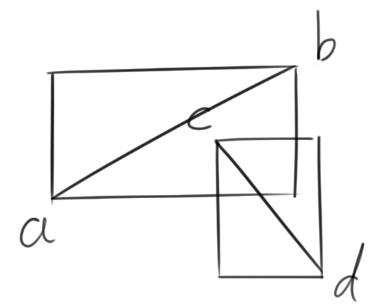
但是仅这一种判断方式无法解决我们的问题，有反例如下图，两矩形相交但是线段并没有相交，这就需要我们用第二种方法来加以辅助。

二、跨立实验

 

首先简单介绍一下向量的叉乘：

 

　　假设有两个二维向量a，b，那么它们的的叉乘结果为a×b=a.x*b.y-b.x*a.y，我们可以通过这个值得到很多有用的性质：
　　·a，b向量构成的平行四边形的面积。
　　·如果k>0时，那么a正旋转到b的角度为<180°，如果k<0，那么a正旋转到b的角度为>180°,如果k=0 那么a，b向量平行。

 

跨立实验用到的就是上面的第二个性质。

我们再来看跨立实验，简单来说，就是两条相交线段，其中一条的两个点一定在另一条的两边，如下图。

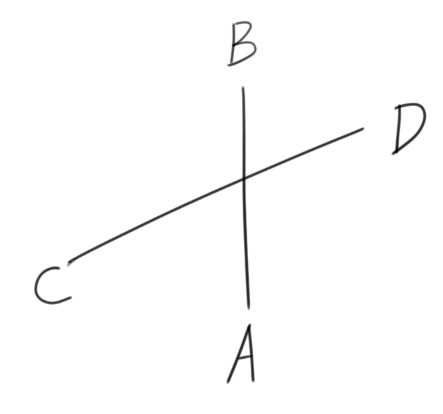
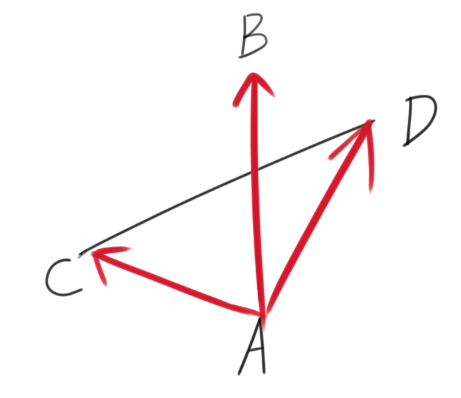
那么如何去判断呢，这就需要用到我们上面说到的叉乘了。如在下图中，我们选择线段AB为基准，然后去判断AC×AB与AD×AB是否是同向的，若不是同向的，则证明了B,D两点在线段AB的两边。即 

用代码来实现：

bool cross_judge(point a,point b,point c,point d)
{
    const double eps=1e-9;
    double ac,ad,cb,ca;
    ac=(c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x);
    ad=(d.x-a.x)*(b.y-a.y)-(d.y-a.y)*(b.x-a.x);
    ca=(a.x-c.x)*(d.y-c.y)-(a.y-c.y)*(d.x-c.x);    //保险起见，把另一条边也判断一下
    cb=(b.x-c.x)*(d.y-c.y)-(b.y-c.y)*(d.x-c.x);
    if(ac*ad<eps&&ca*cb<eps) return true;
    else return false;
}

至此，我们将这两个方法结合一下，就可以解决我们的问题了。

三、相关题目

 

1.例题 ZOJ P1648

#include <bits/stdc++.h>

using namespace std;

const double eps=1e-9;

struct segment
{
    double x1,x2,y1,y2;
}seg[2005];

bool judge(segment a,segment b)
{
    if(min(a.x1,a.x2)<max(b.x1,b.x2)&&max(a.x1,a.x2)>min(b.x1,b.x2)&&min(a.y1,a.y2)<max(b.y1,b.y2)&&max(a.y1,a.y2)>min(b.y1,b.y2))
    {
        double v1,v2,v3,v4;
        v1=(b.x1-a.x1)*(a.y2-a.y1)-(b.y1-a.y1)*(a.x2-a.x1);
        v2=(b.x2-a.x1)*(a.y2-a.y1)-(b.y2-a.y1)*(a.x2-a.x1);
        v3=(a.x1-b.x1)*(b.y2-b.y1)-(a.y1-b.y1)*(b.x2-b.x1);
        v4=(a.x2-b.x1)*(b.y2-b.y1)-(a.y2-b.y1)*(b.x2-b.x1);
        if(v1*v2<eps&&v3*v4<eps) return true;
        else return false;
    }
    else return false;
}

int main()
{
    int i,j,n,flag=0;
    while(~scanf("%d",&n))
    {
        flag=0;
        for(i=0;i<n;i++) scanf("%lf%lf%lf%lf",&seg[i].x1,&seg[i].y1,&seg[i].x2,&seg[i].y2);
        for(i=0;i<n;i++)
            for(j=i+1;j<n;j++)
            {
                if(judge(seg[i],seg[j]))
                {
                    flag=1;
                    break;
                }
            }
        if(flag) printf("burned!
");
        else printf("ok!
");
    }
    return 0;
}

 

Author : Houge　　Date : 2019.5.31

Update log :