一、离散状态的马尔科夫决策
1. 奖励因子r
在马尔科夫决策中,有个奖励因子r,在计算总期望价值的时候,奖励因子r的次方数会逐步增加。对于这个的解释可以理解为:今天的一元钱在明天一般都会贬值。所以当某个状态s较晚到达时,要控制奖励因子使得获得的价值减少。
2. Bellman方程
[V^{pi} = R(s) + gamma sum_{s^{'}epsilon S } P_{spi(s)}(s^{'})V^pi (s^{'})
]
假设有n个状态,则可以列出n个Bellman方程,且共含有n个未知量,那么就可以通过解这个线性方程组得到每个状态下对应的价值函数的值;
3. 值迭代
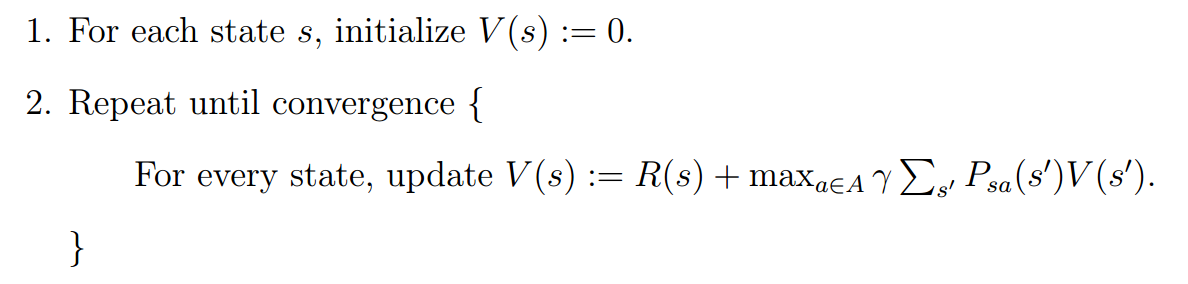
4. 政策迭代

5. 对比
假如状态有n个,政策迭代在计算时,需要计算含有n个方程和n个变量的方程组,当n≤1000时,政策迭代比较适用,当n>1000时,值迭代效率会更高。
因为在政策迭代中,需要求解Bellman方程,当状态数变多时,就需要求解同等数量的方程,这是一个相当大的计算负荷,因此此时使用值迭代会更好。
6. 转移概率和奖励因子的获取
在实际情况中,对于MDP的五元组,转移概率常常是未知的。我们可以通过统计在每个状态下打到某个状态的转移次数来得到近似的转移概率。此外,有时状态s1无法转移到状态s2,为了避免出现0除的情况,可以用 1 / |S|替代其概率。
if R is unknown, we can also pick our estimate of the expected immediate reward R(s) in state s to be the average reward observed in state s.
7. MDP求解全过程

二、连续状态的马尔可夫决策
对于连续型的状态,可以设定一定量的区间,使其离散化,将连续型的MDP变成离散型的MDP来解决。但是离散化通常而言表现都不是很好,数据分布的多样性被消除了,因此就无法学习到更深层次的数据的潜在信息。离散化还可能导致出现维数灾难。
1、拟合值迭代算法
