CodeForce 981F. Round Marriage

题目链接

https://codeforces.com/contest/981/problem/F

题意

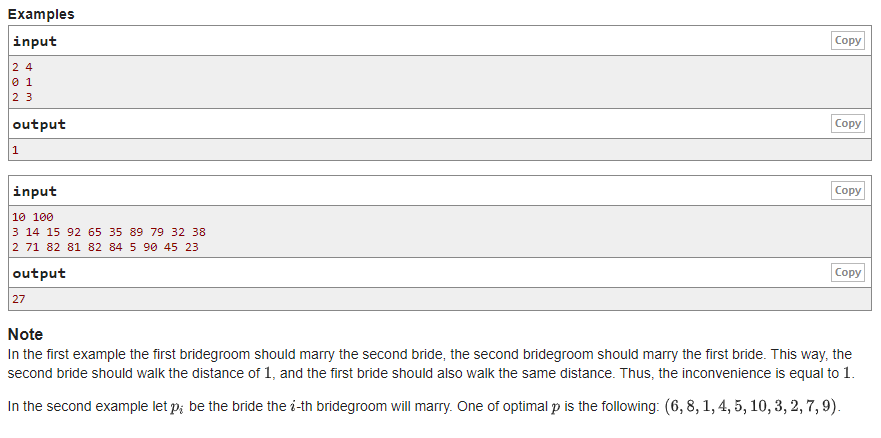
(n)个新郎和(n)个新娘围成一个环，长度为(L)，第(i)个新郎位置为(a_i),第(i)个新娘位置为(b_i),需要将他们两两配对，最小化新郎和新娘距离的最大值。

思路

考虑二分答案。
二分答案之后如何判定是否能完美匹配，(n)太大，可以用霍尔定理。
对于一个新郎 (i) ,可以找到的新娘为 ([L_i, R_i]),那么对于任意的(i, j),都有 (j - i >= R_j - L_i).
移项得 (L_i - i >= R_j - j) 那么不成立的条件便是 (L_i - i < R_j - j) 。
我们可以维护 (L_i - i)的最大值去判断是否存在$ R_j - j$ 大于他 如果存在即不合法。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 50;
ll a[maxn], b[maxn];
int n, L;
bool check(int mid){
    int mx = -0x3f3f3f3f3f3f;
    int l = 1, r = 1;
    for(int i = 1;i <= 2 * n;i++){
        while(l <= n * 4 && b[l] < a[i] - mid) l++;
        while(r <= n * 4 && b[r] <= a[i] + mid) r++;
        r--;
        mx = max(mx, l - i);
        if(r - i < mx) return false;
    }
    return true;
}
int main()
{
    std::ios::sync_with_stdio(false);
    cin >> n >> L;
    for(int i = 1;i <= n;i++) cin >> a[i];
    for(int i = 1;i <= n;i++) cin >> b[i];
    sort(a + 1, a + n + 1);
    sort(b + 1, b + n + 1);
    for(int i = 1;i <= n;i++) a[i] += L, a[n + i] = a[i] + L;
    for(int i = 1;i <= n * 3;i++) b[i + n] = b[i] + L;
    int l = 0, r = L / 2, ans = r;
    while(l <= r){
        int mid = l + r >> 1;
        if(check(mid)){
            r = mid - 1;
            ans = mid;
        }
        else l = mid + 1;
    }
    cout << ans << endl;
    return 0;
}