基本形式:
d个属性描述的示例x=(x1;x2;...;xd),xi是x在第i个属性上的取值。线性模型试图学一个通过属性的线性组合进行预测的函数:
f(x)=w1x1+w2x2+...+wdxd+b,
向量形式为
f(x)=wTx+b
w=(w1;w2;...;wd),w和b学得之后,模型可以确定。
非线性模型可以在线性模型基础上引入层级结构或高纬映射而得,此外w可以直观表达各属性在预测中农的重要性,有很好的解释性。
回归任务:
线性回归, 属性值间存在“序”的关系,则可以通过连续化将其转化为连续值,无“序”则可转化为向量。线性回归试图学得:
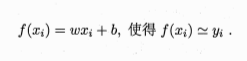
关键在于衡量f(x)与y之间的差别.其中,均方误差是回归任务中最常用的性能度量,可以试图让均方误差最小化:

几何意义:对应于常用的欧几里得距离“欧氏距离”,基于均方误差最小化来进行模型求解的方法称为“最小二乘法”,就是试图找到一条直线,使所有样本到直线上的欧式距离之和最小。
这个最小化的过程,称为线性回归模型的最小二乘"参数估计".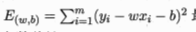
分别对w和b分别求导。
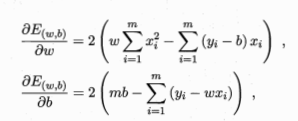
当都为0时,得到w和b最优解的闭式解
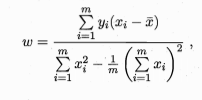
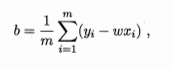

更一般的情形是如本节开头的数据集D,样本由d个属性描述,试图学得
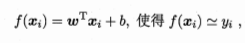 此为“多元线性回归”
此为“多元线性回归”
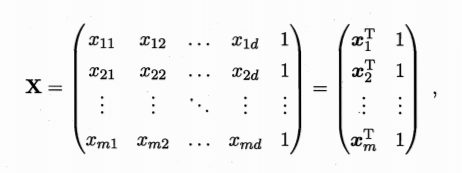
将标记写成向量形式y=(y1;y2;...;ym)有
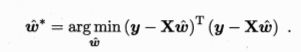
令 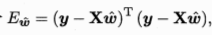 对 w求导得
对 w求导得
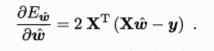
做一个简单的讨论当XTX为满秩矩阵或正定矩阵时,令求得的导为0得到多元最优解模型:

可以变换为ln y = wtx+b 此为“对数线性回归” 此为广义线性模型在g()=ln()时的特例
或者考虑到单调可微函数g(')
y=g-1(wtx+b)(广义线性模型)
3.3 对数几率回归
找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来,二分类问题:输出标记y为{0,1},线性回归模型产生的预测值z=wtx+b是实值
“单位阶跃函数”:
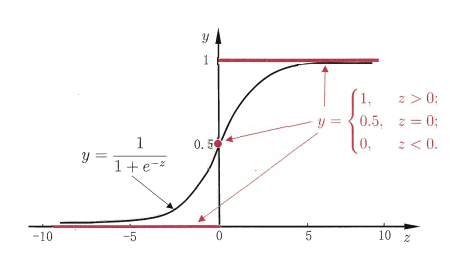
对数几率函数(logistic function):

y/1-y 称为“几率”,反映了x作为正例的相对可能性。对几率取对数则得到“对数几率”ln(y/1-y)
实际就是用线性回归模型的预测结果逼近真实标记的对数几率,因此,其对应的模型称为“对数几率回归”
接下来 确定式中的w和b,若将y视为后验概率估计p(y=1|x)则可重写为
lnp(y=1|x)/p(y=0|x) = wtx+b
显然 p(y=1|x) = ewtx+b/1+ewtx+b , p(y=0|x) = 1/1+ewtx+b
所以此处通过“极大似然法”(最大似然估计:现在已经拿到了很多个样本(你的数据集中所有因变量),这些样本值已经实现,最大似然估计就是去找到那个(组)参数估计值,使得前面已经实现的样本值发生概率最大。)
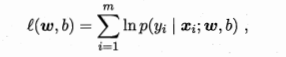
-->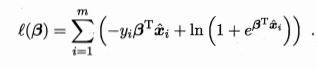
-->
-->更新公式 
-->一阶、二阶导数
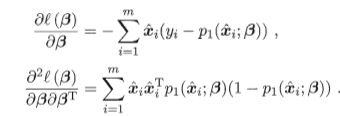
线性判别分析:大概什么原理,解决什么问题
线性判别分析:设法将样例投影到一条直线上,同类样例投影尽可能接近,异类样例尽可能远离。对新样本分类时,将其投影到同样的直线上,根据投影点的位置确定新样本的类别。本质是根据两者数据集的类间散度矩阵(均值向量相减相乘)、和两者协方差矩阵求类内散度矩阵进行相加。而多分类任务定义了“全局散度矩阵”为两类矩阵之和。类内散度矩阵重定义为每个类别的散度矩阵之和,则Sb为全局减去类内散度矩阵。
LDA可以用于多分类、也被视为一种经典的降维技术

多分类任务:
对问题进行拆分,为拆出的每个二分类任务训练一个分类器;在测试时,对分类器的预测结果进行集成以获得最终的多分类结果。
经典拆分有三种,1对1,1对多,多对多
类别不平衡的问题:
分类任务中不同类别的训练样例数目差别很大。分类器决策规则为:若y/1-y > 1 。预测为正例。 实际情况为 y/1-y > m+/m- 则预测为正例。
解决的三种办法:再缩放:欠采样、过采样、阈值移动