1418 抱歉 ACM 欧拉公式

题目：http://acm.hdu.edu.cn/showproblem.php?pid=1418

思路：一看题目，明显是要求我们找规律，于是我就在草稿纸上画了很多个图像，还是没有找到规律，于是我就在网上看了些大佬 的代码，发现他们用了欧拉公式，what 什么是欧拉公式，~~~~~~~~~~~~~~~~~

Google了哈，看了哈百度百科的解释，一下是我看懂的部分，看上去很高大上，实际很实用。

欧拉公式

在任何一个规则球面地图上，用 R记区域个 数 ，V记顶点个数 ，E记边界个数 ，则 R+ V- E= 2，这就是欧拉公式。

 区域+顶点-边界=2

柯西的证明

第一个欧拉公式的严格证明，由20岁的柯西给出，大致如下：

 

 

从多面体去掉一面，通过把去掉的面的边互相拉远，把所有剩下的面变成点和曲线的平面网络。不失一般性，可以假设变形的边继续保持为直线段。正常的面不再是正常的多边形即使开始的时候它们是正常的。但是，点，边和面的个数保持不变，和给定多面体的一样(移去的面对应网络的外部。)

重复一系列可以简化网络却不改变其欧拉数（也是欧拉示性数）

  

的额外变换

若有一个多边形面有3条边以上，我们划一个对角线。这增加一条边和一个面。继续增加边直到所有面都是三角形。

1. 除掉只有一条边和外部相邻的三角形。这把边和面的个数各减一而保持顶点数不变。
2. （逐个）除去所有和网络外部共享两条边的三角形。这会减少一个顶点、两条边和一个面。

重复使用第1步和第2步直到只剩一个三角形。对于一个三角形

  

（把外部数在内）

  

，

  

。所以

  

。

//在每次进行1 2步骤时，都是符合公式 。//

推理证明

设想这个多面体是先有一个面，然后将其他各面一个接一个地添装上去的.因为一共有F个面，因此要添(F-1)个面.

考察第Ⅰ个面，设它是n边形，有n个顶点，n条边，这时E=V，即棱数等于顶点数.

添上第Ⅱ个面后，因为一条棱与原来的棱重合，而且有两个顶点和第Ⅰ个面的两个顶点重合，所以增加的棱数比增加的顶点数多1，因此，这时E=V+1.

以后每增添一个面，总是增加的棱数比增加的顶点数多1，例如

增添两个面后，有关系E=V+2;

增添三个面后，有关系E=V+3;

……

增添(F-2)个面后，有关系E=V+ (F-2).

最后增添一个面后，就成为多面体，这时棱数和顶点数都没有增加.因此，关系式仍为E=V+ (F-2).即

F+V=E+2.

这个公式叫做欧拉公式.它表明2这个数是简单多面体表面在连续变形下不变的数。

Code：

但是要注意的是，当区域只有一个时，表明这些顶点没有相连，又要满足没有都至少有两个曲线的要求，要单独算，例如n=4,n=1，如图

#include <cstdio>
#include <algorithm>

int main()
{
    long long n,m;
    while(scanf("%lld%lld",&n,&m),n+m)
    {
        if(m==1)
        {
            printf("%lld
",n+1);
        }
        else
        {
            printf("%lld
",n+m-2);
        }
    }
    return 0;
}

 实际上 ，觉得题目有问题，当n=6 ,m=3时 欧拉公式就是7，我还可能画出6.

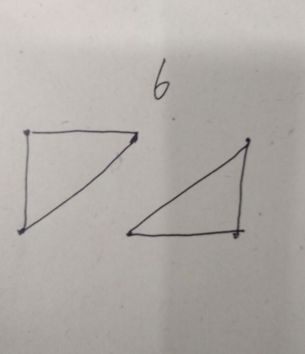
后来，我觉得，题目应该多个要求，那就是：一个个图形不能用多个图形来划分区域。