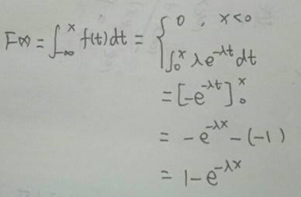2、 一维随机变量的分布
(1)随机变量
类型-----根据取值情况的不同可以将随机变量分为离散随机变量和连续随机变量
概率分布-----随机变量一切可能值或范围的概率的规律
(2)常见离散分布
1)两点分布
随机变量X值可能取0和1两个值,则分布为
|
X |
0 |
1 |
|
Pk |
1-P |
P |
则称X服从(0--1)分布或者两点分布
2)二项分布
在一次试验E中只考虑两个互逆的结果A或者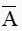 ,这样的试验称为伯努利试验。
,这样的试验称为伯努利试验。
n重伯努利试验:将伯努利试验E独立(表示每次试验的结果都互不影响)的重复(表示在这n次试验中P(A)=p保持不变)进行n次,那么这一连串重复的独立试验就是n重伯努利试验。

3)泊松分布
设随机变量所有可能取值为0,1,2,……,而取每个值得概率为![]() ,其中
,其中![]() 是常数,则称X服从参数为
是常数,则称X服从参数为![]() 的泊松分布,记为X~Pois(
的泊松分布,记为X~Pois(![]() )
)
4)二项分布于泊松分布的关系


(3)连续随机变量
由于对连续随机变量X有P(X=x)= 0,所以无法效仿离散随机变量用P(X=x)来描述连续随机变量X的分布,而是通过给出所谓的概率密度函数(简称概率密度)的方式。

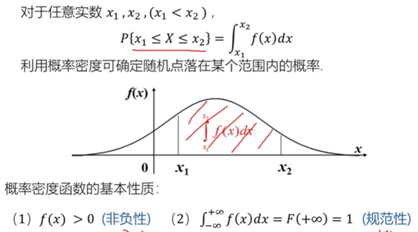
(4)常见连续分布
1)正态分布

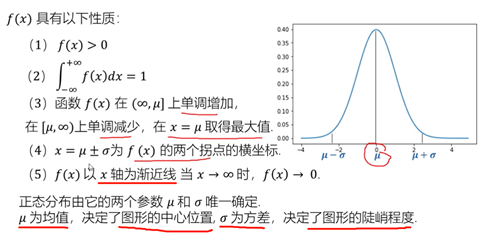
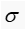 越大,x的取值就会越分散,曲线就越平缓;
越大,x的取值就会越分散,曲线就越平缓;
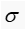 越小,x的取值就比较集中,曲线就比较陡峭。
越小,x的取值就比较集中,曲线就比较陡峭。
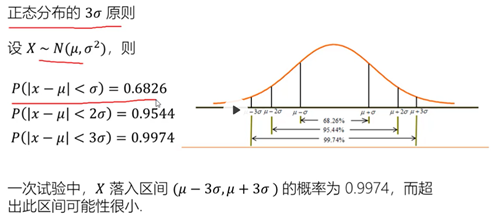
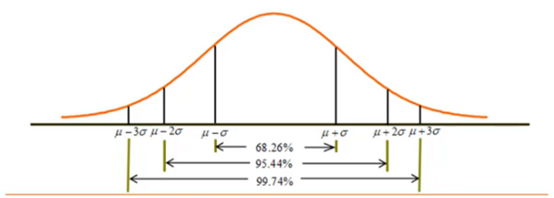
2)标准正态分布
标准正态分布是![]() 的正态分布,即X~N(0,1)
的正态分布,即X~N(0,1)
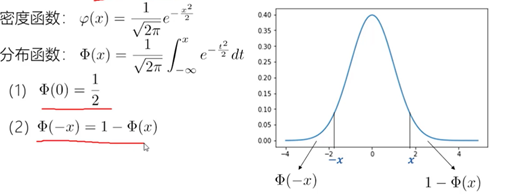
一般正态分布的标准化
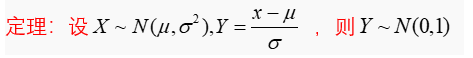

标准正态分布的重要性在于,任何一个一般的正态分布都可以通过线性变换转化成标准正态分布。

3)均匀分布

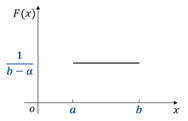

4)指数分布