基本思想:将一组要排序的数列分成两部分,其中一部分的值都比另一部分的小;然后按照这个方法分别对两部分数据进行快速排序,整个过程可以用递归进行,从而实现整个数列的排序。
快速排序方法是基于分值策略的,排序在原地排序,不需要辅助的数组,但是分解困难。
快速排序分为三个过程:分解、治理、合并。
分解:先从数列num[low,high]中取出一个基准元素,将所有比基准元素小的数据存放在基准元素左侧,将所有比基准元素大的数据存放在基准元素右侧;基准元素此时已经位于正确的位置了,这个位置记为mid;
治理:基准元素左右两个子数列num[low,mid-1]和num[mid+1,high]进行分解的操作,即进行快速排序的操作,这一步通过递归的方式实现;
合并:由于快速排序是在原地进行排序,因此不需要进行合并的操作。
快速排序中一个注意点的是基准元素该如何选择?如果基准元素选取不当,有可能分解成规模为0和n-1的两个子数列,快速排序会退化成冒泡排序。
一般来说,基准元素有以下几种取法:
- 取第一个元素
- 取最后一个元素
- 取中间元素
- 取第一个、最后一个、中间位置元素三者的中位数
- 取第一个和最后一个之间位置的随机数k(low<=k<=high),取R[k]作为基准元素
快速排序的算法中,第二步是递归,关键的第一步分解如何实现呢?也就是说,我们选择好了基准元素后,如何将数列中比基准元素小的数都移到基准元素左边,而把数列中比基准元素大的数都移动到基准元素右边呢?
下面选择基准元素为第一个元素,说明如何实现这一步。
假设当前待排序的数列为num[low,high],其中low<=high。
步骤1:首先取数组的第一个元素作为基准元素pivot = num[low], 设置两个指针i和j,i = low, j = high;
步骤2:从右向左扫描(即 j不断向左移动),找到小于 pivot 的数,如果找到的话,num[i] 和 num[j] 交换, i++;(这一步其实就是将比基准元素小的数移动到基准元素左边)
步骤3:从左向右扫描(即 i 不断向右移动),找到大于 pivot 的数,如果找到的话,num[i] 和 num[j] 交换,j--;(这一步其实就是将比基准元素大的数移动到基准元素左右边)
步骤4:重复步骤2~步骤3,直到指针 i 和 j 重合,返回该位置 mid = i,该位置的数正好是pivot
以数组{30,24,5,58,18,36,12,42,39}为例,上述步骤的演示过程如图

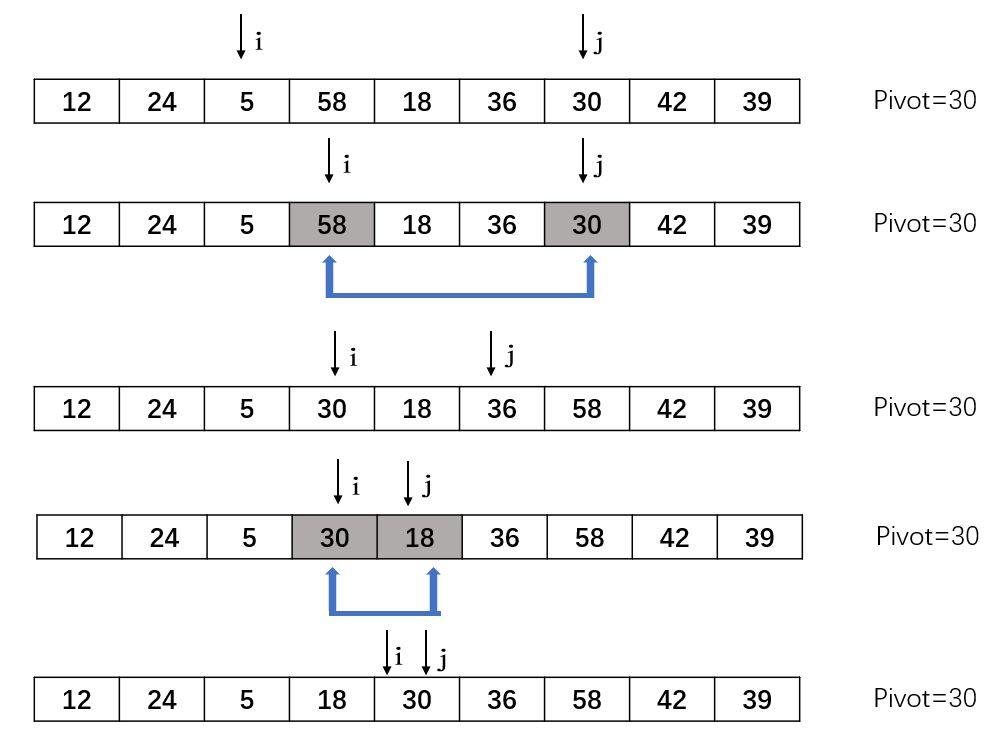
实现代码如下所示:
1 public static void main(String[] args){ 2 int[] num = {30,24,5,58,18,36,12,42,39}; 3 QuickSort(num,0,num.length-1); 4 for(int k:num) 5 System.out.print(k+","); 6 } 7 public static void QuickSort(int[] num,int low,int high) { 8 int mid; 9 if(low<high) { 10 mid = Partition(num,low,high); 11 QuickSort(num,low,mid-1); 12 QuickSort(num,mid+1,high); 13 } 14 } 15 public static int Partition(int[] num, int low, int high) { 16 int i = low; 17 int j = high; 18 int pivot = num[low]; 19 while(i < j) { 20 while(i < j && num[j] > pivot) 21 j--; 22 if(i<j) { 23 swap(num,i,j); 24 i++;//注意,这一行不能在花括号外面 25 } 26 while(i<j && num[i]<pivot) 27 i++; 28 if(i<j) { 29 swap(num,i,j); 30 j--;//注意,这一行不能在花括号外面 31 } 32 } 33 return i; 34 } 35 public static void swap(int[] num,int i,int j) { 36 int tmp = num[j]; 37 num[j] = num[i]; 38 num[i] = tmp; 39 }
需要注意的是,以上Partition()函数的实现只适用于基准元素是第一个元素的时候,当基准元素取最后一个元素时,需要将步骤2和步骤3调换。我们仔细看上述过程,会发现,指针i和j总有一个是指向基准元素,在做交换过程的时候,是基准元素和其它元素在做交换。如果我们将基准元素取最后一个元素是,可能会发生指针i和j指向的不是基准元素了。
在代码中,我有两行加了注释,就是指针i++和指针j--这一过程必须在花括号里。这是因为只有在i<j的情况下,才能执行 i++和j--的操作。否则的话,当i==j了,此时需要换回i,如果i++不在i<j的约束下,肯定是要执行的,返回的就不是基准元素的位置,而是基准元素后一位了。