Codeforces Round #394 (Div. 2) B. Dasha and friends —— 暴力 or 最小表示法

题目链接：http://codeforces.com/contest/761/problem/B

B. Dasha and friends

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Running with barriers on the circle track is very popular in the country where Dasha lives, so no wonder that on her way to classes she saw the following situation:

The track is the circle with length L, in distinct points of which there are n barriers. Athlete always run the track in counterclockwise direction if you look on him from above. All barriers are located at integer distance from each other along the track.

Her friends the parrot Kefa and the leopard Sasha participated in competitions and each of them ran one lap. Each of the friends started from some integral point on the track. Both friends wrote the distance from their start along the track to each of the n barriers. Thus, each of them wrote n integers in the ascending order, each of them was between 0 and L - 1, inclusively.

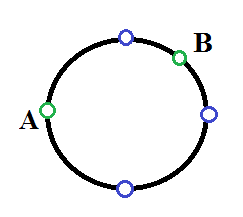
Consider an example. Let L = 8, blue points are barriers, and green points are Kefa's start (A) and Sasha's start (B). Then Kefa writes down the sequence[2, 4, 6], and Sasha writes down [1, 5, 7].

There are several tracks in the country, all of them have same length and same number of barriers, but the positions of the barriers can differ among different tracks. Now Dasha is interested if it is possible that Kefa and Sasha ran the same track or they participated on different tracks.

Write the program which will check that Kefa's and Sasha's tracks coincide (it means that one can be obtained from the other by changing the start position). Note that they always run the track in one direction — counterclockwise, if you look on a track from above.

Input

The first line contains two integers n and L (1 ≤ n ≤ 50, n ≤ L ≤ 100) — the number of barriers on a track and its length.

The second line contains n distinct integers in the ascending order — the distance from Kefa's start to each barrier in the order of its appearance. All integers are in the range from 0 to L - 1 inclusively.

The second line contains n distinct integers in the ascending order — the distance from Sasha's start to each barrier in the order of its overcoming. All integers are in the range from 0 to L - 1 inclusively.

Output

Print "YES" (without quotes), if Kefa and Sasha ran the coinciding tracks (it means that the position of all barriers coincides, if they start running from the same points on the track). Otherwise print "NO" (without quotes).

Examples

input

3 8
2 4 6
1 5 7

output

YES

input

4 9
2 3 5 8
0 1 3 6

output

YES

input

2 4
1 3
1 2

output

NO

Note

The first test is analyzed in the statement.

题解：

n的范围为：1~50， 所以即使O（n^3）的复杂度仍绰绰有余。

两个环相等的充要条件：这两个环上的每相邻两点间隔对应相等（大小及次序）。

有关下标循环的小细节：

1.当下标的范围为：0~n-1， 则 i = (i+step)%n;

2.当下标的范围为：1~n，    则 i = (i+step<=n)? (i+step) : (i+step)%n。当step=1时， 可简写为：i = (i%n)+1。

暴力 O（n^2）:

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const double eps = 1e-6;
const int INF = 2e9;
const LL LNF = 9e18;
const int mod = 1e9+7;
const int maxn = 100+10;

int n,L;
int a[maxn], b[maxn];   //下标从1开始

int main()
{
    cin>>n>>L;
    for(int i = 1; i<=n; i++)
        cin>>a[i];
    for(int i = 1; i<=n; i++)
        cin>>b[i];

    a[n+1] = L+a[1], b[n+1] = L+b[1];   //因为环，所以要求出尾到首的距离
    for(int i = 1; i<=n; i++)
    {
        a[i] = a[i+1]-a[i];   //求出甲的间隔距离
        b[i] = b[i+1]-b[i];   //求出乙的间隔距离
    }

    int B = 0;
    for(int k = 0; k<n; k++) //错开的幅度
    {
        int i;
        for(i = 1; i<=n; i++)   //甲间隔的下标
        {
            int j = (i+k)<=n?(i+k):(i+k)%n;    //乙间隔的下标，因为循环，所以要特判。
            if(a[i]!=b[j])
                break;
        }
        if(i==1+n)  //间隔距离完全匹配
        {
            B = 1;
            break;
        }
    }

    printf("%s
",B?"YES":"NO");
}

最小表示法 O（n）:

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const double eps = 1e-6;
const int INF = 2e9;
const LL LNF = 9e18;
const int mod = 1e9+7;
const int maxn = 100+10;

int n,L;
int a[maxn], b[maxn];   //下标从0开始

int getmin(int *s, int len) //返回最小表示法的始端
{
    int i = 0, j = 1, k = 0;
    while(i<len && j<len && k<len)
    {
        int t = s[(i+k)%len]-s[(j+k)%len];
        if (!t) k++;
        else
        {
            if (t>0) i += k+1;
            else j += k+1;
            if (i==j) j++;
            k = 0;
        }
    }
    return i<j?i:j;
}

int main()
{
    cin>>n>>L;
    for(int i = 0; i<n; i++)
        cin>>a[i];
    for(int i = 0; i<n; i++)
        cin>>b[i];

    a[n] = L+a[0], b[n] = L+b[0];   //因为环，所以要求出尾到首的距离
    for(int i = 0; i<n; i++)
    {
        a[i] = a[i+1]-a[i];   //求出甲的间隔距离
        b[i] = b[i+1]-b[i];   //求出乙的间隔距离
    }

    int B = 1;
    int t1 = getmin(a, n);
    int t2 = getmin(b, n);
    for(int i = 0; i<n; i++)
    {
        int k1 = (t1+i)%n;
        int k2 = (t2+i)%n;
        if(a[k1]!=b[k2])
        {
            B = 0;
            break;
        }
    }

    printf("%s
",B?"YES":"NO");
}