主要内容:
一.关联分析
二.Apriori原理
三.使用Apriori算法生成频繁项集
四.从频繁项集中生成关联规则
一.关联分析
1.关联分析是一种在大规模数据集中寻找有趣关系的任务。这些关系可以有两种形式:频繁项集和关联规则。
2.频繁项集是经常出现在一起的元素的集合。
3.关联规则暗示两个元素集合之间可能存在很强的关系。形式为:A——>B,就是“如果A,则B”。
4.支持度:数据集中包含该项集的数据所占的比例,支持度高的项集就为频繁项集。
5.可信度(置信度):衡量关联规则可信程度的标准,假设A出现的概率为P(A),AB出现的概率为P(AB),则可信度为P(B|A) = P(AB)/ P(A)。
二.Apriori原理
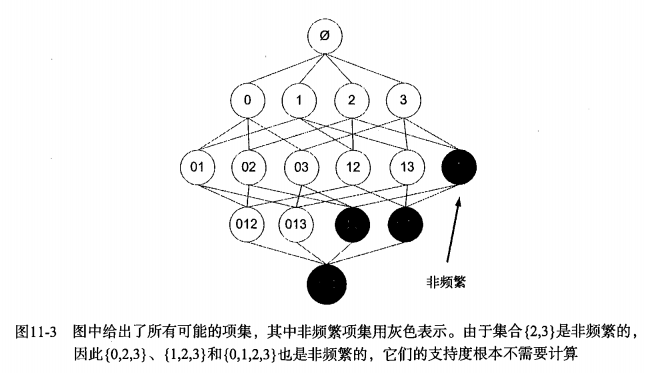
1.Apriori原理是说如果某个项集是频繁的,那么它的所有子集也是频繁的。p --> q ==> !q --> !p ,所以:如果一个项集是非频繁项集,那么它的所有超集也是非频繁项集。
2.Apriori原理可以帮我们去除掉很多非频繁项集。因为我们可以在项集规模还是很小的时候,假如能确定他是非频繁的,那么就可以直接去除掉那些含有该项集的更大的项集了,从而减少了运算的规模。
3.例子如下:

三.使用Apriori算法生成频繁项集
1.算法步骤:
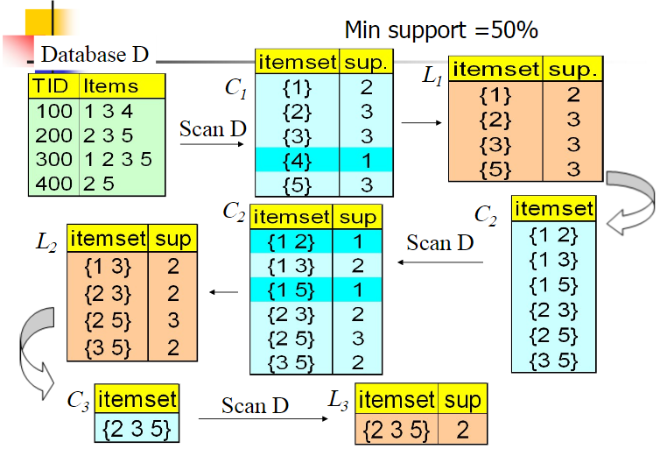
1)根据数据集,生成单位项集C1,然后计算项集C1的支持度,并从中挑选出频繁项集构成L1(频繁项集的划分边界为一个阈值 Mini support)。
2)设已经完成的最新一层的频繁项集的项数为k,而这一层可称为第k层,可知k初始化为1。判断这一层频繁项集的个数是否大于1:如果大于1,则表明至少存在两个频繁项集可以两两合并成一个新的项集Ck+1,然后计算其支持度并过滤出频繁项集,生成第k+1层。
3)重复执行第2)步,直到最新一层的频繁项集的个数少于等于1。
注:两个频繁项集合并时,需要限定:两者有k-1个元素是相同的,然后两者合并之后,就形成了一个k+1的集合。假如两个频繁项集的相同元素少于k-1个,那他们合并后的新项集的项数必定大于k+1,对于此种情况就直接忽略掉,让它在往后的那些层再重新被考虑。这样就能够保证每一层的频繁项集的项数是相同的。
2算法流程图:
3.Python代码:
1 def createC1(dataSet): #生成单位项集 2 C1 = [] 3 for transaction in dataSet: #枚举每一条数据 4 for item in transaction: #枚举每条数据中的每个元素 5 if not [item] in C1: 6 C1.append([item]) #将素有元素加入列表中 7 C1.sort() #必要的排序 8 return map(frozenset, C1) # use frozen set so we can use it as a key in a dict 9 10 def scanD(D, Ck, minSupport): #计算项集的支持度,并过滤掉支持度低于阈值的项集,从而形成频繁项集。Ck的k代表项集的项数 11 ssCnt = {} 12 for tid in D: #统计项集在数据中的出现次数 13 for can in Ck: 14 if can.issubset(tid): 15 if not ssCnt.has_key(can): 16 ssCnt[can] = 1 17 else: 18 ssCnt[can] += 1 19 numItems = float(len(D)) 20 retList = [] #频繁项集列表 21 supportData = {} #保存项集的支持度,是一个字典。注意:非频繁项集也保存。 22 for key in ssCnt: 23 support = ssCnt[key] / numItems #支持度 24 if support >= minSupport: 25 retList.insert(0, key) #频繁项集 26 supportData[key] = support #保存支持度 27 return retList, supportData 28 29 def aprioriGen(Lk, k): # 用于生成下一层的频繁项集(即项数是当前一次的项数+1狼,即k) 30 retList = [] 31 lenLk = len(Lk) 32 for i in range(lenLk): #O(n^2)组合生成新项集 33 for j in range(i + 1, lenLk): 34 L1 = list(Lk[i])[:k - 2]; L2 = list(Lk[j])[:k - 2] #去除两者的前k-2个项 35 L1.sort(); L2.sort() 36 if L1 == L2: # 如果前k-2个项相等,那么将Lk[i]和Lk[j]并在一起,就形成了k+1个项的项集 37 retList.append(Lk[i] | Lk[j]) # set union 38 return retList 39 40 def apriori(dataSet, minSupport=0.5): #Apriori算法 41 D = map(set, dataSet) #set形式数据集(即去除重复的数据) 42 C1 = createC1(dataSet) #单位项集 43 L1, supportData = scanD(D, C1, minSupport) #单位频繁项集 44 L = [L1] 45 k = 2 46 while (len(L[k - 2]) > 1): #如果当层的频繁项集的个数大于1,那么就可以根据当层的频繁项集生成下一层的频繁项集 47 Ck = aprioriGen(L[k - 2], k) #生成下一层的项集 48 Lk, supK = scanD(D, Ck, minSupport) # 生成下一层的频繁项集,同时得到项集的支持度 49 supportData.update(supK) #更新支持度库 50 L.append(Lk) #把下一层的频繁项集加入到“层叠”里面 51 k += 1 #将下一层作为当层 52 return L, supportData
四.从频繁项集中生成关联规则
1.为何要从频繁项集中生成关联规则?因为频繁项集意味着出现的频率更高,从中得到的规则更能让人信服(这里不是指可信度)。举个反例,如果A和B只出现过一次,且两者一起出现即AB,我们就可以得到结论A-->B的可信度为100%,但AB的出现可能就是一个噪音,贸贸然下定论并非合理。所以要从频繁项集中生成关联规则。
2.如何从频繁项集中生成关联规则?简而言之就是挑选一个频繁项集,如{ABCD},首先把它作为规则的前件,然后逐渐把元素往后件移,如A-->BCD、B-->ACD、C-->ABD、D-->ABC、AB-->CD……等等。但具体又如何操作呢?难道要用数学中组合的方式?这样计算量太大了。这里有个事实:如果某条规则并不满足最小可信度要求,那么该规则的所有子集也不会满足最小可信度要求。如下:
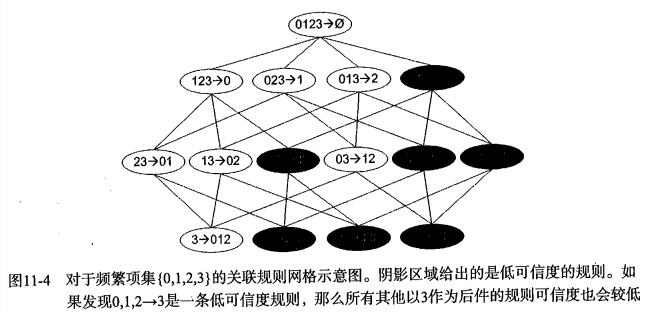
可知{0,1,2}-->{3}的可信度为 P({3})/ P({0,1,2}),如果{0,1,2}-->{3}是低可信度规则,那么{0,1}-->{2,3} 、{2}-->{0,1,3}等等3在后件的那些规则,统统都为低可信度规则。原因就在于可信度的计算公式:对于{0,1,2}-->{3},其可信度为P({3})/ P({0,1,2}),此时如果把0从前件移到后件,那么就成了{1,2}-->{0,3},其可信度为P({0,3})/ P({1,2}),较之于P({3})/ P({0,1,2}),其分子减小了,其分母增大了,所以P({0,3})/ P({1,2})< P({3})/ P({0,1,2})。所以:如果{0,1,2}-->{3}是低可信度规则,那么{1,2}-->{0,3}也是低可信度规则。
简而言之:对于在同一个频繁项集内形成的关联规则,假如某规则为低可信度规则,那么规则后件是该低可信度规则后件的超集的规则,都是低可信度规则。因此可以直接去掉。
3.算法流程:
1)枚举每一层的每一个频繁项集,将其作为生成关联规则的当前项集freSet,同时将freSet的单个元素作为单位项集以作为关联规则后件H。
2)如果关联规则后件的项数小于当前项集freSet的项数,则前件后件都不为空,此时:枚举关联后件H,将freSet-H作为前件,将H作为后件,然后计算其可信度,并筛选出可信度高的关联规则,同时筛选出能生成高可信度规则的后件H(大大简化计算量)。
3)如果筛选过后的后件H的个数大于1,则表明可以生成当前后件项数+1的后件,那么就调用Apriori算法生成新一层的后件Hnext,将Hnext作为H,然后重复第2)步。
4.Python代码:
1 def calcConf(freqSet, H, supportData, brl, minConf=0.7): #计算关联规则的可信度,关联规则的右端的元素个数是固定的 2 prunedH = [] # create new list to return 3 for conseq in H: #conseq作为关联规则的右端 4 conf = supportData[freqSet] / supportData[freqSet - conseq] # 计算可信度 5 if conf >= minConf: #可信度大于等于阈值,则将关联规则存储起来 6 print freqSet - conseq, '-->', conseq, 'conf:', conf 7 brl.append((freqSet - conseq, conseq, conf)) #将关联规则存储起来 8 prunedH.append(conseq) #将能生成关联规则的频繁项集存起来 9 return prunedH 10 11 def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7): 12 m = len(H[0]) #关联规则的右端的元素个数 13 if (len(freqSet) > m): #如果总的元素个数大于关联规则的右端的元素个数,则继续生成关联规则 14 Hitem = calcConf(freqSet, H, supportData, brl, minConf) #生成关联规则, 同时过滤出有用的频发项集 15 if (len(Hitem) > 1): # 频繁项集的个数超过一个,则可以生成下一层的项集(即关联规则的元素个数右端加一,对应地左端减一) 16 Hnext = aprioriGen(Hitem, m + 1) # create Hm+1 new candidates 17 rulesFromConseq(freqSet, Hnext, supportData, brl, minConf) 18 19 def generateRules(L, supportData, minConf=0.7): # 生成关联规则 20 bigRuleList = [] #关联规则列表 21 for i in range(1, len(L)): # 枚举每一层(也可以说枚举长度,从第二层开始,因为关联最少要有两个元素) 22 for freqSet in L[i]: #枚举这一层中所有的频繁项集,用于生成关联规则 23 H1 = [frozenset([item]) for item in freqSet] #将频繁项集中的元素单独作为一个集合,然后这些集合构成一个列表 24 rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf) #递归地将freqSet中的元素移到关联规则的右端,从而生成关联规则 25 return bigRuleList