问题 A: 组合数

问题 A: 组合数

时间限制: 1 Sec  内存限制: 128 MB
提交: 1975  解决: 150
[提交] [状态] [命题人:jsu_admin]

题目描述

求组合数C(N,M)，以及C(N,M)因子个数。

输入

N和M，其中0<=M<=N<=50,以EOF结束。

输出

该组合数结果

样例输入 Copy

3 2
4 2

样例输出 Copy

3 2
6 4

因为求组合数的时候 long long 存不下，所以我们需要分解质因数再求解，它的就是把分子分母约去同时有的素因子以达到中间算阶乘的时候不会爆 long long

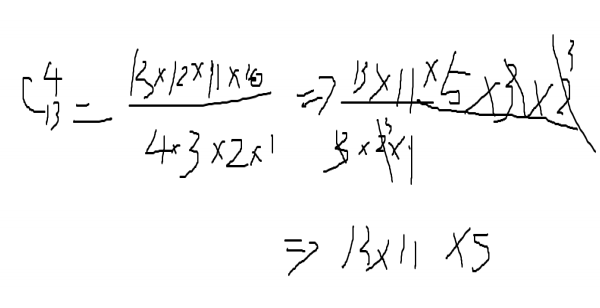
计算因子数用到了唯一分解定理
一个数 n 肯定能被分解成 n=p1^r1 * p2^r2 . . .*pn^rn
假设 p1p2,…pn 是它的素因子
假设 r1,r2,…rn 分别是 p1…pn 的幂次数
那么（1+r1）*（1+r2）….*(1+rn)就是他的因子数

/**
/*两个板子 快速幂+组合数
*/
#include<stdio.h>
#include <iostream>
#include <bits/stdc++.h>
#define maxn 200005
typedef long long ll;
using namespace std;
const ll mod=998244353;
ll fac[maxn],inv[maxn];
ll pow_mod(ll a,ll n)
{
    ll ret =1;
    while(n)
    {
        if(n&1) ret=ret*a%mod;
          a=a*a%mod;
          n>>=1;
    }
    return ret;
}
void init()
{
    fac[0]=1;
    for(int i=1;i<maxn;i++)
    {
        fac[i]=fac[i-1]*i%mod;
    }
}
ll Cc(ll x, ll y)
{
    return fac[x]*pow_mod(fac[y]*fac[x-y]%mod,mod-2)%mod;
}
//ll pow(ll x,ll n)
//{
//ll temp(x),res(1);
//while(n)
//{
//if(n&1) 
//{
//res *= temp;
//}
//temp *= temp;
//n>>=1;
//}
//return res;
//}

long long C[1000][1000];
ll D(ll m,ll n)
{
    for(int i=1;i<50;++i)
    {
        C[i][i]=1;
        C[i][0]=1;
    }
    for(int i=1;i<50;++i)
    {
        for(int j=i+1;j<50;++j)
        {
            C[j][i]=C[j-1][i-1]+C[j-1][i];
        }
    }
   // int m,n;
//    while(cin>>m>>n)///C(m,n)
//    {
//        cout<<C[m][n]<<endl;
//    }
    return C[m][n];
}
#define N 440
int prime[N];
bool vis[N];
double fact(int n)//求阶乘
{
int i;
double sum;
sum=1;
for(i=1;i<=n;i++)
{
sum=sum*i;
}
return sum;
} 


int Prime()
{
    int cnt = 0;
    for (int i = 2; i <= N; ++i)
    {
        if (!vis[i])
        {
            prime[cnt++] = i;
        }
        for (int j = 0; j < cnt&&i*prime[j] <= N; ++j)
        {
            vis[i*prime[j]] = 1;
            if (i%prime[j] == 0)break;
        }
    }
    return cnt;
}
int num[500];
int Fcnt;
void solve(int n,int y)
{
    for (int i = 0; i < Fcnt; ++i)
    {
        int c = 0, p = prime[i];
        while (n / p )
        {
            c += n / p;
            p *= prime[i];
        }
        num[i] = num[i] + y*c;
    }
}

//int main()
//{
//    Fcnt=Prime();
//    int n, m;
//    while (scanf("%d%d", &n, &m) != EOF){
//        memset(num, 0, sizeof(num));
//        solve(n, 1);
//        solve(m, -1);
//        solve(n - m, -1);
//        ll ans = 1;
//        for (int i = 0; i < Fcnt; ++i)
//        {
//            ans *= (num[i] + 1);
//        }
//        printf("%lld
", ans);
//    }
//}
int main(){
    ll p,q,k,a,b;
        Fcnt=Prime();
int n,m;
double n1,m1,o1;
double fact(int n);
    while(scanf("%lld%lld%lld%lld%lld",&p,&q,&n,&m,&b)!=EOF){
            printf("%lld
",p);
    n1=fact(n);
m1=fact(m);
o1=fact(n-m);
int k = 0;
 memset(num, 0, sizeof(num));
        solve(n, 1);
        solve(m, -1);
        solve(n - m, -1);
        ll ans = 1;
for(int i = 1;i*i<=((int)(n1/(m1*o1)));i++){
    if((int)(n1/(m1*o1))%i==0)
    k++;
} 
printf("%.0f ",n1/(m1*o1),k);

//    ll CC = (long long)D(k,a); 
    ll aa = (long long)pow(q,m);
    ll bb = (long long)pow(p,b);
    ll sum = ((long long)(n1/(m1*o1)))*aa*bb;
//    printf("%lld
",CC);
    printf("%lld
",p);
    printf("%lld
",sum);
}
}