联考20200526 T1 a

分析：
当(K=1)时就随便做了，我们考虑(K=2)的情况
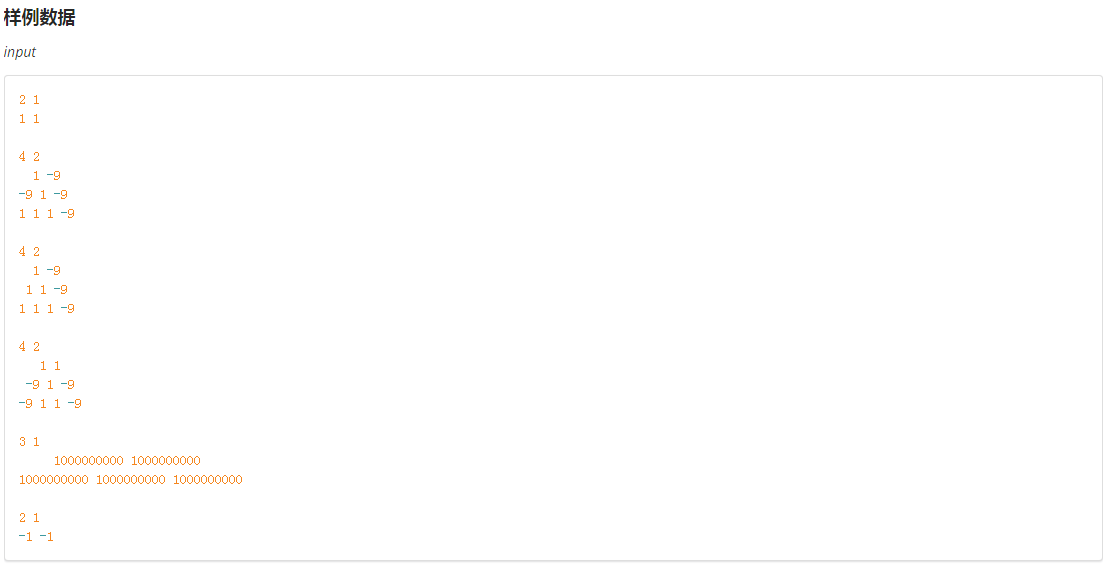
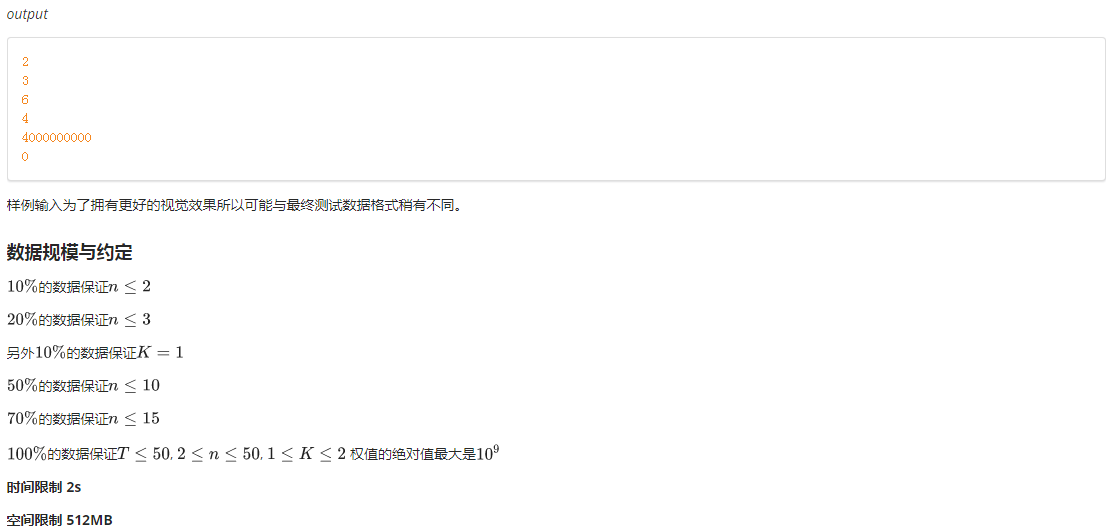
我们来大致观察一下整个过程

蓝色为第一天，红色为第二天
我们转一下整个图，把等腰直角三角形补全为正方形，补出来的点值设为0，对答案显然不会影响

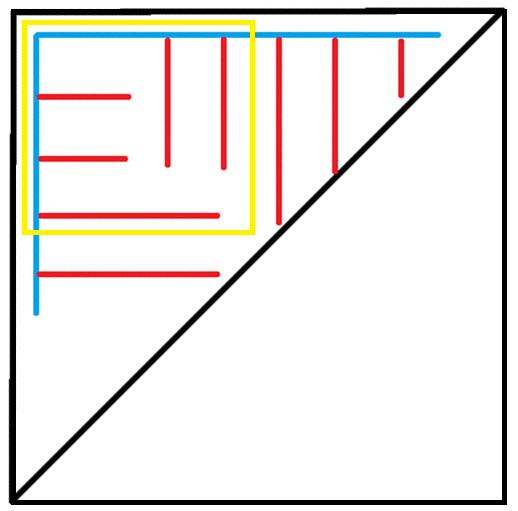
我们观察黄色部分，这部分的一些红线被另一个方向的红线阻挡了去路
考虑一下这种矩形最大的贡献
设(f[i][j])表示右下角为((i,j))的矩形的最大贡献

(f[i][j]=max(f[i-1][j]+mxr[i][j],f[i][j-1]+mxc[i][j]))

分别表示((i,j))这个点朝上还是朝左的贡献，(mxr)和(mxc)分别表示该点向左向上一条直线上的前缀最大贡献
相交的部分搞定了以后，不相交的部分就一路挖到底，找前缀最大值就好了

#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<queue>
#include<algorithm>

#define maxn 55
#define INF 0x3f3f3f3f

using namespace std;

inline int getint()
{
	int num=0,flag=1;char c;
	while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
	while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
	return num*flag;
}

int n,K;
long long a[maxn][maxn],f[maxn][maxn];
long long suma[maxn][maxn],sumb[maxn][maxn];
long long mxa[maxn][maxn],mxb[maxn][maxn];
long long summxa[maxn],summxb[maxn];
long long ans;

int main()
{
	int T=getint();
	while(T--)
	{
		n=getint();K=getint();ans=0;
		memset(a,0,sizeof a);memset(f,0,sizeof f);
		memset(suma,0,sizeof suma);memset(mxa,-INF,sizeof mxa);
		memset(sumb,0,sizeof sumb);memset(mxb,-INF,sizeof mxb);
		for(int i=2;i<=n;i++)for(int j=1;j<=i;j++)
			a[i-j+1][j]=getint();
		for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)
		{
			suma[i][j]=suma[i][j-1]+a[i][j];
			sumb[j][i]=sumb[j][i-1]+a[i][j];
			mxa[i][j]=max(mxa[i][j-1],suma[i][j]);
			mxb[j][i]=max(mxb[j][i-1],sumb[j][i]);
		}
		if(K==1){printf("%lld
",mxa[1][n]+mxb[1][n]);continue;}
		for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)
		{
			if(i==1)f[i][j]=suma[1][j];
			else if(j==1)f[i][j]=sumb[1][i];
			else f[i][j]=max(f[i-1][j]+mxa[i][j],f[i][j-1]+mxb[j][i]);
		}
		for(int i=1;i<=n;i++)
		{
			long long s=f[i][1],t=0;
			for(int j=1;j<=n;j++)s=max(s,f[i][j]);
			for(int j=i+1;j<=n;j++)t+=mxa[j][n],ans=max(ans,s+t);
		}
		for(int i=1;i<=n;i++)
		{
			long long s=-1ll<<60,t=0;
			for(int j=1;j<=n;j++)s=max(s,f[j][i]);
			for(int j=i+1;j<=n;j++)t+=mxb[j][n],ans=max(ans,s+t);
		}
		printf("%lld
",ans);
	}
}