梯度下降算法
-
梯度
- 函数上某一点的梯度是 向量,就是函数变化增加最快的地方。具体来说,对于函数f(x,y),在点(x0,y0)沿着梯度向量的方向 : (df/dx0,df/dy0)的转置. 可以最快速度到达最大值.
-
梯度下降算法
-
损失函数: J(w)
-
w的梯度将是损失函数上升最快的方向,最小化loss ,反向即可 J(w_old) ---->J(w_old- k * ▽w_old的梯度)---->J(w_new)
-
方法 : 主要区别是每一次更新样本参数使用的样本个数是不同的
-
批量梯度下降
-
使用全部数据进行参数更新
-
w = w-k * ▽J(w)
-
for i in range(nb_epochs): params_grad = evaluate_gradient(loss_function,data,params) params = params - learning_rate * pramas_grad -
每次更新梯度使用全部数据 ,最后梯度可为0
-
-
随机梯度下降
-
w = w - k * ▽ J(w;xi;yi)
-
使用一个样本更新模型,速度快
-
for i in range(nb_epochs): np.random.shuffle(data) for example in data: params_grad = evalute_gradient(loss_function,example,params) params = params - leaning_rate * params_grad -
学习率需要逐渐减少,否则无法收敛
-
-
小批量梯度下降
-
w = w - k * ▽J(w;xi:i+m;yi:i+m) 每次更新从训练集选取m个样本学习 m小于总体个数
-
for i in range(pb_epochs): np.random.shuffle(data) for batch in get_batch(data,batch_size=50): params_grad = evalute_gradient(loss_function,batch,params) params = params - leaning_rate * params_grad
-
-
-
-
问题
- 合适的学习率很难找
- 跟新每次的学习率方式很难,需要设置阈值,跟新学习率,不能自适应数据集的特点
- 模型搜友的参数每次跟新都是使用相同的学习率, 对于稀疏数据等效果不好
- 对于非凸函数,容易陷入次忧的局部极值中
-
优化梯度下降
-
SGD
-
Momentum
-
基于动量的算法
-
前几次的梯度会参与到本次梯度的计算
-
原来:w = w - learning_rate * dw
-
现在:
v = alpha * v - learning_rate *dw
w = w+v
-
v 是初始速度,alpha是指数衰减系数,也叫作动量参数 常见设置为0.9
-
理解为 上次梯度与这次相同,那么下次下降速度幅度会加大,从而加速收敛
-
-
-
Nesterov Momentum
-
先对参数进行估计,然后使用估计后的参数来计算误差
-
学习率ε 初始参数 θ 初始速率v 栋梁衰减参数 α
-
过程:
-
从训练集中随机抽取m个样本,及他们的标签
-
计算梯度和误差 ,跟新速度v和参数α
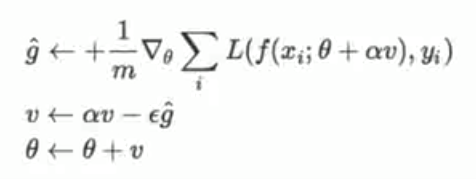
-
-
-
AdaGrad
- 自适应为各个参数分配不同的学习率
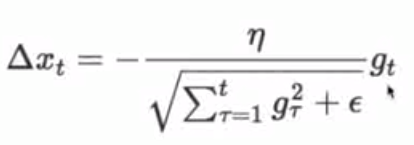
- 需要全局学习率
- Adadelta

-
RMSProp
-
Adam
-
-
学习率的设定

学习率的设定
global_step = tf.Variable(0,trainble=False) starter_learning = 0.1 # 初始学习率为0.1 # 每隔10000次学习率变为原来的0.96 learning_rate = tf.exponential_dacay(starter_learning_rate, global_setp,10000,0.96,staircase=True) optimizer = tf.GradientDescent(learning_rate) optimizer.minimize(...my_loss...,global_step=global_setp)