bitmap和布隆过滤器
海量整数中是否存在某个值--bitmap
在一个程序中,经常有让我们判断一个集合中是否存在某个数的case;大多数情况下,只需要用map或是list这样简单的数据结构,如果使用的是高级语言,还能乘上快车调用几个封装好的api,加几个if else,两三行代码就可以在控制台看自己“完美”而又“健壮”的代码跑起来了。
但是,事无完美,在高并发环境下,所有的case都会极端化,如果这是一个十分庞大的集合(给这个庞大一个具体的值吧,一个亿),简单的一个hash map,不考虑链表所需的指针内存空间,一亿个int类型的整数,就需要380多M(4byte × 10 ^8),十亿的话就是4个G,不考虑性能,光算算这内存开销,即使现在满地都是128G的服务器,也不好吃下这一壶。
bitmap则使用位数代表数的大小,bit中存储的0或者1来标识该整数是否存在,具体模型如下:
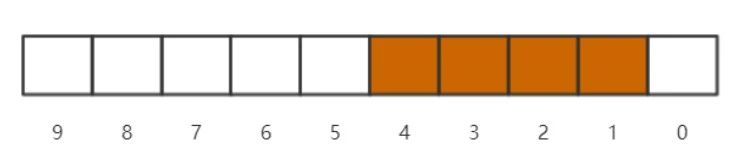
这是一个能标识0-9的“bitmap”,其中4321这四个数存在
计算一下bitmap的内存开销,如果是1亿以内的数据查找,我们只需要1亿个bit = 12MB左右的内存空间,就可以完成海量数据查找了,是不是极其诱人的一个内存缩减,以下为Java实现的bitmap代码:
public class MyBitMap {
private byte[] bytes;
private int initSize;
public MyBitMap(int size) {
if (size <= 0) {
return;
}
initSize = size / (8) + 1;
bytes = new byte[initSize];
}
public void set(int number) {
//相当于对一个数字进行右移动3位,相当于除以8
int index = number >> 3;
//相当于 number % 8 获取到byte[index]的位置
int position = number & 0x07;
//进行|或运算 参加运算的两个对象只要有一个为1,其值为1。
bytes[index] |= 1 << position;
}
public boolean contain(int number) {
int index = number >> 3;
int position = number & 0x07;
return (bytes[index] & (1 << position)) != 0;
}
public static void main(String[] args) {
MyBitMap myBitMap = new MyBitMap(32);
myBitMap.set(30);
myBitMap.set(13);
myBitMap.set(24);
System.out.println(myBitMap.contain(2));
}
}
使用简单的byte数组和位运算,就能做到时间与空间的完美均衡,是不是美美哒,wrong!试想一下,如果我们明确这是一个一亿以内,但是数量级只有10的集合,我们使用bitmap,同样需要开销12M的数据,如果是10亿以内的数据,开销就会涨到120M,bitmap的空间开销永远是和他的数据取值范围挂钩的,只有在海量数据下,他才能够大显身手。
再说说刚刚提到的那个极端case,假设这个数据量在一千万,但是取值范围好死不死就在十个亿以内,那我们不可避免还是要面对120M的开销,有方法应对么?
布隆过滤器
如果面对笔者说的以上问题,我们结合一下常规的解决方案,譬如说hash一下,我将十亿以内的某个数据,hash成一亿内的某个值,再去bitmap中查怎么样,如下图,布隆过滤器就是这么干的:
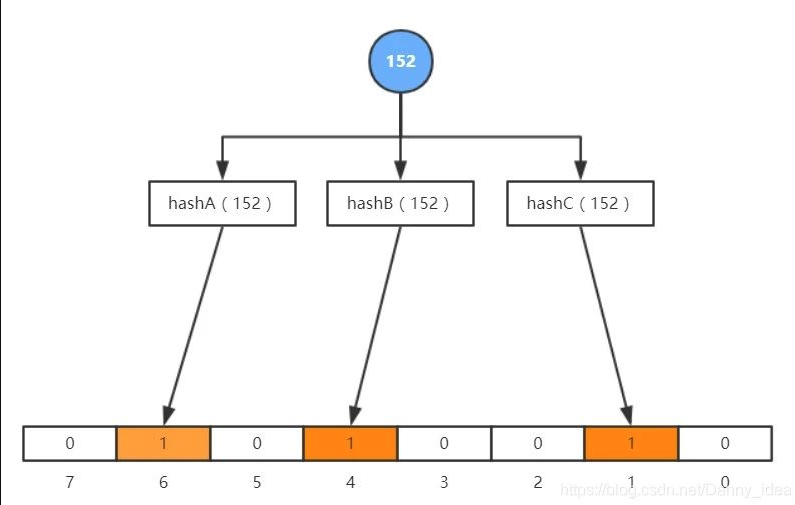
利用多个hash算法得到的值,减小hash碰撞的概率
像上面的图注所说,我们可以利用多个hash算法减小碰撞概率,但只要存在碰撞,就一定会有错误判断,我们无法百分百确定一个值是否真的存在,但是hash算法的魅力在于,我不能确定你是否存在,但是我可以确定你是否真的不存在,这也就是以上的实现为什么称之“过滤器”的原因了。