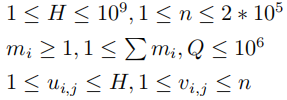JZOJ6642. 【GDOI20205.20模拟】classroom

Description

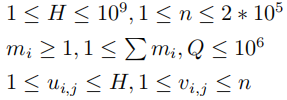
Solution

• 一道集大成的数据结构题。
• 假设$W(x)$表示$x$到最近的楼梯的距离。
• 根为$x$答案为——跨层的贡献，所有点到$x$的距离和，所有点到$x$路径上$Min(W(p))$的和。
• 第一个可以排序简单计算。
• 第二个可以虚树上换根DP。
• 第三个由于是最小值，可以考虑并查集。可以直接并查集然后打tag计算答案。也可以预先建出克鲁斯卡尔重构树（注意这里没有新加的点，从大到小加入，那么两点路径上的最小值就是它们的LCA的W），然后建虚树，再在上面换根DP。
• 注意到同层不需要走楼梯，所以用总的$sum Min()$减去同层的$sum Min()$。
• 亿点点细节。
• $O(n log n+m log m)$。
• 当然你可以通过离线的方式将所有排序以一种类似桶排的方式挂到树上，做到$O(m)$排序，以及预处理ST表$O(1)$求LCA，但是性价比太低了 。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define maxn 200005
#define maxm 1000005
#define maxp 20
#define ll long long 
using namespace std;

int H,n,m,Q,i,j,k,c[maxn],W[maxn],opr[maxm];
int em,e[maxn*2],nx[maxn*2],ls[maxn]; 
ll dis[maxn],F1[maxn],F2[maxn],ans;
struct node{int x,h;} a[maxm];
int cmp(node a,node b){return a.h<b.h||a.h==b.h&&a.x<b.x;}
int cmp1(int i,int j){return W[i]>W[j];}

void read(int &x){
	x=0; char ch=getchar();
	for(;ch<'0'||ch>'9';ch=getchar());
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
}

struct Graph{
	int em,e[maxn*2],nx[maxn*2],ls[maxn];
	void insert(int x,int y){
		em++; e[em]=y; nx[em]=ls[x]; ls[x]=em;
		em++; e[em]=x; nx[em]=ls[y]; ls[y]=em;
	}	
	
	int t,w,d[maxn],rt;
	void GetW(){
		rt=1;for(i=1;i<=n;i++) W[i]=-1;
		t=w=0; for(i=1;i<=n;i++) if (c[i]) d[++w]=i,W[i]=0;
		while (t<w){
			int x=d[++t];
			for(i=ls[x];i;i=nx[i]) if (W[e[i]]==-1)
				d[++w]=e[i],W[e[i]]=W[x]+1;
		}
	}
	
	int p[maxn],bz[maxn];
	void build();
	
	int totd,dfn[maxn],fa[maxn][maxp],dep[maxn],bz0[maxn];
	void DFS(int x,int p){
		fa[x][0]=p,dfn[x]=++totd,dep[x]=dep[p]+1;
		for(int i=1;i<maxp;i++) fa[x][i]=fa[fa[x][i-1]][i-1];
		for(int i=ls[x];i;i=nx[i]) if (e[i]!=p)
			DFS(e[i],x);
	}
	
	int getlca(int x,int y){
		if (dep[x]<dep[y]) swap(x,y);
		for(int i=maxp-1;i>=0;i--) if (dep[fa[x][i]]>=dep[y]) x=fa[x][i];
		if (x==y) return x;
		for(int i=maxp-1;i>=0;i--) if (fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
		return fa[x][0];
	}
	
	int em0,e0[maxn*2],nx0[maxn*2],ls0[maxn*2],B[maxn];
	void insert0(int x,int y){
		em0++; e0[em0]=y; nx0[em0]=ls0[x]; ls0[x]=em0;
		em0++; e0[em0]=x; nx0[em0]=ls0[y]; ls0[y]=em0;
	}
	
	int tp[maxn];
	void maketree(){
		em0=0,t=0,w=1,d[w]=rt,ls0[rt]=0,B[B[0]=1]=rt;
		for(int i=1;i<=opr[0];i++) if (opr[i]!=rt&&(i==1||opr[i]!=opr[i-1])){
			int p=opr[i],x=d[w],lca=getlca(x,p);
			if (lca==x) d[++w]=p,ls0[p]=0,B[++B[0]]=p; else {
				while (dfn[lca]<dfn[d[w-1]])
					insert0(d[w-1],d[w]),w--;
				if (dfn[lca]>dfn[d[w-1]]) {
					ls0[lca]=ls0[p]=0,insert0(lca,d[w]),w--;
					d[++w]=lca,d[++w]=p,B[++B[0]]=lca,B[++B[0]]=p;
				} else {
					insert0(d[w-1],d[w]),w--;
					ls0[p]=0,d[++w]=p,B[++B[0]]=p;
				}
			}
		}
		while (w>1) insert0(d[w-1],d[w]),w--;
		for(int i=1;i<=B[0];i++) tp[B[i]]=0;
		for(int i=1;i<=opr[0];i++) tp[opr[i]]=1;
	}
	
	ll f[maxn],sz[maxn];
	void DFS1(int x,int p){
		for(int i=ls0[x];i;i=nx0[i]) if (e0[i]!=p){
			DFS1(e0[i],x),f[x]+=f[e0[i]]+sz[e0[i]]*(dep[e0[i]]-dep[x]);
			sz[x]+=sz[e0[i]];
		}
	}
	
	void DFS2(int x,int p,ll sum){
		if (tp[x]) dis[x]=f[x]+sum;
		for(int i=ls0[x];i;i=nx0[i]) if (e0[i]!=p){
			int y=e0[i];
			DFS2(y,x,sum+f[x]-f[y]+1ll*(-sz[y]*2+opr[0])*(dep[y]-dep[x]));
		}
	}
	
	void dp1(){
		for(int i=1;i<=B[0];i++) f[B[i]]=sz[B[i]]=0;
		for(int i=1;i<=opr[0];i++) sz[opr[i]]++;
		DFS1(rt,0),DFS2(rt,0,0);
	}
	
	void DFS3(int x,int p,ll sum){
		if (tp[x]) F1[x]=(sz[x])*W[x]+sum;
		for(int i=ls0[x];i;i=nx0[i]) if (e0[i]!=p)
			DFS3(e0[i],x,sum+1ll*W[x]*(sz[x]-sz[e0[i]]));
	}
	
	void dp2(){
		for(int i=1;i<=B[0];i++) f[B[i]]=sz[B[i]]=0;
		for(int i=1;i<=opr[0];i++) sz[opr[i]]++;
		DFS1(rt,0);
		DFS3(rt,0,0);
	}
} G,T;

int fat[maxn];
int father(int x){return (fat[x]==x)?x:fat[x]=father(fat[x]);}
void Graph::build(){
	for(i=1;i<=n;i++) p[i]=i,fat[i]=i;
	sort(p+1,p+1+n,cmp1);
	for(i=1;i<=n;i++){
		int x=p[i]; 
		bz[x]=1;
		for(j=G.ls[x];j;j=G.nx[j]) if (bz[G.e[j]]){
			insert(x,father(G.e[j]));
			fat[father(G.e[j])]=x;
		}
	}
	rt=p[n];
}

int cmpG(int i,int j){return G.dfn[i]<G.dfn[j];}
int cmpT(int i,int j){return T.dfn[i]<T.dfn[j];}

ll pres[maxm],nexs[maxm];

int main(){
	read(H),read(n);
	for(i=1;i<=n;i++) read(c[i]);
	for(i=1;i<n;i++) read(j),read(k),G.insert(j,k);
	G.GetW(),G.DFS(1,0);
	T.build(),T.DFS(T.rt,0);
	read(Q);
	while (Q--){
		read(m);
		for(i=1;i<=m;i++) read(a[i].h),read(a[i].x);
		sort(a+1,a+1+m,cmp);
		pres[1]=nexs[m]=0;
		for(i=2;i<=m;i++) pres[i]=pres[i-1]+1ll*(a[i].h-a[i-1].h)*(i-1);
		for(i=m-1;i>=1;i--) nexs[i]=nexs[i+1]+1ll*(a[i+1].h-a[i].h)*(m-i);
		
		opr[0]=m;for(i=1;i<=m;i++) opr[i]=a[i].x;
		sort(opr+1,opr+1+opr[0],cmpG),G.maketree(),G.dp1();
		sort(opr+1,opr+1+opr[0],cmpT),T.maketree(),T.dp2();
		for(i=1;i<=opr[0];i++) F2[opr[i]]=F1[opr[i]];
		
		ans=1e18;
		for(i=1;i<=m;i=j){
			for(j=i;a[j].h==a[i].h&&j<=m;j++);
			opr[0]=0;for(k=i;k<j;k++) opr[++opr[0]]=a[k].x;
			sort(opr+1,opr+1+opr[0],cmpT),T.maketree(),T.dp2();
			for(k=i;k<j;k++) 
				ans=min(ans,pres[k]+nexs[k]+dis[a[k].x]+(F2[a[k].x]-F1[a[k].x])*2);
		}
		printf("%lld
",ans);
	}
}