The Universal Function for n-ary computable functions is the (n+1)-ary function:
$psi_U^{(n)}(e,x_1,...,x_n)simeqphi_e^{(n)}(x_1,...,x_n)$
Theorem. For each $n$, the universal function $psi_U$ is computable.
To avoid using Church's Thesis, we prove this theorem step by step in a top-down way as the following sketch.
Step 1. The configuration of the registers can be coded as $c=prod_{i>0}p_i^{r_i}$i, where $p_i$ is the ith prime, and given the number of the next instruction $j$ we can encode the current computation state as $sigma=pi(c,j)$. To prove the universal functions are computable, we should prove no further than $c_n(e,vec{x},t)$ and $j_n(e,vec{x},t)$ are computable since:
![]()
And we can prove that by proving the following function is a primitive recursive function (a stronger conclusion):
![]()
Step 2. From another perspective, $sigma_n$ can be defined as follow:

Hence, we need to prove config and next are primitive recursive functions.
Step 3. We further define the following auxillary functions:

And we should prove the functions above are primitive recursive due to the following facts:

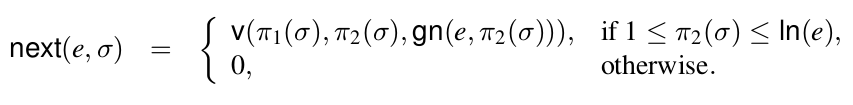
Step 4. To prove $ln$, $gn$, $ch$ and $v$ are primitive recursive functions, we should resort to the definitions of program code nunber and instruction code number. Here, I shall omit further details of the proof of this step.
Corollary 1. For each $n$, the following predicates are decidable:
(1) $S_n(e,vec{x},y,t)$ defined as $P_e(vec{x})$ converges to $y$ in $t$ or fewer steps;
(2) $H_n(e,vec{x},t)$ defined as $P_e(vec{x})$ converges in $t$ or fewer steps.
Corollary 2. (Kleene's normal form theorem) There is a total computable function $U(vec{x})$ and a decidable predicate $T_n(e,vec{x},z)$ such that:
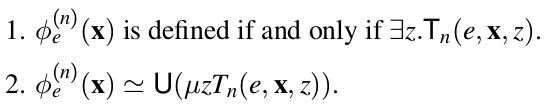
As a matter of fact, every computable function can be obtained from primitive recursive functions by using at most one application of the unbounded minimalisation.
Application 1. The problem '$phi_x$ is total' is undecidable.
To see this, we can construct a unary function defined by cases based on this predicate, which is other than any $phi_e(x)$ for any $e$ by using Cantor's Diagonal Argument.
This can also be deduced from the Rice's Theorem. A further conclusion would be whether a function is extensible to a total function is undecidable. For example, you cannot decide whether $f(x)=psi_U(x,x)+1$ is extensible, otherwise $xin W_x$ is decidable (see more about decidability).
As a matter of fact, we shall also see that this preidcate is not partially decidable in the near future.
Application 2. There is a total computable function that is not primitive recursive.
Here, we provide a proof sketch:

Application 3. (Effectiveness of Production)
There is a total computable function $s(x,y)$ such that $phi_{s(x,y)}=phi_xphi_y$ for all $x$ and $y$.
Application 4. (Effectiveness of Inverse)
There is a computable function such that:
1. $g(x,y)$ is defined if and only if $y in E_x$, and
2. if $yin E_x$, then $g(x,y)in W_x$ and $phi_x(g(x,y))=y$.
Application 5. (Effectiveness of Recursion)
Consider function $f$ defined by the following recursion:
![]()
![]()
There is a total computable function $r(e_1,e_2)$ such that:
![]()
References:
1. Cutland, Nigel. Computability: an introduction to recursive function theory[M]. Cambridge: Cambridge University Press, 1980