zoukankan      html  css  js  c++  java

  • Codeforces Round #521 (Div. 3)

    题目链接：http://codeforces.com/contest/1077

    A题：

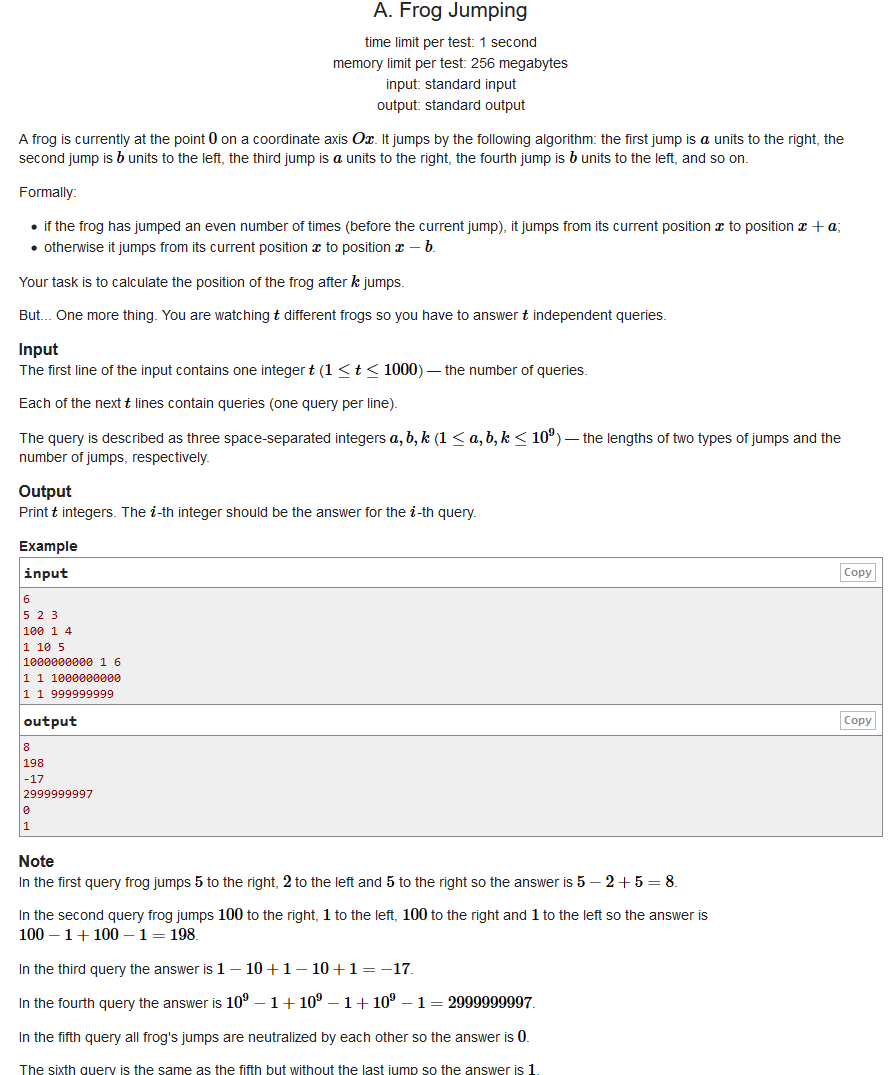
    题意：

    　　一只青蛙站在0处向左右跳动，奇数次跳动是向右跳动a个单位，偶数次为向左跳动b个单位，求k次跳动后他在哪里。

    思路：

    　　看k的奇偶即可。

    代码实现如下：

     1 #include <set>
 2 #include <map>
 3 #include <queue>
 4 #include <stack>
 5 #include <cmath>
 6 #include <ctime>
 7 #include <bitset>
 8 #include <cstdio>
 9 #include <string>
10 #include <vector>
11 #include <cstdlib>
12 #include <cstring>
13 #include <iostream>
14 #include <algorithm>
15 using namespace std;
16 
17 typedef long long LL;
18 typedef pair<LL, LL> pLL;
19 typedef pair<LL, int> pli;
20 typedef pair<int, LL> pil;;
21 typedef pair<int, int> pii;
22 typedef unsigned long long uLL;
23 
24 #define lson rt<<1
25 #define rson rt<<1|1
26 #define lowbit(x) x&(-x)
27 #define  name2str(name) (#name)
28 #define bug printf("*********
")
29 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
30 #define FIN freopen("D://code//in.txt", "r", stdin)
31 #define IO ios::sync_with_stdio(false),cin.tie(0)
32 
33 const double eps = 1e-8;
34 const int mod = 1000000007;
35 const int maxn = 4e4 + 7;
36 const double pi = acos(-1);
37 const int inf = 0x3f3f3f3f;
38 const LL INF = 0x3f3f3f3f3f3f3f3fLL;
39 
40 int t;
41 LL a, b, k;
42 
43 int main() {
44     scanf("%d", &t);
45     while(t--) {
46         scanf("%lld%lld%lld", &a, &b, &k);
47         LL tmp = k / 2;
48         if(k & 1) {
49             printf("%lld
", tmp * (a - b) + a);
50         } else {
51             printf("%lld
", tmp * (a - b));
52         }
53     }
54     return 0;
55 }
    View Code

    B题：

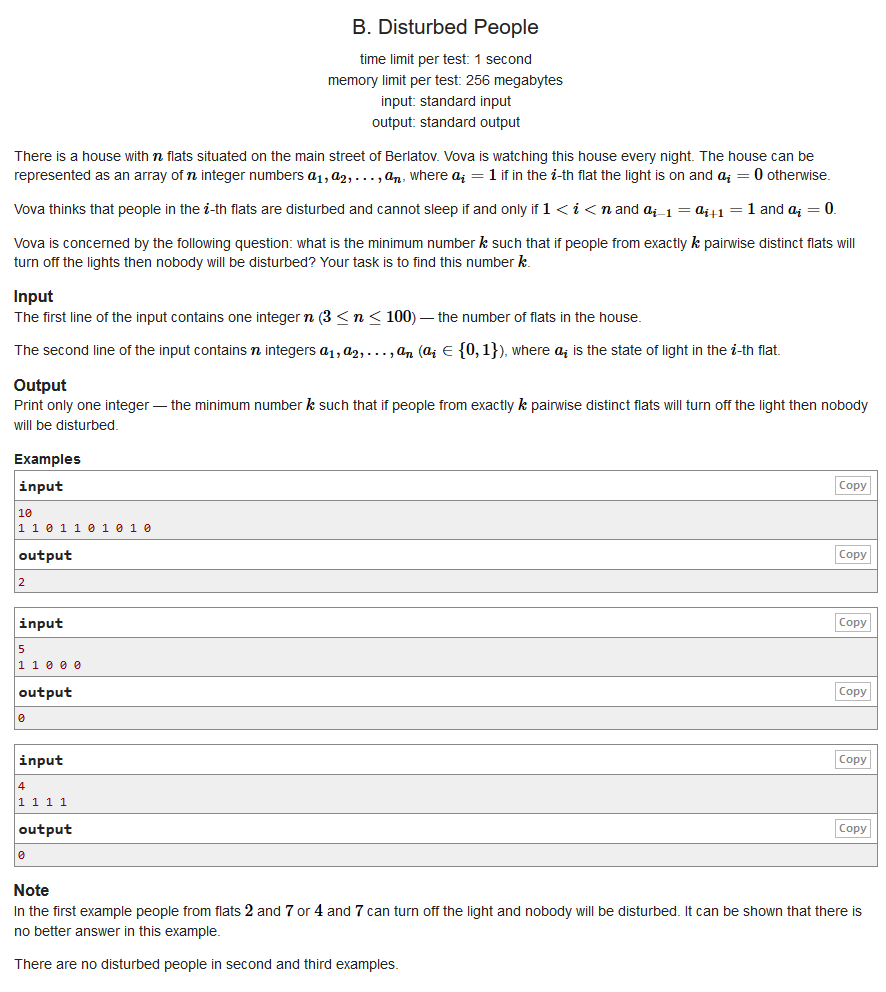
    题意：

    　　给你长度为n的01数组，你可以将1变成0，问使得数组中没有101这样的连续段的最少操作次数。

    思路：

    　　对于每个101中的0，只需要将这个0后面的那个1变成0即可，易知此方案最优。

    代码实现如下：

     1 #include <set>
 2 #include <map>
 3 #include <queue>
 4 #include <stack>
 5 #include <cmath>
 6 #include <ctime>
 7 #include <bitset>
 8 #include <cstdio>
 9 #include <string>
10 #include <vector>
11 #include <cstdlib>
12 #include <cstring>
13 #include <iostream>
14 #include <algorithm>
15 using namespace std;
16 
17 typedef long long LL;
18 typedef pair<LL, LL> pLL;
19 typedef pair<LL, int> pli;
20 typedef pair<int, LL> pil;;
21 typedef pair<int, int> pii;
22 typedef unsigned long long uLL;
23 
24 #define lson rt<<1
25 #define rson rt<<1|1
26 #define lowbit(x) x&(-x)
27 #define  name2str(name) (#name)
28 #define bug printf("*********
")
29 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
30 #define FIN freopen("D://code//in.txt", "r", stdin)
31 #define IO ios::sync_with_stdio(false),cin.tie(0)
32 
33 const double eps = 1e-8;
34 const int mod = 1000000007;
35 const int maxn = 2e5 + 7;
36 const double pi = acos(-1);
37 const int inf = 0x3f3f3f3f;
38 const LL INF = 0x3f3f3f3f3f3f3f3fLL;
39 
40 int n;
41 int a[maxn];
42 
43 int main() {
44     scanf("%d", &n);
45     for(int i = 1; i <= n; i++) {
46         scanf("%d", &a[i]);
47     }
48     int ans = 0;
49     for(int i = 2; i < n; i++) {
50         if(a[i] == 0 && a[i-1] == 1 && a[i+1] == 1) {
51             ans++;
52             a[i+1] = 0;
53         }
54     }
55     printf("%d
", ans);
56     return 0;
57 }
    View Code

    C题：

    题意：

    　　给你大小为n个数组，求删除一个数后使得剩下的n-1个数中有一个数等于其余数的和的位置的集合。

    思路：

    　　这题虽然可以直接模拟，但是我看到这个题的时候第一想法就是线段树维护区间和与区间最大值，对于每个位置现将这个位置置为0，然后查询区间和是否等于2*最大值，然后再把这个位置改回去。

    代码实现如下：

     1 #include <set>
 2 #include <map>
 3 #include <queue>
 4 #include <stack>
 5 #include <cmath>
 6 #include <ctime>
 7 #include <bitset>
 8 #include <cstdio>
 9 #include <string>
10 #include <vector>
11 #include <cstdlib>
12 #include <cstring>
13 #include <iostream>
14 #include <algorithm>
15 using namespace std;
16 
17 typedef long long LL;
18 typedef pair<LL, LL> pLL;
19 typedef pair<LL, int> pli;
20 typedef pair<int, LL> pil;;
21 typedef pair<int, int> pii;
22 typedef unsigned long long uLL;
23 
24 #define lson rt<<1
25 #define rson rt<<1|1
26 #define lowbit(x) x&(-x)
27 #define  name2str(name) (#name)
28 #define bug printf("*********
")
29 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
30 #define FIN freopen("D://code//in.txt", "r", stdin)
31 #define IO ios::sync_with_stdio(false),cin.tie(0)
32 
33 const double eps = 1e-8;
34 const int mod = 1000000007;
35 const int maxn = 2e5 + 7;
36 const double pi = acos(-1);
37 const int inf = 0x3f3f3f3f;
38 const LL INF = 0x3f3f3f3f3f3f3f3fLL;
39 
40 int n;
41 int a[maxn];
42 
43 struct node {
44     int l, r, mx;
45     LL sum;
46 }segtree[maxn<<2];
47 
48 void push_up(int rt) {
49     segtree[rt].sum = segtree[lson].sum + segtree[rson].sum;
50     segtree[rt].mx = max(segtree[lson].mx, segtree[rson].mx);
51 }
52 
53 void build(int rt, int l, int r) {
54     segtree[rt].l = l, segtree[rt].r = r;
55     if(l == r) {
56         segtree[rt].sum = segtree[rt].mx = a[l];
57         return;
58     }
59     int mid = (l + r) >> 1;
60     build(lson, l, mid);
61     build(rson, mid + 1, r);
62     push_up(rt);
63 }
64 
65 void update(int rt, int pos, int val) {
66     if(segtree[rt].l == segtree[rt].r) {
67         segtree[rt].mx = segtree[rt].sum = val;
68         return;
69     }
70     int mid = (segtree[rt].l + segtree[rt].r) >> 1;
71     if(pos <= mid) update(lson, pos, val);
72     else update(rson, pos, val);
73     push_up(rt);
74 }
75 
76 vector<int> v;
77 
78 int main() {
79     scanf("%d", &n);
80     for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
81     build(1, 1, n);
82     for(int i = 1; i <= n; i++) {
83         int x = a[i];
84         update(1, i, 0);
85         if(segtree[1].sum == 2 * segtree[1].mx) v.push_back(i);
86         update(1, i, x);
87     }
88     printf("%d
", v.size());
89     for(int i = 0; i < (int)v.size(); i++) {
90         printf("%d ", v[i]);
91     }
92     printf("
");
93     return 0;
94 }
    View Code

    D题：

    题意：

    　　给你大小为n个数组，求一个长度为k的序列（可以不连续）使得它在原数组中出现次数最多。

    思路：

    　　记录每个元素出现次数，然后二分出现次数。

    代码实现如下：

     1 #include <set>
 2 #include <map>
 3 #include <queue>
 4 #include <stack>
 5 #include <cmath>
 6 #include <ctime>
 7 #include <bitset>
 8 #include <cstdio>
 9 #include <string>
10 #include <vector>
11 #include <cstdlib>
12 #include <cstring>
13 #include <iostream>
14 #include <algorithm>
15 using namespace std;
16 
17 typedef long long LL;
18 typedef pair<LL, LL> pLL;
19 typedef pair<LL, int> pli;
20 typedef pair<int, LL> pil;;
21 typedef pair<int, int> pii;
22 typedef unsigned long long uLL;
23 
24 #define lson rt<<1
25 #define rson rt<<1|1
26 #define lowbit(x) x&(-x)
27 #define  name2str(name) (#name)
28 #define bug printf("*********
")
29 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
30 #define FIN freopen("D://code//in.txt", "r", stdin)
31 #define IO ios::sync_with_stdio(false),cin.tie(0)
32 
33 const double eps = 1e-8;
34 const int mod = 1000000007;
35 const int maxn = 2e5 + 7;
36 const double pi = acos(-1);
37 const int inf = 0x3f3f3f3f;
38 const LL INF = 0x3f3f3f3f3f3f3f3fLL;
39 
40 int n, k;
41 int a[maxn], num[maxn];
42 
43 bool check(int x) {
44     int cnt = 0;
45     for(int i = 1; i < maxn; i++) {
46         cnt += num[i] / x;
47     }
48     return cnt >= k;
49 }
50 
51 int main() {
52     scanf("%d%d", &n, &k);
53     for(int i = 1; i <= n; i++) {
54         scanf("%d", &a[i]);
55         num[a[i]]++;
56     }
57     int ub = maxn, lb = 1, mid;
58     while(ub >= lb) {
59         mid = (ub + lb) >> 1;
60         if(check(mid)) {
61             lb = mid + 1;
62         } else {
63             ub = mid - 1;
64         }
65     }
66     int cnt = 0;
67     for(int i = 1; i < maxn; i++) {
68         if(cnt >= k) break;
69         while(num[i] >= ub) {
70             printf("%d ", i);
71             cnt++;
72             if(cnt >= k) break;
73             num[i] -= ub;
74         }
75     }
76     printf("
");
77     return 0;
78 }
    View Code

    E题：

    题意：

    　　有n个题目，有相同的题目也有不同的，问满足以下条件的安排使用的最大元素个数：

    　　　　1.每一场比赛的题目必须相同；

    　　　　2.不同场的比赛题目不能相同；

    　　　　3.第二场的题目数是第一场的两倍，第三场是第二场的两倍……

    思路：

    　　枚举第一场比赛所需要的题目数，然后二分查找即可。

    代码实现如下：

     1 #include <set>
 2 #include <map>
 3 #include <queue>
 4 #include <stack>
 5 #include <cmath>
 6 #include <ctime>
 7 #include <bitset>
 8 #include <cstdio>
 9 #include <string>
10 #include <vector>
11 #include <cstdlib>
12 #include <cstring>
13 #include <iostream>
14 #include <algorithm>
15 using namespace std;
16 
17 typedef long long LL;
18 typedef pair<LL, LL> pLL;
19 typedef pair<LL, int> pli;
20 typedef pair<int, LL> pil;;
21 typedef pair<int, int> pii;
22 typedef unsigned long long uLL;
23 
24 #define lson rt<<1
25 #define rson rt<<1|1
26 #define lowbit(x) x&(-x)
27 #define  name2str(name) (#name)
28 #define bug printf("*********
")
29 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
30 #define FIN freopen("D://code//in.txt", "r", stdin)
31 #define IO ios::sync_with_stdio(false),cin.tie(0)
32 
33 const double eps = 1e-8;
34 const int mod = 1000000007;
35 const int maxn = 2e5 + 7;
36 const double pi = acos(-1);
37 const int inf = 0x3f3f3f3f;
38 const LL INF = 0x3f3f3f3f3f3f3f3fLL;
39 
40 int n, sz;
41 LL ans;
42 int a[maxn], num[maxn];
43 vector<int> v;
44 
45 void solve(int x) {
46     int tmp = x, tt = 0;
47     LL sum = 0;
48     while(1) {
49         int pos = lower_bound(num + tt, num + sz, tmp) - num;
50         if(pos >= sz) break;
51         sum += tmp;
52         tmp *= 2;
53         tt = pos + 1;
54     }
55     ans = max(ans, sum);
56 }
57 
58 int main() {
59     scanf("%d", &n);
60     for(int i = 1; i <= n; i++) {
61         scanf("%d", &a[i]);
62         v.push_back(a[i]);
63     }
64     sort(v.begin(), v.end());
65     v.erase(unique(v.begin(), v.end()), v.end());
66     sz = v.size();
67     for(int i = 1; i <= n; i++) {
68         a[i] = lower_bound(v.begin(), v.end(), a[i]) - v.begin();
69         num[a[i]]++;
70     }
71     sort(num, num + sz);
72     for(int i = 1; i <= num[sz-1]; i++) {
73         solve(i);
74     }
75     printf("%lld
", ans);
76     return 0;
77 }
    View Code

    F题：

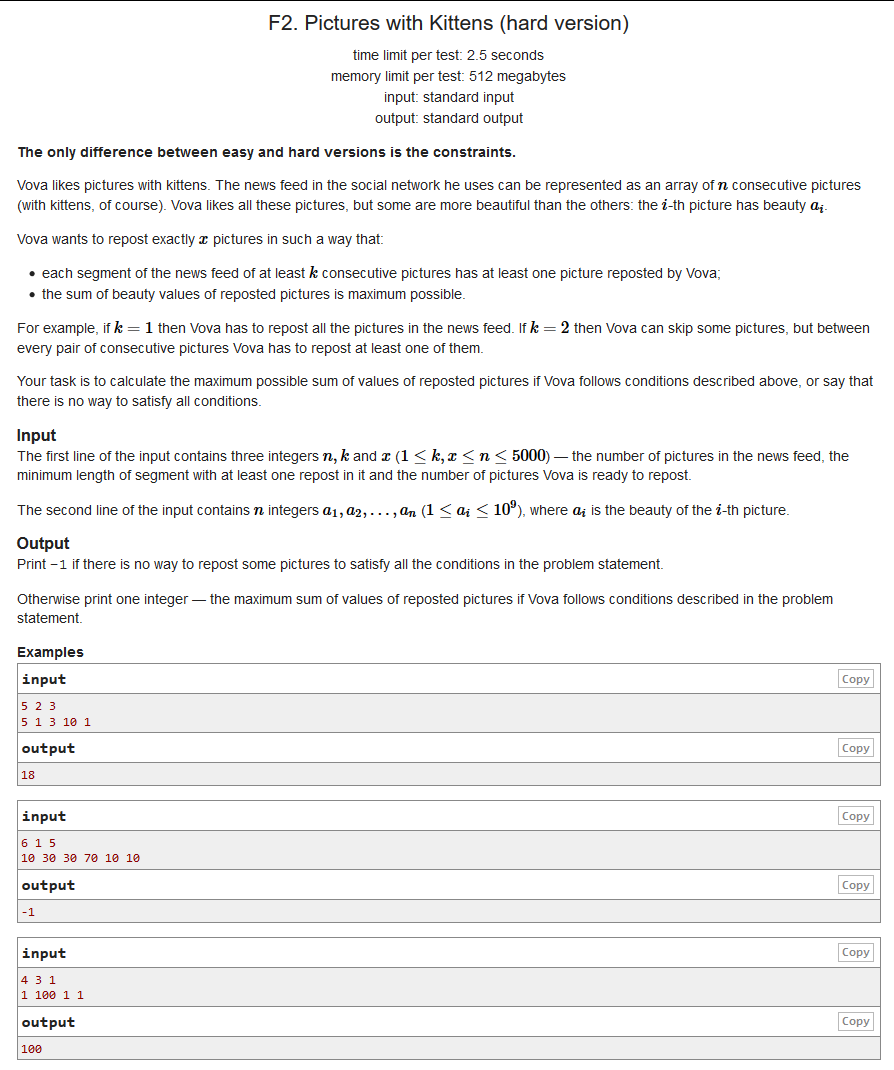
    题意：

    　　有长度为n个数组，要求选择x个元素，但是你所选择的相邻两个元素间的距离不能大于等于k，求最大值。

    思路：

    　　F1和F2题目相同，但是F2的数据范围要大，这个是div3的习惯套路。

    　　我们记dp[i][j]为前i个元素选择j个元素的最大值，转移方程为dp[i][j]=max{dp[t][j-1]}，其中i-k<=t<i。

    　　F1中n，k，x都是小于等于200的，因此可以暴力dp，而F2则需要使用优先队列/单调队列优化dp（优先队列优化比单调队列优化慢10倍）。

    代码实现如下：

    F1的O(n*k*x)暴力dp：

     1 #include <set>
 2 #include <map>
 3 #include <queue>
 4 #include <stack>
 5 #include <cmath>
 6 #include <ctime>
 7 #include <bitset>
 8 #include <cstdio>
 9 #include <string>
10 #include <vector>
11 #include <cstdlib>
12 #include <cstring>
13 #include <iostream>
14 #include <algorithm>
15 using namespace std;
16 
17 typedef long long LL;
18 typedef pair<LL, LL> pLL;
19 typedef pair<LL, int> pli;
20 typedef pair<int, LL> pil;;
21 typedef pair<int, int> pii;
22 typedef unsigned long long uLL;
23 
24 #define lson rt<<1
25 #define rson rt<<1|1
26 #define lowbit(x) x&(-x)
27 #define  name2str(name) (#name)
28 #define bug printf("*********
")
29 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
30 #define FIN freopen("D://code//in.txt", "r", stdin)
31 #define IO ios::sync_with_stdio(false),cin.tie(0)
32 
33 const double eps = 1e-8;
34 const int mod = 1000000007;
35 const int maxn = 200 + 7;
36 const double pi = acos(-1);
37 const int inf = 0x3f3f3f3f;
38 const LL INF = 0x3f3f3f3f3f3f3f3fLL;
39 
40 int n, k, x;
41 int a[maxn];
42 LL dp[maxn][maxn];
43 
44 int main() {
45     scanf("%d%d%d", &n, &k, &x);
46     for(int i = 1; i <= n; i++) {
47         scanf("%d", &a[i]);
48     }
49     memset(dp, 128, sizeof(dp));
50     dp[0][0] = 0;
51     for (int i = 1; i <= n; i++) {
52         for (int j = i - k; j < i; j++) {
53             if(j < 0) continue;
54             for (int l = 1; l <= x; l++)
55                 dp[i][l] = max(dp[j][l-1] + a[i], dp[i][l]);
56         }
57     }
58     LL ans = -1;
59     for (int i = n - k + 1; i <= n; i++)
60         if(dp[i][x]>0) ans = max(ans, dp[i][x]);
61     printf("%lld
", ans);
62     return 0;
63 }
    View Code

    优先队列优化dp：

     1 #include <set>
 2 #include <map>
 3 #include <deque>
 4 #include <queue>
 5 #include <stack>
 6 #include <cmath>
 7 #include <ctime>
 8 #include <bitset>
 9 #include <cstdio>
10 #include <string>
11 #include <vector>
12 #include <cstdlib>
13 #include <cstring>
14 #include <iostream>
15 #include <algorithm>
16 using namespace std;
17 
18 typedef long long LL;
19 typedef pair<LL, LL> pLL;
20 typedef pair<LL, int> pli;
21 typedef pair<int, LL> pil;;
22 typedef pair<int, int> pii;
23 typedef unsigned long long uLL;
24 
25 #define lson rt<<1
26 #define rson rt<<1|1
27 #define lowbit(x) x&(-x)
28 #define  name2str(name) (#name)
29 #define bug printf("*********
")
30 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
31 #define FIN freopen("D://code//in.txt", "r", stdin)
32 #define IO ios::sync_with_stdio(false),cin.tie(0)
33 
34 const double eps = 1e-8;
35 const int mod = 1000000007;
36 const int maxn = 5e3 + 7;
37 const double pi = acos(-1);
38 const int inf = 0x3f3f3f3f;
39 const LL INF = 0x3f3f3f3f3f3f3f3fLL;
40 
41 int n, k, x;
42 int a[maxn];
43 
44 priority_queue<pli> q[maxn];
45 
46 int main() {
47     scanf("%d%d%d", &n, &k, &x);
48     for(int i = 1; i <= n; i++) {
49         scanf("%d", &a[i]);
50     }
51     LL ans = -1;
52     q[0].push(make_pair(0, 0));
53     for(int i = 1; i <= n; i++) {
54         for(int j = x; j >= 1; j--) {
55             while(!q[j-1].empty() && q[j-1].top().second < i - k) q[j-1].pop();
56             if(q[j-1].empty()) continue;
57             LL val = q[j-1].top().first + a[i];
58             q[j].push(make_pair(val, i));
59             if(n - k < i && j == x) ans = max(ans, val);
60         }
61     }
62     printf("%lld
", ans);
63     return 0;
64 }
    View Code

    单调队列优化dp：

     1 #include <set>
 2 #include <map>
 3 #include <deque>
 4 #include <queue>
 5 #include <stack>
 6 #include <cmath>
 7 #include <ctime>
 8 #include <bitset>
 9 #include <cstdio>
10 #include <string>
11 #include <vector>
12 #include <cstdlib>
13 #include <cstring>
14 #include <iostream>
15 #include <algorithm>
16 using namespace std;
17 
18 typedef long long LL;
19 typedef pair<LL, LL> pLL;
20 typedef pair<LL, int> pli;
21 typedef pair<int, LL> pil;;
22 typedef pair<int, int> pii;
23 typedef unsigned long long uLL;
24 
25 #define lson rt<<1
26 #define rson rt<<1|1
27 #define lowbit(x) x&(-x)
28 #define  name2str(name) (#name)
29 #define bug printf("*********
")
30 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
31 #define FIN freopen("D://code//in.txt", "r", stdin)
32 #define IO ios::sync_with_stdio(false),cin.tie(0)
33 
34 const double eps = 1e-8;
35 const int mod = 1000000007;
36 const int maxn = 5e3 + 7;
37 const double pi = acos(-1);
38 const int inf = 0x3f3f3f3f;
39 const LL INF = 0x3f3f3f3f3f3f3f3fLL;
40 
41 int n, k, x;
42 int a[maxn];
43 
44 deque<pli> q[maxn];
45 
46 int main() {
47     scanf("%d%d%d", &n, &k, &x);
48     for(int i = 1; i <= n; i++) {
49         scanf("%d", &a[i]);
50     }
51     LL ans = -1;
52     q[0].push_back(make_pair(0, 0));
53     for(int i = 1; i <= n; i++) {
54         for(int j = x; j >= 1; j--) {
55             while(!q[j-1].empty() && q[j-1].front().second < i - k) q[j-1].pop_front();
56             if(q[j-1].empty()) continue;
57             LL val = q[j-1].front().first + a[i];
58             if(n - k < i && j == x) ans = max(ans, val);
59             while(!q[j].empty() && q[j].back().first <= val) q[j].pop_back();
60             q[j].push_back(make_pair(val, i));
61         }
62     }
63     printf("%lld
", ans);
64     return 0;
65 }
    View Code
  • 相关阅读:
    ios NSFileHandle
    ios NSString crash
    触摸方法
    代理中方法
    初始化时加载的方法
    [leetCode]209. 长度最小的子数组
    [leetCode]669. 修剪二叉搜索树
    [leetCode]763. 划分字母区间
    7.Jedis
    6.Redis事务（乐观锁）
  • 原文地址：https://www.cnblogs.com/Dillonh/p/9974636.html
Copyright © 2011-2022 走看看