这是一道非常经典的模版题,做法万变不离其宗,但是还是有不少可记叙的。
法一:值域线段树套序列线段树
这应该是见得很多的做法了,也是我最先写的做法。值域线段树上每个结点都对应了一棵序列线段树,值域线段树线段[lf,rg]上序列线段树线段[L,R]的值表示[L,R]这段区间有多少个值域在[lf,rg]之间的值。
修改时,因为是[l,r]每个位置都添入了权值c。于是就是值域线段树走到c,中间每个线段[l,r]加上r-l+1。
查询时,就当是二分答案,答案区间就是值域线段树的线段,每次取右儿子,看当前区间在右儿子值域中出现的数的个数,与k比较。如果k不足则向右走,否则向左走而且k相应减小。
于是这样下来,一个常数巨大的树套树就出来了,时间复杂度O(nlog2n),空间复杂度O(nlog2n)。我最开始是,内存池300*N,241080 kb,12872 ms。
确实太慢了。考虑优化,内层其实完全可以标记永久化,不用pushdown,一些多余结点的浪费也随之消失。内存池200*N,201236 kb,7852 ms。
但这还不够,考虑到值域线段树所有的左儿子其实都没有用,于是在修改时可以直接跳过,时空复杂度更小。内存池100*N,101624 kb,5556 ms。
法二:整体二分套序列树状数组
整体二分这个方法让我迷乱了好久,最后才发现,其实就只是没有建出值域线段树而已。所有的操作的时间相对顺序不变,solve(lf,rg,...)表示...这些操作都滚到了[lf,rg]这条线段上。于是我们只需要按照顺序做,把相应的操作都丢到更下面的线段去。
而很明显,在这种情况下线段树只留一棵也行。每一次处理完[lf,rg]的操作后,再把它清零。考虑线段树的操作,区间加一个数,询问区间的和。那这样,动态开点线段树就可以冬眠了~因为树状数组可以区修区询啊!
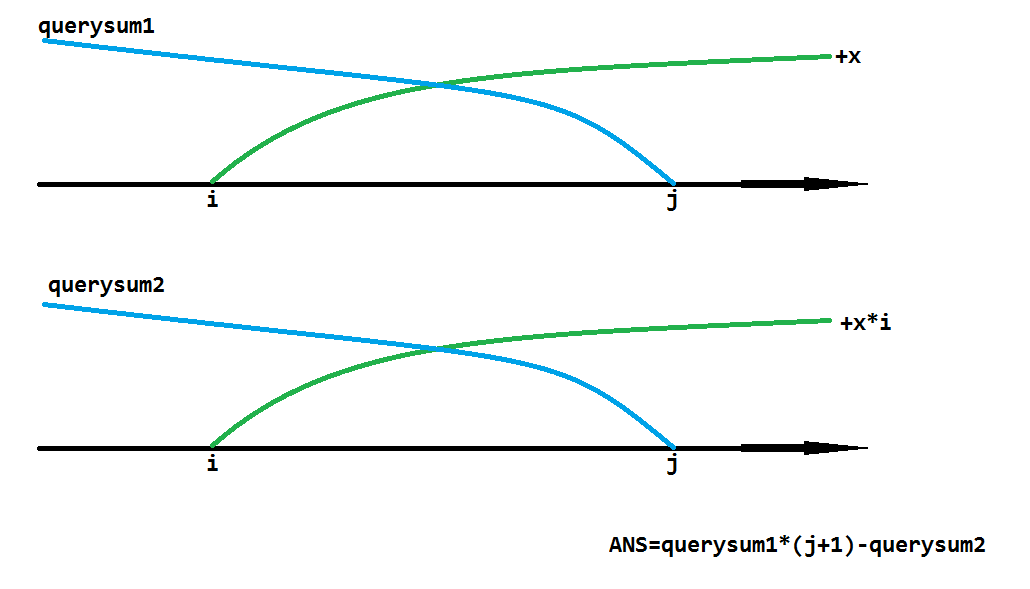
具体来说是这样的。如果说我让后缀[i,n]的所有位置都+x,之后询问前缀[1,j]的和,那很明显+x对询问的贡献就是x*(j-i+1)=x*(j+1)-x*i。而前面一半x*(j+1),宏观下来就是(Σx)*(j+1)。后面一半x*i,则是只与修改有关而与询问无关。当然,中间要求i<j。
于是,做法出来了:使用两棵序列树状数组。
Succeed!时间复杂度O(nlog2n),空间复杂度O(n)。3384 kb,1176 ms!!!
法三:序列树状数组套值域线段树
由法二的启迪,想到这个做法也不是特别困难。外层的树状数组也可以使用同样套路区间修改,而查询的时候则可以把若干个这样的根拿来一起跳,加加减减。
他们总说这是主席树,Too Young Too Simple!
最终时间复杂度O(nlog2n),空间复杂度O(nlog2n),跑下来效率还可以,内存池200*N,118652 kb,4852 ms。
法四:序列线段树套值域线段树
既然脑洞已经大开,那就怕是关不住了。修改的时候如果标记永久化,查询时再把若干个结点一起拿出来还加权,效果又会怎么样呢?
当然是可以的,写起来特别有意思。
时间复杂度O(nlog2n),空间复杂度O(nlog2n)。内存池300*N,182112 kb,6536 ms。
总结
这道题目做了我很久,但其实各种做法都差不多。然而,编程复杂度各不相同,所耗内存各不相同,时间也各不相同。是为什么呢?还是在于对题目的充分把握,还是在于对于数据结构本身的理解。
像法三和法四关系如此,而法一却不用序列树状数组,是因为要动态开点。同理,法三和法四也不能使用值域树状数组,除非你实在无聊把树状数组变成线段树然后再来跳。而法一不使用值域树状数组是因为不方便二分,而其实最后我们只留了右儿子,这其实本质上就是树状数组了。最后一句话比较玄妙,但很有意思。
而法四不能用vector存标记之后pushdown,因为我可以很轻松的卡掉。例如,n=25000,m=50000,前25000次操作中的第i次是1 1 25000 i,后25000次操作中的第i次是1 i i 1,就这样,空间飙到了O(n2)。而法一则可以pushdown,是因为有值的结点几乎都是要访问的结点。就是这样的差别。