二分图染色(弱化版)-牛客每日一题

题目链接：https://ac.nowcoder.com/acm/problem/13229

题意：

给定一个完全二分图，图的左右两边的顶点数目相同。

要给图中的每条边染成红色、蓝色、或者绿色，并使得任意两条红边不共享端点、同时任意两条蓝边也不共享端点。

计算所有满足条件的染色的方案数，并对10^9+7取模。

思路：

绿色可以看做不存在；

首先看只有红色的情况：用 (F_i) 表示二分图的一边有 i 个点的染色方案数。

• 显然 (f_0 = 1, f_1 = 2);

• 由 (f_{i - 1} o f_i), 图上会增加两个点.

• 如果两个点没有红线的出度，就是 (1 * f_{i - 1}) 种；

  

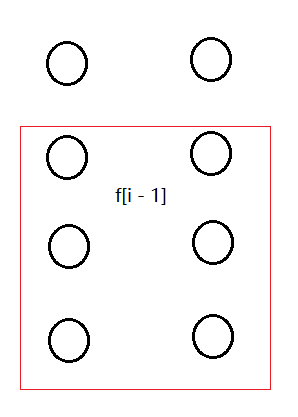
• 如果两个点之间是红线，和其他的点不连，也是 (1 * f_{i - 1})种；

  

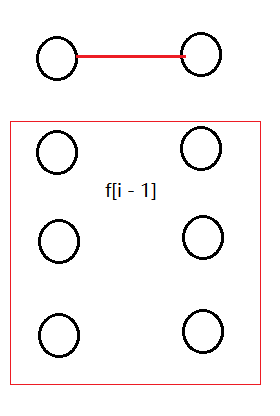
• 如果两个点只有其中一个点和之前的点连线，是 (2 * (i - 1) * f_{i - 1})种；

  

  但是这样会出现有的情况不符合，与题意不符，例如：

  

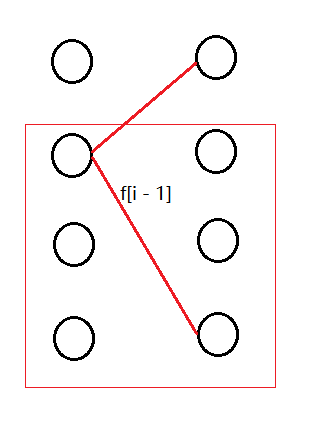
  这样的情况是 (2 * (i - 1) * (i - 1) * f_{i - 2}) 种，要减去；

• 如果两个点都和之前的点连线，有 ((i - 1) * (i - 1) * f_{i - 2}) 种情况；

  

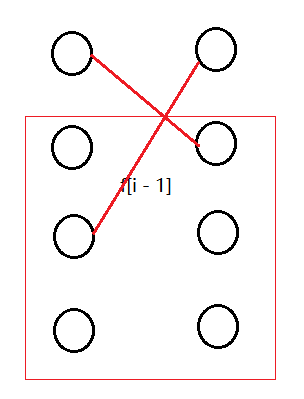
  综上：(f_i = 2 * i * f_{i - 1} - (i - 1)^2 * f_{i - 2}) 种；

• 同理：蓝色和红色一样；

• 然后容斥，解决红边和蓝边的是同一条边的情况，即至少0边是同一边的情况 - 至少 1 边是同一边 + 至少 2 边是同一边 - 至少 3 边 + ......;

• 综上：(ans = sum_{i = 0}^n(-1)^iC_n^iA_n^if_{n - i}^2)

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD = 1000000007;
const int MAXN = 10000005;
ll qpow(ll a, ll b, ll m = MOD) {
    ll ans = 1;
    for (;b;a = (a * a % m), b >>= 1)
        if (b & 1)ans = (ans * a % m);
    return ans;
}
struct CC {
    static const int N = MAXN;
    ll fac[N], inv[N];
    CC() {
        fac[0] = 1;
        for (int i = 1; i < N; ++i) fac[i] = fac[i - 1] * i % MOD;
        inv[N - 1] = qpow(fac[N - 1], MOD - 2, MOD);
        for (int i = N - 2; i >= 0; --i) inv[i] = inv[i + 1] * (i + 1) % MOD;
    }
    ll operator()(ll a, ll b) { //a>=b
        if (a < b)return 0;
        return fac[a] * inv[a - b] % MOD * inv[b] % MOD;
    }
}C;
ll f[MAXN];
inline void solve()
{
    int n; cin >> n;
    f[0] = 1, f[1] = 2;
    for (ll i = 2; i <= n; ++i)
        f[i] = (2 * i % MOD * f[i - 1] % MOD - (i - 1) * (i - 1) % MOD * f[i - 2] % MOD + MOD) % MOD;
    ll ans = 0, op, temp;
    for (ll i = 0; i <= n; ++i)
    {
        op = (i & 1) ? -1 : 1;
        temp = C(n, i) * C(n, i) % MOD * C.fac[i] % MOD * f[n - i] % MOD * f[n - i] % MOD;
        ans = ((ans + op * temp) % MOD + MOD) % MOD;
    }
    cout << ans << endl;
}
int main()
{
    int T = 1;// cin >> T;
    for (int i = 1; i <= T; ++i) solve();
    return 0;
}