带家好,今天我们来聊聊 KD-Tree(
\(k\)D-Tree,说白了就是一种能够支持在较快时间内,解决与 \(k\) 维空间内点之间最短/最远距离,或者矩形覆盖问题的数据结构,与传统的可以解决类似问题的树套树/CDQ 分治而言,KD-Tree 的好处是空间线性且能够强制在线,同时与传统的二叉搜索树类的数据结构(譬如线段树和平衡树)相同的一点是,KD-Tree 也支持打标记,这让很多矩形覆盖类问题变得容易了许多。
废话不多说,我们开始!
KD-Tree 的建立
给定 \(k\) 维空间中的 \(n\) 个点,怎样建立它们的 KD-Tree 呢?
我们考虑这样一个思想,每次随机挑选一个点 \(p_i\) 和一个坐标轴(二维平面就是 \(x\) 轴和 \(y\) 轴之一,三维空间就是 \(x,y,z\) 轴之一,以此类推),并过这个点做平行于这条坐标轴的 \(k-1\) 维超平面,这样可用将整个 \(k\) 维空间分成两部分。然后我们用选出的这个点表示整个 \(k\) 维空间,递归这个 \(k-1\) 维超平面将原 \(k\) 维空间劈成的两个子空间,然后设这个点的左右儿子分别为这两个子空间表示的节点即可。
但是显然这样复杂度会退化。因此考虑优化,显然如果我们选出了一条坐标轴,那我们肯定会贪心地选择这个坐标轴方向上那一维处于中位数的点,这样分割而成的左右两个子空间中点的个数都会除以 \(2\),KDT 的深度也就是严格的 \(\log n\) 级别的。其次,你每次选择的方向也是有讲究的,如果你每次都选择同一个方向切整个空间,那显然这样子建出来的 KD-Tree 就和你将这些点按照对应的坐标排序+线段树没啥区别。针对这个问题有两种处理方法:
- 轮换建树法,即,第一次切 \(x\) 轴,第二次切 \(y\) 轴,第三次切 \(z\) 轴,以此类推
- 最大方差法,即,每次选空间中对应维坐标方差最大的那一维。
据 cmd_blk 神仙所言,后者效率高于前者,原因未知,不过感觉实现起来也没那么复杂。求中位数可以使用 sort 排序,但也可以使用 STL 自带的 nth_element 函数,这样这一步可以做到线性,具体用法是 nth_element(l,mid,r,cmp) 表示取地址在 \([l,r]\) 位置中的元素中第 \(mid-l\) 大的元素放到 \(mid\) 地址处,顺便将比它小的元素放到 \(mid\) 左边,比它大的元素放到右边,\(\text{cmp}\) 为比较函数,用法同 sort 中的 cmp。
建树部分的代码如下:
double sqr(double x){return x*x;}
struct point{
double x[K+2];
point(){fill(x,x+K,0);}
double& operator [](int id){return x[id];}
} p[MAXN+5];
struct node{int ch[2];point val,mn,mx;} s[MAXN+5];
int ncnt=0,rt=0;
void build(int &k,int l,int r){
if(l>r) return;k=++ncnt;
static double avg[K+2],vrt[K+5];//average and variant
fill(avg,avg+K,0);fill(vrt,vrt+K,0);
for(int i=l;i<=r;i++) for(int j=0;j<K;j++) avg[j]+=p[i][j];
for(int j=0;j<K;j++) avg[j]/=(r-l+1);
for(int i=l;i<=r;i++) for(int j=0;j<K;j++) vrt[j]+=sqr(p[i][j]-avg[j]);
double mx=0;int dim=0;
for(int i=0;i<K;i++) if(vrt[i]>mx) mx=vrt[i],dim=i;
int mid=l+r>>1;
nth_element(p+l,p+mid,p+r+1,[&](point lhs,point rhs){return lhs[dim]<rhs[dim];});
build(s[k].ch[0],l,mid-1);build(s[k].ch[1],mid+1,r);
s[k].val=s[k].mn=s[k].mx=p[mid];
for(int i=0;i<K;i++){
if(s[k].ch[0]) chkmin(s[k].mn[i],s[s[k].ch[0]].mn[i]),chkmax(s[k].mx[i],s[s[k].ch[0]].mx[i]);
if(s[k].ch[1]) chkmin(s[k].mn[i],s[s[k].ch[1]].mn[i]),chkmax(s[k].mx[i],s[s[k].ch[1]].mx[i]);
}
}
其中 avg,vrt 分别表示每一维的平均值和方差,这样可以找到最大的那一维 dim 并依据 dim 维的坐标对整个空间进行划分。mn,mx 分别表示每个点对应子树中,每一维坐标的最小值/最大值,你可以理解为这个点的子树对应的子空间的范围,其具体用法后面会讲到。
值得注意的是,KD-Tree 不是 Leafy 的,即,它的非叶子节点表示一个点而不像线段树的非叶节点那样表示一段区间,因此 pushup 的方法应参照平衡树(不过貌似 cmd_blk 更喜欢写 Leafy 的 KD-Tree?)
KD-Tree 的操作
查询最近、最远点
首先你暴力一个个点枚举肯定是不行的,对于这类贡献没法拆开来的题目我们也没啥好办法直接处理,因此我们考虑一个类似于 A* 的思想,设估价函数,以查询最近点为例,我们对于每个子树设置一个估价函数 \(\text{eval_min}(k)\),具体方法将会在下面提及。然后我们考察当前节点左右儿子的估价函数,如果左边 \(<\) 右边就优先访问左边,否则优先访问右边。如果我们发现我们待访问节点的估价函数 \(>\) 答案则不进入子树,否则递归对应的子树。可以证明这样的期望复杂度 \(\log n\),最坏复杂度 \(\sqrt{n}\),但是我不会证明。
当然如果出题人比较毒瘤,还是会把你卡到 \(\sqrt{n}\) 的,这里有个比较好的应对这种问题的方法,如果我们不关心每个点的具体坐标,只关心它们的相对位置,可以考虑旋转坐标系,具体旋转方法参照我的计算几何基础。
附:各类距离/最大最小值的估价函数设置:
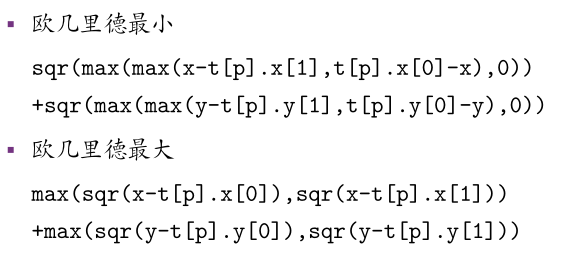

矩形查询/覆盖
按照线段树的套路从根节点开始遍历,每次遍历到一个节点,如果该节点对应的子空间完全包含于待修改/查询的空间则加上对应的贡献/打标记并返回,如果该节点对应的子空间与待修改/查询的空间没有交则直接返回,否则递归它的两个儿子。可以证明这样复杂度的上界为 \(n^{1-\frac{1}{k}}\)(这里的 \(k\) 需大于一,否则……\(\mathcal O(n)-\mathcal O(1)\) 线段树?),当 \(k=2\) 时复杂度 \(\sqrt{n}\),但我还是不会证明。
同理,如果查询矩形 \(\max\) 也可采取“如果矩形最大值小于当前答案则直接 return 的技巧”。
加入新点
对于一个给定的 KDTree 而言,如果每次往里面新添一个点,那么按照正常的插入方法复杂度最坏可达到平方,不可取。这里就有两种优化方式:
- 定期重构,如果点数达到一个阈值 \(B\) 则清空 KDT 并重新
build一遍 - 按照替罪羊树的套路,如果存在一个节点左右子树大小不平衡则重构该子树
当然由于我没有学过替罪羊树所以也没有写过支持插入的 KDTree,等学了替罪羊树再来填坑吧。
例题:
1. P6247 [SDOI2012]最近最远点对
模板题,直接建出 KDT 然后套用上面的估价函数即可。
贴一份代码:
const int MAXN=1e5;
const int K=2;
int n;
double sqr(double x){return x*x;}
struct point{
double x[K+2];
point(){fill(x,x+K,0);}
double& operator [](int id){return x[id];}
} p[MAXN+5];
double getdis(point x,point y){
double sum=0;
for(int i=0;i<K;i++) sum+=sqr(x[i]-y[i]);
return sqrt(sum);
}
struct node{int ch[2];point val,mn,mx;} s[MAXN+5];
int ncnt=0,rt=0;
void build(int &k,int l,int r){
if(l>r) return;k=++ncnt;
static double avg[K+2],vrt[K+5];//average and variant
fill(avg,avg+K,0);fill(vrt,vrt+K,0);
for(int i=l;i<=r;i++) for(int j=0;j<K;j++) avg[j]+=p[i][j];
for(int j=0;j<K;j++) avg[j]/=(r-l+1);
for(int i=l;i<=r;i++) for(int j=0;j<K;j++) vrt[j]+=sqr(p[i][j]-avg[j]);
double mx=0;int dim=0;
for(int i=0;i<K;i++) if(vrt[i]>mx) mx=vrt[i],dim=i;
int mid=l+r>>1;
nth_element(p+l,p+mid,p+r+1,[&](point lhs,point rhs){return lhs[dim]<rhs[dim];});
build(s[k].ch[0],l,mid-1);build(s[k].ch[1],mid+1,r);
s[k].val=s[k].mn=s[k].mx=p[mid];
for(int i=0;i<K;i++){
if(s[k].ch[0]) chkmin(s[k].mn[i],s[s[k].ch[0]].mn[i]),chkmax(s[k].mx[i],s[s[k].ch[0]].mx[i]);
if(s[k].ch[1]) chkmin(s[k].mn[i],s[s[k].ch[1]].mn[i]),chkmax(s[k].mx[i],s[s[k].ch[1]].mx[i]);
}
}
double mn=1e12,mx=0;
double eval_min(int k,point p){
double ret=0;
for(int i=0;i<K;i++) ret+=sqr(max(s[k].mn[i]-p[i],0.0)+max(p[i]-s[k].mx[i],0.0));
return sqrt(ret);
}
double eval_max(int k,point p){
double ret=0;
for(int i=0;i<K;i++) ret+=max(sqr(s[k].mn[i]-p[i]),sqr(p[i]-s[k].mx[i]));
return sqrt(ret);
}
void query_mn(int k,int id){
if(!k) return;
if(k!=id) chkmin(mn,getdis(s[k].val,s[id].val));
double lft=1e12,rit=1e12;
if(s[k].ch[0]) lft=eval_min(s[k].ch[0],s[id].val);
if(s[k].ch[1]) rit=eval_min(s[k].ch[1],s[id].val);
if(lft<rit){//enter left subtree first
if(lft<mn) query_mn(s[k].ch[0],id);
if(rit<mn) query_mn(s[k].ch[1],id);
} else {
if(rit<mn) query_mn(s[k].ch[1],id);
if(lft<mn) query_mn(s[k].ch[0],id);
}
}
void query_mx(int k,int id){
if(!k) return;
if(k!=id) chkmax(mx,getdis(s[k].val,s[id].val));
double lft=-1,rit=-1;
if(s[k].ch[0]) lft=eval_max(s[k].ch[0],s[id].val);
if(s[k].ch[1]) rit=eval_max(s[k].ch[1],s[id].val);
if(lft>rit){//enter left subtree first
if(lft>mx) query_mx(s[k].ch[0],id);
if(rit>mx) query_mx(s[k].ch[1],id);
} else {
if(rit>mx) query_mx(s[k].ch[1],id);
if(lft>mx) query_mx(s[k].ch[0],id);
}
}
2. P4475 巧克力王国
也是模板题,把每个巧克力看作一个二维平面直角坐标系上的一个点,然后建出 2-DT,每次在矩形内查找,如果发现矩形内所有点(方便起见,我们只需判定横纵坐标最大最小值组合而成的四个点)的 \(ax+by\) 都 \(<h\) 那就直接加上子树权值和,如果都 \(\ge h\) 就 return,否则递归左右子树。
复杂度玄学,不知道为啥能过
3. CF44G Shooting Gallery
将所有询问看作一个点建立 KDT,权值为其射击时间,将平面按照高度从小到大排序,然后按照顺序每次找到对应平面内权值最小的点,将该点对应的询问的答案设为该平面编号,然后将点权改为 \(\infty\) 即可。
时间复杂度 \(n\sqrt{m}\)
4. P2093 [国家集训队]JZPFAR
开一个小根堆存储当前距离询问点最大的 \(k\) 个点,每次遍历时发现估价函数 \(<\) 当前距离询问点最小的点的距离就 return 即可。
5. P4357 [CQOI2016]K 远点对
双倍经验
6. BZOJ #4154. [Ipsc2015]Generating Synergy
先一遍 DFS 求出所有点的 DFS 序 \(dfn_i\),然后将每个点看作一个点 \((dfn_i,dep_i)\),这样子树染色操作相当于矩形覆盖问题,直接 KDT 硬上即可。
7. P6349 [PA2011]Kangaroos
8. P6783 [Ynoi2008] rrusq
参考文献: