I. Codeforces 196C - Paint Tree(极角排序小 trick+分治)
可以考虑将以每个点为根的子树大小 (sz_i) 预处理出来。然后分治地解决这个问题。
每次分治选择当前区间中最左下角的点,然后把剩余的点按极角排序,对于树上节点 (u) 的每一个儿子 (v),为其分配长度为 (sz_v) 的一段连续区间继续递归下去。
为什么这么做法是正确的呢?我们不妨举个栗子例子看看。
假如有如下一棵树:
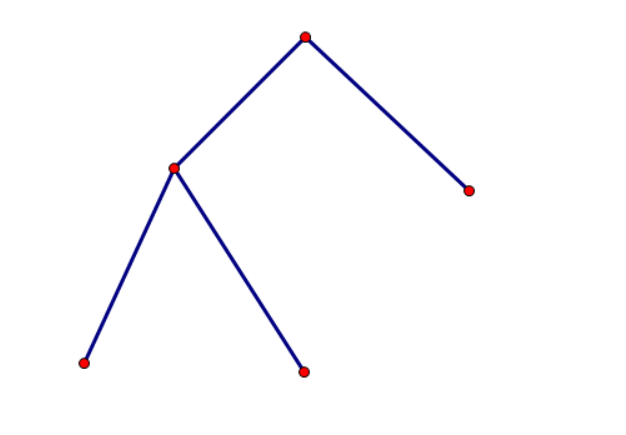
然后我们有 A,B,C,D,E 五个点需要与树上的节点一一对应:

以最左下角的 A 点为根节点,把剩余四个点按极角排序,依次为 B,C,D,E。
按照之前的推论,我们需为根节点的第一个儿子分配长度为 3 的连续区间 B,C,D(蓝色区域),为根节点的第二个儿子分配长度为 1 的连续区间 E(绿色区域)。
蓝色与绿色区域没有交集,故根节点的两棵子树中连成的线段互相之间也没有交点。
int n;
struct point{
double x,y;
int id;
} p[1505],ori;
inline bool cmp(point a,point b){
int ax=a.x-ori.x,ay=a.y-ori.y;
int bx=b.x-ori.x,by=b.y-ori.y;
return 1ll*ay*bx<=1ll*ax*by;
}
vector<int> g[1505];
int siz[1505],id[1505];
inline void findsize(int x,int f){
siz[x]=1;
foreach(it,g[x]){
int y=*it;
if(y==f) continue;
findsize(y,x);
siz[x]+=siz[y];
}
}
inline void dfs(int x,int l,int r,int f){
// cout<<x<<" "<<ind<<endl;
int o=l;
fz(i,l+1,r){
if(p[i].x<p[o].x||(p[i].x==p[o].x&&p[i].y<p[o].y)) o=i;
}
swap(p[o],p[l]);id[p[l].id]=x;ori=p[l];
sort(p+l+1,p+r+1,cmp);
// fz(i,l,r) cout<<p[i].x<<" "<<p[i].y<<" ";puts("");
int cur=l+1;
foreach(it,g[x]){
int y=*it;
if(y==f) continue;
dfs(y,cur,cur+siz[y]-1,x);
cur+=siz[y];
}
}
signed main(){
// freopen("196C.in","r",stdin);
n=read();
fz(i,1,n-1){
int u=read(),v=read();
g[u].push_back(v);
g[v].push_back(u);
}
fz(i,1,n) p[i].x=read(),p[i].y=read(),p[i].id=i;
findsize(1,0);
dfs(1,1,n,0);
fz(i,1,n) printf("%d ",id[i]);
return 0;
}
II. 洛谷 P3588 - [POI2015]PUS(线段树优化建图+拓扑排序+DP)
线段树优化建图
学完了一个 trick 当然要做几题加深一下印象咯~
首先你需要想到图论,对于每个限制你可以转化为若干条形如 ((u,v,w)) 的边表示 (a_u-a_v geq w)。
如果图中有非零环那么答案肯定为 ( exttt{NIE}),因为这样就会出现 (x>x) 的情况。
如果图中没有非零环那么原图就是一个 DAG,那么我们从入度为 (0) 的点开始进行拓扑排序。
我们设 (dp_i) 为 (a_i) 最大能达到多少,然后枚举边 ((u,v,w)),用 (dp_u-w) 来更新 (dp_v)。
如果发现存在 (a_i gt dp_i),或是存在 (dp_i leq 0),那么答案就是 ( exttt{NIE})
否则答案就是 ( exttt{TAK}),求出来的 (dp) 数组就是一个符合要求的序列。
接下来就考虑复杂度的问题,假设 (n,m,sum k) 同阶,那么暴力建边时间复杂度是 (mathcal O(nmsum k)=mathcal O(n^3)) 的,远远不够。
但是发现我们并不需要两两建边,对于每一条信息我们可以建一个“代表节点”,对于每一个 (x) 都连一条从 (x) 到这个“代表节点”,边权为 (0) 的边,然后再从这个“代表节点”向其它 (r-l+1-x) 个点连边权为 (1) 的边。不难发现这样其实与上面的建边方式是等价的。
但是这样还是会有 (nm) 条边,怎么办呢?
这时我们就要用到线段树优化建图了,将剩余 (r-l+1-x) 点拆成 (k+1) 个区间,然后套用 CF786B 的方法就可以将边数降至 (n log n) 级别了。
至此,该问题被我们解决。
你看,线段树优化建图只是一个优化建边的小 trick,这种题目归根到底还是考你图论基础与建模能力。
int n=read(),k=read(),m=read();
inline void giveup(){puts("NIE");exit(0);}
int dp[100005<<4],a[100005<<4],deg[100005<<4];
int cnt=0;
vector<pii> g[100005<<4];
bool vis[100005<<4];
inline void adde(int u,int v,int w){
g[u].push_back(pii(v,w));deg[v]++;
}
struct node{
int l,r;
} s[100005<<4];
int leaf[100005];
inline void build(int k,int l,int r){
s[k].l=l;s[k].r=r;
if(l==r){leaf[l]=k;cnt=max(cnt,k);return;}
int mid=(l+r)>>1;
adde(k,k<<1,0);adde(k,k<<1|1,0);
build(k<<1,l,mid);build(k<<1|1,mid+1,r);
}
inline void connect(int k,int l,int r,int v,int w){
if(l>r) return;
if(l<=s[k].l&&s[k].r<=r){
adde(v,k,w);
return;
}
int mid=(s[k].l+s[k].r)>>1;
if(r<=mid) connect(k<<1,l,r,v,w);
else if(l>mid) connect(k<<1|1,l,r,v,w);
else connect(k<<1,l,mid,v,w),connect(k<<1|1,mid+1,r,v,w);
}
signed main(){
build(1,1,n);
fz(i,1,100000<<3) dp[i]=1e9;
fz(i,1,k){int x=read(),y=read();dp[leaf[x]]=a[leaf[x]]=y;}
fz(i,1,m){
int l=read(),r=read(),k=read();cnt++;int pre=l;
fz(j,1,k){
int x=read();adde(leaf[x],cnt,0);
connect(1,pre,x-1,cnt,1);pre=x+1;
}
connect(1,pre,r,cnt,1);
}
queue<int> q;
fz(i,1,cnt) if(!deg[i]) q.push(i),vis[i]=1;
while(!q.empty()){
int x=q.front();q.pop();
foreach(it,g[x]){
int y=it->first,w=it->second;
deg[y]--;
if(a[y]>dp[x]-w) giveup();
dp[y]=min(dp[y],dp[x]-w);
if(dp[y]<=0) giveup();
if(deg[y]==0) q.push(y),vis[y]=1;
}
}
fz(i,1,cnt) if(!vis[i]) giveup();
puts("TAK");fz(i,1,n) printf("%d ",dp[leaf[i]]);
return 0;
}
III. Codeforces Gym 102174G - 神圣的 F2 连接着我们(最短路+线段树优化建图)
CF 上少有的中文题之一。。。。。。
第一眼:网络流?但是这数据范围提示你,这题显然不是网络流。
除了网络流,要求两点之间距离的最小值的算法还有什么?
那还用说,最短路啊!
我们在可达的点之间连边建成一张图,根据题意,答案就是 (maxlimits_{i=1}^p minlimits_{j=1}^q dis(x_i,y_j)),其中 (dis(i,j)) 表示 (i) 与 (j) 之间的距离。
但是这样肯定爆炸——建图时间复杂度爆炸,跑最短路时间复杂度同样爆炸。
那有什么好说的呢,优化呗。
使用上一题的套路,对于每一个“折跃棱镜”,新建两个代表节点 (v_1,v_2),然后枚举 (i in [a,b],j in [c,d]),建边 (i xrightarrow{w} v_1 xrightarrow{0} j),(i xleftarrow{w} v_2 xleftarrow{0} j)。
为什么是两个代表节点而不是一个代表节点?因为如果你把所有边一股脑儿连在一个节点上,那么就会存在 (c
ightarrow d),边权为 (0) 的路径,显然不符合要求啊。。。。。。
这可以进一步通过线段树优化建图优化到 (n log n) 条边。
这样建图算是优化成功了。可你跑最短路时间复杂度还会炸啊!
没关系,不难发现,后面那个 (min) 完全没有必要。因为你可以新建一个虚拟节点与 (y_1,y_2 dots y_q) 连边权为 (0) 的边,后面那个 (min) 就变为 (p_i) 到新建的那个节点的最短距离,故原问题被我们转化为一个多源单汇问题。
一不做二不休,根据我们的经验,碰到多源单汇问题,可以考虑将原图每条边都反向,源点变为汇点,汇点变为源点,然后跑一遍单源最短路径。
然后?
还有什么然后啊,跑完以后直接取一遍 (max) 不就完事儿了吗。
到这里,我们成功地把建图从 (n^3 o n^2 o n log n),跑最短路时间复杂度变为 (n^3 log n o n^2 log n o n log n),就可以在时限内通过了。
int n=read(),m=read(),p=read(),q=read();
int sx[100005],ex[100005],cnt,dist[1000005];
vector<pii> g[1000005];
inline void addedge(int x,int y,int z){
// printf("%d %d %d
",y,x,z);
g[y].push_back(pii(x,z));
}
struct node{
int l,r;
} s[100005<<2];
int leaf[100005],ncnt=0;
inline void build(int k,int l,int r){
s[k].l=l;s[k].r=r;
if(l==r){leaf[l]=k;ncnt=max(ncnt,k);return;}
int mid=(l+r)>>1;
build(k<<1,l,mid);build(k<<1|1,mid+1,r);
}
inline void connect(int k,int l,int r,int v,int w,int op){
if(l<=s[k].l&&s[k].r<=r){
if(!op) addedge(k,v,w),addedge(v+1,k,w);
else addedge(v,k+ncnt,0),addedge(k+ncnt,v+1,0);
return;
}
int mid=(s[k].l+s[k].r)>>1;
if(r<=mid) connect(k<<1,l,r,v,w,op);
else if(l>mid) connect(k<<1|1,l,r,v,w,op);
else connect(k<<1,l,mid,v,w,op),connect(k<<1|1,mid+1,r,v,w,op);
}
signed main(){
build(1,1,n);cnt=2*ncnt+2;
fz(i,2,ncnt) addedge(i,i>>1,0),addedge((i>>1)+ncnt,i+ncnt,0);
fz(i,1,m){
int a=read(),b=read(),c=read(),d=read(),w=read();
connect(1,a,b,cnt,w,0);connect(1,c,d,cnt,w,1);cnt+=2;
}
fz(i,1,p) sx[i]=read();
fz(i,1,q) ex[i]=read();
fz(i,1,q) addedge(leaf[ex[i]]+ncnt,2*ncnt+1,0);
priority_queue<pii,vector<pii>,greater<pii> > q;
fillbig(dist);dist[2*ncnt+1]=0;q.push(pii(0,2*ncnt+1));
while(!q.empty()){
pii p=q.top();q.pop();
int x=p.se,sum=p.fi;
// cout<<x<<endl;
if(dist[x]<sum) continue;
foreach(it,g[x]){
int y=it->fi,z=it->se;
if(dist[y]>sum+z){
dist[y]=sum+z;
q.push(pii(dist[y],y));
}
}
}
// fz(i,1,cnt) cout<<dist[i]<<endl;
int ans=0;
fz(i,1,p) ans=max(ans,dist[leaf[sx[i]]]);
if(ans==0x3f3f3f3f3f3f3f3fll) printf("boring game
");
else printf("%lld
",ans);
return 0;
}
IV. 洛谷 P3953 / UOJ #331 逛公园(最短路+tarjan+dp)
和 ycx 一样,一年前我写的程序被叉掉了/kk,只好重写一个。
最短路是逃不掉的,记 (1) 到各个点的最短路为 (dist_i)
首先,如果不考虑 (0) 边的情况,那么数据范围暗示我们时间复杂度为 (mathcal O(nk))。
那么就有 (dp_{u,j}) 表示走到节点 (u),经过的路径长度为 (dist_u+j) 的方案数,那么有
边界条件 (dp_{1,0}=1),最终的答案为 (sumlimits_{j=0}^kdp_{n,k})。
因为不存在 (0) 边,所以 (dp) 状态无后效性,可以采用记忆化搜索的方式实现。
接下来考虑 (0) 边的问题。显然 CCF 数据放水了,我一年前那个直接找到 (0) 环就 (-1) 的程序都可以过。
考虑以下的 hack:
5 5 0 10
1 2 0
2 3 0
3 4 0
4 2 0
1 5 1
在这个数据中,虽然存在 (0) 环 (2 o 3 o 4 o 2),可是一旦你进入 (0) 环之后就没法儿出来了!故合法路径只有一种 (1 o 5)。
因此直接 dfs 找 (0) 环的方式是错误的,我们只好另辟蹊径。
考虑对于所有零边建一个新图 (G_0)。那么对于 (G_0) 的每一个强连通分量,任意一个点都可以以 (0) 的代价到底任意另一个点。
故我们可以对 (G_0) 进行 SCC 缩点之后重新构图,为了叙述方便,我们记缩点之后每一个顶点为“大顶点”。
如果存在一个大顶点由 (x (x geq 2)) 个节点组成,并且它在 (1 o n) 的长度不超过 (dist_n+k) 的路径上,那么答案为 (-1),因为你可以从 (1) 走到这个大顶点之后在里面绕圈子,然后再走到 (n),总长不超过 (dist_n+k)。
具体怎样 check 呢?
从 (1) 开始正着跑一遍 dijkstra,建反图从 (n) 跑一遍 dijkstra(设反图上 (n) 到 (i) 的距离为 (dist'_i)),那么如果 (dist_i+dist'_i>=dist_n+k),就说明 (i) 在一条 (1 o n) 的长度不超过 (dist_n+k) 的路径上。
这样这题就被我们解决了。所以本题的难点在于如何判 (-1) 而不在于怎样计算答案。
实现起来还有不少细节要注意:
- 缩点之后,(1 o n) 的路径就变为 (from_i o from_n) 的路径。一不注意就会写成 (1) 或者 (n)。
- 本题略微有些卡常,最好使用链式前向星构图,否则有可能过不了 UOJ 的 extra test。
#define int long long
int n,m,k,mod;
struct graph{
int head[200005],nxt[200005],to[200005],c[200005],ecnt;
inline void clear(){ecnt=0;fill0(head);}
inline void adde(int u,int v,int w){
to[++ecnt]=v;c[ecnt]=w;nxt[ecnt]=head[u];head[u]=ecnt;
}
} og,g,rev,g0;
map<pii,bool> edged;
int dist_1[100005],dist_n[100005];
int dfn[100005],low[100005],stk[100005],tim=0,top=0,scc=0,vis[100005],from[100005],siz[100005];
int dp[100005][55];
inline void cleardata(){
og.clear();g.clear();g0.clear();rev.clear();
fill0(dfn);fill0(low);fill0(stk);
fill0(vis);fill0(from);fill0(siz);
tim=top=scc=0;edged.clear();
fillbig(dist_1);fillbig(dist_n);fill1(dp);
}
inline void tarjan(int x){
dfn[x]=low[x]=++tim;
stk[++top]=x;vis[x]=1;
for(int i=g0.head[x];i;i=g0.nxt[i]){
int y=g0.to[i];
if(!dfn[y]) tarjan(y),low[x]=min(low[x],low[y]);
else if(vis[y]) low[x]=min(low[x],dfn[y]);
}
if(low[x]==dfn[x]){
scc++;
while(top){
int y=stk[top--];vis[y]=0;
siz[scc]++;from[y]=scc;
if(x==y) break;
}
}
}
inline int DP(int x,int y){
if(y<0) return 0;
if(~dp[x][y]) return dp[x][y];
if(x==from[1]&&y==0) return 1;
int sum=0;
for(int i=rev.head[x];i;i=rev.nxt[i]){
int to=rev.to[i],w=rev.c[i];
sum=(sum+DP(to,y+dist_1[x]-w-dist_1[to]))%mod;
}
// cout<<x<<" "<<y<<" "<<sum<<endl;
return dp[x][y]=sum;
}
inline void solve(){
n=read();m=read();k=read();mod=read();cleardata();
fz(i,1,m){
int u=read(),v=read(),w=read();
og.adde(u,v,w);
if(!w) g0.adde(u,v,w);
}
fz(i,1,n) if(!dfn[i]) tarjan(i);
fz(i,1,n) for(int e=og.head[i];e;e=og.nxt[e]){
int j=og.to[e];
if(from[i]!=from[j]){
g.adde(from[i],from[j],og.c[e]);
// cout<<from[i]<<" "<<from[j]<<" "<<it->se<<endl;
rev.adde(from[j],from[i],og.c[e]);
}
}
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
q.push(pii(0,from[1]));dist_1[from[1]]=0;
while(!q.empty()){
pii p=q.top();q.pop();
int sum=p.fi,x=p.se;
if(dist_1[x]<sum) continue;
for(int i=g.head[x];i;i=g.nxt[i]){
int y=g.to[i],z=g.c[i];
if(dist_1[y]>sum+z){
dist_1[y]=sum+z;
q.push(pii(dist_1[y],y));
}
}
}
q.push(pii(0,from[n]));
dist_n[from[n]]=0;
while(!q.empty()){
pii p=q.top();q.pop();
int sum=p.fi,x=p.se;
if(dist_n[x]<sum) continue;
for(int i=rev.head[x];i;i=rev.nxt[i]){
int y=rev.to[i],z=rev.c[i];
if(dist_n[y]>sum+z){
dist_n[y]=sum+z;
q.push(pii(dist_n[y],y));
}
}
}
fz(i,1,scc) if(siz[i]>1&&dist_1[i]+dist_n[i]<=dist_1[from[n]]+k){
puts("-1");return;
}
int ans=0;
fz(i,0,k) ans=(ans+DP(from[n],i))%mod;
printf("%lld
",ans);
}
signed main(){
// freopen("C://Users//汤//Downloads//P3953_6.in","r",stdin);
// freopen("data.txt","w",stdout);
int T=read();
while(T--) solve();
return 0;
}
V. 洛谷 P5903 【模板】树上 k 级祖先(长链剖分模板)
就把这题当作一道长链剖分的模板题来说一下吧
长链剖分,顾名思义,就是要选取尽可能长的链。也就是把重链剖分里面“重儿子”的定义改成深度最大的点就是长链剖分了。
长链剖分有以下几条性质:
- 任意一个节点都属于恰好一条链上,这根据链剖分的定义可以直接得到,没什么好说的。
- 任意一个节点 (x) 的任意一个祖先 (y) 所在的链的长度 (geq) (x) 所在的链的长度,这也比较好理解。
- 从任意一个节点到根节点的路径上最多经过轻边的条数是 (sqrt{n}) 级别的。这个一眼看去好像没那么显然。不过你可以这么考虑:经过一条轻边,就意味着多一条链。而根据性质 (1),新的那条链的长度肯定会大于原来那条链的长度,(1,2,3,dots),最多累加到 (sqrt{n}) 级别就会超过 (n)。
长链剖分的性质就这么多。那么如何使用长链剖分的性质解决这道题呢?
显然数据范围暗示我们要 (mathcal O(log n)) 预处理,(mathcal O(1)) 查询。
倍增和重链剖分都是 (log n) 查询的,显然太逊了。
何尝不把它们结合一下呢?
我们两遍 dfs 预处理出长链剖分的一些参数。再用倍增求出每个点 (2^j) 级祖先。
然后我们干这样一件神奇的事情:将每个链的链顶 (t) 找出来,假设这条链长度为 (l),然后找出 (t) 向上 (l) 级祖先和向下 (l) 级儿子。
为什么要这么处理呢?
计 (h) 为 (k) 最大的二进制位,那么我们往上跳 (2^h) 步到达 (x'),根据性质 (2),(x') 所在链的长度 (geq 2^h >k-2^h)
我们进一步跳到 (x') 的链顶,求出剩下还需要跳的步数 (k'),显然 (k') 可正可负,也可以为 (0)。如果 (k') 为正,那我们就用向上的数组求出答案,否则用向下的数组求出答案。
这么做时间复杂度是怎样的呢?
两遍 (dfs) 是 (mathcal O(n)) 的,倍增是 (mathcal O(log n)),根据性质 (1),所有链的 (l) 之和为 (n),故处理那个向上向下的数组是 (mathcal O(n)) 的。这样查询可以做到 (mathcal O(1)),达到了我们期望的时间复杂度。
int n=read(),q=read();
unsigned int s=read();
int ecnt=0,head[500005],nxt[500005],to[500005];
inline void adde(int u,int v){
to[++ecnt]=v;nxt[ecnt]=head[u];head[u]=ecnt;
}
int fa[500005][22],mxdep[500005],dep[500005],wson[500005],top[500005];
inline void dfs1(int x){
for(int i=head[x];i;i=nxt[i]){
int y=to[i];mxdep[y]=dep[y]=dep[x]+1;dfs1(y);
if(mxdep[y]>mxdep[x]) mxdep[x]=mxdep[y],wson[x]=y;
}
}
vector<int> up[500005],down[500005];
inline void dfs2(int x,int tp){
top[x]=tp;
if(x==tp){
for(int i=0,cur=x;i<=mxdep[x]-dep[x];i++) up[x].push_back(cur),cur=fa[cur][0];
for(int i=0,cur=x;i<=mxdep[x]-dep[x];i++) down[x].push_back(cur),cur=wson[cur];
}
if(wson[x]) dfs2(wson[x],tp);
for(int i=head[x];i;i=nxt[i]){
int y=to[i];if(y!=wson[x]) dfs2(y,y);
}
}
inline unsigned int get(unsigned int x){
x^=x<<13;x^=x>>17;x^=x<<5;return s=x;
}
int ans[5000005],h[500005];
inline int query(int x,int k){
if(!k) return x;
x=fa[x][h[k]];k-=(1<<h[k]);k-=dep[x]-dep[top[x]];x=top[x];
return (k>=0)?up[x][k]:down[x][-k];
}
int rt=0;
signed main(){
fz(i,1,n) fa[i][0]=read(),((fa[i][0])?adde(fa[i][0],i):void(rt=i));
fz(i,1,20) fz(j,1,n) fa[j][i]=fa[fa[j][i-1]][i-1];
h[0]=-1;fz(i,1,n) h[i]=h[i>>1]+1;
dfs1(rt);dfs2(rt,rt);
ll anss=0;
fz(i,1,q){
int x=(ans[i-1]^get(s))%n+1;
int k=(ans[i-1]^get(s))%(dep[x]+1);
ans[i]=query(x,k);anss^=(1ll*i*ans[i]);
}
printf("%lld
",anss);
return 0;
}
VI. Codeforces 261D(树状数组+dp)
乍一看:(10^5) 的数组,要我们粘贴 (10^9) 次,得到一个 (10^{14}) 的数组,还要求 LIS?真就时间空间双重爆炸呗。
但实际上,(t) 的数据范围 (10^9) 是假的。因为假设数组 (a) 中不同数的个数为 (c),如果 (t geq c),答案就是 (c)(如果还想不明白的话,那恐怕你只能回去做做 Div2B 了)
注意到还有一个条件 (n imes maxb leq 2 imes 10^7),而 (c leq maxb),故最后粘贴得到的数组长度也不会超过 (2 imes 10^7)。
所以而已暴力枚举序列中每一个元素,使用树状数组优化,就可以了。
理论时间复杂度 (knmlog m approx 3 imes 10^9),然后还给过去了?
一言以蔽之:玄!
int k=read(),n=read(),mx=read(),t=read();
int a[100005],dp[100005],bit[100005];
inline void add(int x,int v){for(int i=x;i<=mx;i+=(i&(-i))) bit[i]=max(bit[i],v);}
inline int query(int x){int sum=0;for(int i=x;i;i-=(i&(-i))) sum=max(sum,bit[i]);return sum;}
int main(){
while(k--){
fz(i,1,n) a[i]=read();
map<int,int> mp;int sum=0;
fz(i,1,n){
if(!mp[a[i]]) mp[a[i]]++,sum++;
}
if(t>=sum){printf("%d
",sum);continue;}
fill0(dp);fill0(bit);int ans=0;
fz(i,1,t) fz(j,1,n){
int c=query(a[j]-1)+1;
if(c>dp[j]){
dp[j]=c;
ans=max(ans,c);
add(a[j],c);
}
}
printf("%d
",ans);
}
return 0;
}