hihocoder 骨牌覆盖三

 链接：http://hihocoder.com/problemset/problem/1162

#1162 : 骨牌覆盖问题·三

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

前两周里，我们讲解了2xN,3xN骨牌覆盖的问题，并且引入了两种不同的递推方法。
这一次我们再加强一次题目，对于给定的K和N，我们需要去求KxN棋盘的覆盖方案数。

提示：KxN骨牌覆盖

输入

第1行：2个整数N。表示棋盘宽度为k，长度为N。2≤K≤7，1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 12357

样例输入

2 62247088

样例输出

1399

题解：

在2xN的骨牌问题中，我们有答案的递推序列。f[n] = f[n-1]+f[n-2]。
事实上在处理3xN的问题中，也有部分选手推导出了答案的递推序列。
那么对于4xN,5xN，是否也存在答案的递推序列呢？有兴趣的选手不妨尝试推导一下。

在上一期，也就是3xN问题中，我们介绍了根据状态来递推的方法。这种方法显然是通用性最好的，可以用来解决任何K值的覆盖。
对于任意一个K值，我们每一行拥有的状态数量为2^K种。
在K=3时，我们是通过手动来枚举的8种状态之间的递推关系。
当K=4或者更大的时候，再通过手动枚举就显得不那么科学了，此时我们需要考虑如何用程序生成我们所需要的状态转移矩阵。

让我们再回头看看我们上一期提示里面放置骨牌的约定：
假设我们正在放置第i行的骨牌，那么会有下面3种方式：

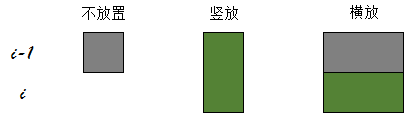
灰色表示已经有的骨牌，绿色表示新放置的骨牌。
每一种放置方法解释如下，假设当第i行的状态为x，第i-1行的状态为y：

• 第i行不放置，则前一行必须有放置的骨牌。x对应二进制位为0，y对应二进制位为1。
• 第i行竖放骨牌，则前一行必须为空。x对应二进制位为1，y对应二进制位为0。
• 第i行横向骨牌，则前一行必须两个位置均有骨牌，否则会产生空位。x对应二进制位为1，y对应二进制位为1。

通过dfs预处理就好了。接下来通过矩阵转移就可以了，复杂度为O((2^K)^3*log(L))

几个容易错的地方：状态没开够，向量矩阵未清零

转移方程 dp[i][new_state] += dp[i-1][old_state] * isright[new_state][old_state] (矩阵快速幂）

#include <bits/stdc++.h>

using namespace std;
const int maxn = 150;
const int mod = 12357;
int dp[2][maxn],L,n;
struct  Maxtri
{
    int q[maxn][maxn];
    void unit(){
        for(int i = 0; i < (1<<L); i++)
        for(int j = 0; j < (1<<L); j++)
            q[i][j] = (i == j);

    }
    int *operator[](int i){
        return q[i];
    }
    void print(){
        for(int i = 0;i<(1<<L); i++){
        for(int j=0;j<(1<<L);j++)printf("%d ",q[i][j]);
        printf("
");
        }
    }
    void init(){
        for(int i = 0; i <(1<<L); i++)
            for(int j = 0; j <(1<<L); j++)
                q[i][j] = 0;
    }

};
Maxtri w;
void dfs(int pos, int ns,int os){
    if(!pos)w[ns][os] = 1;
    else {
        if((1<<(pos-1)) & os){
            dfs(pos-1, ns, os);
            //dfs(pos-1, ns+(1<<(pos-1)), os);
            if(pos > 1)
                if((1<<(pos-2)) & os)dfs(pos-2, ns+(1<<(pos-1))+(1<<(pos-2)), os);
        }
        else dfs(pos-1, ns+(1<<(pos-1)), os);
    }
}
void init(){
    for(int i = 0; i < (1<<L); i++)
        dfs(L, 0, i);
}
Maxtri operator *(Maxtri l, Maxtri r){
    Maxtri c;
    for(int i = 0; i < (1<<L); i++)
        for(int j = 0; j <(1<<L); j++){
            c[i][j] = 0;
            for(int k = 0; k < (1<<L); k++)
                c[i][j] = (c[i][j] + l[i][k] * r[k][j]) % mod;
        }

    return c;
}
Maxtri  mul(Maxtri a ,int n){
    Maxtri rt;
    for(rt.unit(); n; n >>= 1, a=a*a)
        if(n & 1)rt = rt * a;
    return rt;
}



int main(){
    scanf("%d%d",&L,&n);

    if((n*L)%2){
        printf("%d
",0);
        return 0;
    }
    init();
    Maxtri rt =  mul(w, n);
    Maxtri vec;
    vec.init();
    vec[(1<<L)-1][0] = 1;
    int ans = 0;
    for(int i = 0; i < (1<<L); i++)
        ans = (ans + rt[(1<<L)-1][i] * vec[i][0]) % mod;
      printf("%d
",ans );
    return 0;
}

顺便说一句，今天才领会矩阵快速幂，ZYL大佬讲的真好啊