无题5

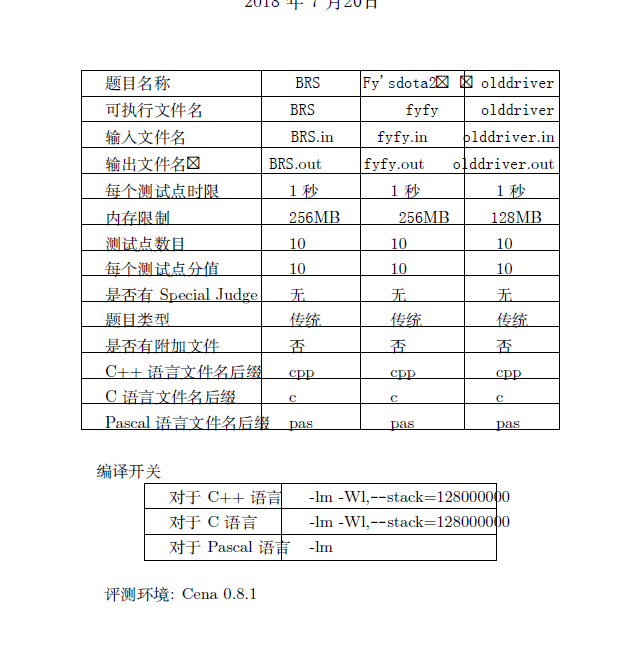
第一题：线段树求最大连续子段和，维护四个信息：区间最大子段和， 区间和， 左边最大子段和， 右边最大子段和；

查询的时候返回的是一个指针，我开始用的zero， 节约空间， 后来发现会同时有多个询问用到zero，zero会不断变化， 所以要tail++，或重新写一个up函数

#include<bits/stdc++.h>
using namespace std;


const int M = 5 * 1e5 + 10;
int n, m, inf = 2e9;
int a[M];

struct Node{
    int sum[5];
    Node *ls, *rs;
    
    void up(){
        sum[3] = ls->sum[3] + rs->sum[3];
        sum[2] = max(ls->sum[2], rs->sum[2]);
        sum[2] = max(ls->sum[1] + rs->sum[0], sum[2]);
        sum[0] = max(ls->sum[0], ls->sum[3] + rs->sum[0]);
        sum[1] = max(rs->sum[1], ls->sum[1] + rs->sum[3]);
    }
    
}pool[M << 2], *tail = pool, *root, *zero;

Node * build(int lf = 1, int rg = n){
    Node *nd = ++tail;
    if(lf == rg) {
        nd->sum[0]= nd->sum[1] = nd->sum[2] = nd->sum[3] = a[lf];
    }
    else {
        int mid = (lf + rg) >> 1;
        nd->ls = build(lf, mid);
        nd->rs = build(mid + 1, rg);
        nd->up();
    }
    return nd;
}
#define Ls lf, mid, nd -> ls
#define Rs mid+1, rg, nd -> rs
void modify(int pos, int val, int lf = 1, int rg = n, Node * nd = root){
    if(lf == rg){
        nd->sum[0]= nd->sum[1] = nd->sum[2] = nd->sum[3] = val;
    }
    else {
        int mid = (lf + rg) >> 1;
        if(pos <= mid) modify(pos, val, Ls);
        else modify(pos, val, Rs);
        nd->up();
    }
}

Node * query(int L, int R, int lf = 1, int rg = n, Node * nd = root){
    if(L <= lf && rg <= R) return nd;
    else {
        int mid = (lf + rg) >> 1;
        int t1 = 0, t2 = 0;
        if(R <= mid) return query(L, R, Ls);
        if(L > mid) return query(L, R, Rs);
        Node * a1 = query(L, R, Ls);
        Node * a2 = query(L, R, Rs);
        Node * a3 = ++tail;
        a3->ls = a1;
        a3->rs = a2;
        a3->up();
        return a3;
    }
}

int main(){
    freopen("BRS.in","r",stdin);
    freopen("BRS.out","w",stdout);
    zero = ++tail;
    zero->ls = zero->rs = zero;
    zero->sum[0] = zero->sum[1] = zero->sum[2] = zero->sum[3] = 0;
    
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)scanf("%d", &a[i]);
    root = build();
    int opt, x, y;
    while(m--){
        scanf("%d%d%d", &opt, &x, &y);
        if(opt == 1){
            Node * ans = query(x, y);
            int ret = ans->sum[2];
            printf("%d
", ret);
        }
        else modify(x, y);
    }
} 

第二题：矩阵快速幂，首先DP方程容易得：dp[s] = dp[s - 1] + dp[s - 2] + dp[s - 3] + ……+ dp[s - k];

s巨大，转移又一样，矩阵快速幂；

第一行全部赋成1， 表示dp[s] = dp[s - 1] + dp[s - 2] + dp[s - 3] + ……+ dp[s - k]; 然后每行都把原来的移过去；

转移矩阵如下：

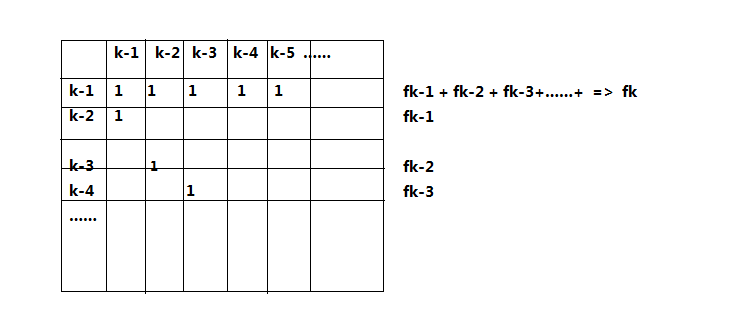
转移矩阵做 n - k 次相当于走了n-k步， 最初的矩阵就是dp数组dp[i] 再走k步就可以了；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 7777777;
int K; ll dp[15];
inline ll moc(ll a)
{
    if(a>=mod) a-=mod;
    return a;
}
struct Mat{
    ll w[15][15];
    void unit(){ 
        for(int i = 1; i <= K; i++)
            for(int j = 1; j <= K; j++)
                w[i][j] = (i == j);
    }
    
    void init(){
        for(int i = 1; i <= K; i++)
            for(int j = 1; j <= K; j++)
                w[i][j] = 0;
    }
}ori;

Mat operator * (const Mat &s, const Mat &t){
    Mat ret;
    ret.init();
    for(int i = 1; i <= K; i++)
        for(int j = 1; j <= K; j++)
            for(int k = 1; k <= K; k++)
                ret.w[i][j] = moc(ret.w[i][j] + 1ll * s.w[i][k] * t.w[k][j] % mod);
    return ret;
}
Mat ksm(Mat a, int b){
    Mat ret;
    ret.unit();
    for(; b; b >>= 1, a = a * a)
        if(b & 1) ret = ret * a;
    return ret;
}

void w(Mat a)
{
    for(int i=1;i<=K;i++)
    {
        for(int j=1;j<=K;j++)
           cout<<a.w[i][j]<<" ";
        cout<<endl;
    }
}

int main(){
    freopen("fyfy.in","r",stdin);
    freopen("fyfy.out","w",stdout);    
    int n; 
    ll ans = 0;
    scanf("%d%d", &K, &n);
    dp[0] = 1;
    for(int i = 1; i <= K; i++)
        for(int k = 0; k < i; k++)
            dp[i] = moc(dp[i] + dp[k]);
    for(int i = 1; i <= K; i++) ori.w[1][i] = 1;
    for(int i = 2; i <= K; i++) ori.w[i][i - 1] = 1;
    ori = ksm(ori, n - K);
    for(int i = 1; i <= K; i++) ans = moc(ans + ori.w[1][i] * dp[K + 1 - i] % mod);
    printf("%lld
", ans);
} 

第三题：扫描线，注意断点问题， 线段树f[o](lf -- rg) 保存的其实是y[rg] -  y[lf - 1], 不然合并的时候中间会漏掉， 所以开始的时候左区间+1； 

#include<bits/stdc++.h>
using namespace std;

const int M = 10005;
int n, q;
#define ll long long
int yy[M*2];
struct Event{
    int x, y1, y2; int d;
};
vector <Event> e;
struct Node {
    int sum;
    int cnt;
    Node *ls , *rs;
    
    void up(int l, int r){
        if(cnt) sum = yy[r] - yy[l-1];
        else if(l != r)
            sum = ls->sum + rs->sum;
        else sum = 0;
    }
}pool[M << 4], *root, *tail = pool;
Node *build(int l = 1, int r = q){
    Node * nd = ++tail;
    if(l == r)nd->sum = 0, nd->cnt = 0;
    else {
        int mid = (l + r) >> 1;
        nd->ls = build(l, mid);
        nd->rs = build(mid + 1, r);
        nd->up(l ,r);
    }
    return nd;
}
#define Ls l, mid, nd -> ls
#define Rs mid+1, r, nd -> rs
void modify(int L, int R, int d, int l = 1, int r = q, Node * nd = root){
    if(L <= l && R >= r)nd->cnt += d, nd->up(l , r);
    else {
         int mid = (l + r) >> 1;
        if(L <= mid)modify(L, R, d, Ls);
        if(R > mid)modify(L, R, d, Rs);
        nd -> up(l, r);
    }
}
bool operator < (const Event &a, const Event &b){
    return a.x < b.x;
}
int main(){
    freopen("olddriver.in","r",stdin);
    freopen("olddriver.out","w",stdout);
    scanf("%d", &n);

    int cnt = 0;
    ll ans = 0;
    for(int i = 1; i <= n; i++){
        int x1, x2, y1, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        e.push_back((Event){x1, y1, y2, 1});
        e.push_back((Event){x2, y1, y2, -1});
        yy[++cnt] = y1; yy[++cnt] = y2;
    }
    sort(yy+1, yy+1+cnt);
    sort(e.begin(), e.end());
    q = unique(yy+1, yy+1+cnt) - yy - 1;
    root = build();
    for(int i = 0; i < 2*n; i++){
        int dx = i == 0 ? 0 : e[i].x - e[i - 1].x;
        ans += 1LL*root->sum * dx;
        int p1 = find(yy+1, yy+1+q, e[i].y1) - yy;
        int p2 = find(yy+1, yy+1+q, e[i].y2) - yy;
        modify(p1+1, p2, e[i].d);
            //cout<<ans<<endl;
    }
        
    printf("%lld
", ans);
       
}