P2254 [NOI2005]瑰丽华尔兹
题目描述
不妨认为舞厅是一个N行M列的矩阵,矩阵中的某些方格上堆放了一些家具,其他的则是空地。钢琴可以在空地上滑动,但不能撞上家具或滑出舞厅,否则会损坏钢琴和家具,引来难缠的船长。每个时刻,钢琴都会随着船体倾斜的方向向相邻的方格滑动一格,相邻的方格可以是向东、向西、向南或向北的。而艾米丽可以选择施魔法或不施魔法:如果不施魔法,则钢琴会滑动;如果施魔法,则钢琴会原地不动。
艾米丽是个天使,她知道每段时间的船体的倾斜情况。她想使钢琴在舞厅里滑行的路程尽量长,这样1900 会非常高兴,同时也有利于治疗托尼的晕船。但艾米丽还太小,不会算,所以希望你能帮助她。
输入输出格式
输入格式:
输入文件的第一行包含5个数N, M, x, y和K。N和M描述舞厅的大小,x和y为钢琴的初始位置;我们对船体倾斜情况是按时间的区间来描述的,且从1开始计算时间,比如“在[1, 3]时间里向东倾斜,[4, 5]时间里向北倾斜”,因此这里的K表示区间的数目。
以下N行,每行M个字符,描述舞厅里的家具。第i 行第j 列的字符若为‘ . ’,则表示该位置是空地;若为‘ x ’,则表示有家具。
以下K行,顺序描述K个时间区间,格式为:si ti di(1 ≤ i ≤ K)。表示在时间区间[si, ti]内,船体都是向di方向倾斜的。di为1, 2, 3, 4中的一个,依次表示北、南、西、东(分别对应矩阵中的上、下、左、右)。输入保证区间是连续的,即
s1 = 1 ti = si-1 + 1 (1 < i ≤ K)
tK = T
输出格式:
输出文件仅有1行,包含一个整数,表示钢琴滑行的最长距离(即格子数)。
输入输出样例
说明
钢琴的滑行路线:
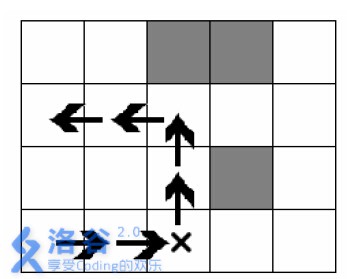
钢琴在“×”位置上时天使使用一次魔法,因此滑动总长度为6。
【数据范围】
50%的数据中,1≤N, M≤200,T≤200;
100%的数据中,1≤N, M≤200,K≤200,T≤40000。
题解:
优先队列维护二维DP,dp[i][j][k]表示i次指令后位于(j, k)的最大步数
如果在某一个点不动的最优解大于从某一个点走一些步数到他的最优解,那么之前的点是没有用的,如果遇到障碍就队列清空,四个方向,注意循环顺序。

#include<cstdio> #include<queue> #include<cstring> #include<algorithm> using namespace std; const int M = 1e6 + 10; char mp[205][205]; int q[205], f[2][205][205]; int main(){ int n, m, sx, sy, k; scanf("%d%d%d%d%d", &n, &m, &sx, &sy, &k); for(int i = 1; i <= n; i++)scanf("%s", mp[i]+1); int u = 0; memset(f[u], 0x8f, sizeof(f[u])); if(mp[sx][sy] != 'x') f[u][sx][sy] = 0; int h, t; while(k--){ int st, ed, dir; scanf("%d%d%d",&st, &ed, &dir); int len = ed - st + 1; u ^= 1; memset(f[u], 0x8f, sizeof(f[u])); switch(dir){ case 1:{ for(int j = 1; j <= m; j++){ h = 1, t = 0; for(int i = n; i; i--){ f[u][i][j] = f[u^1][i][j]; if(mp[i][j] == 'x')h = 1, t = 0; while(h <= t && f[u][i][j] > f[u^1][q[t]][j] + q[t] - i)t--; q[++t] = i; while(h <= t && q[h] - i > len)h++; if(h <= t)f[u][i][j] = max(f[u][i][j], f[u^1][q[h]][j] + q[h] - i); } } break; } case 2:{ for(int j = 1; j <= m; j++){ h = 1, t = 0; for(int i = 1; i <= n; i++){ f[u][i][j] = f[u^1][i][j]; if(mp[i][j] == 'x')h = 1, t = 0; while(h <= t && f[u][i][j] > f[u^1][q[t]][j] - q[t] + i)t--; q[++t] = i; while(h <= t && i - q[h] > len)h++; if(h <= t)f[u][i][j] = max(f[u][i][j], f[u^1][q[h]][j] - q[h] + i); } } break; } case 3:{ for(int i = n; i; i--){ h = 1, t = 0; for(int j = m; j; j--){ f[u][i][j] = f[u^1][i][j]; if(mp[i][j] == 'x')h = 1, t = 0; while(h <= t && f[u][i][j] > f[u^1][i][q[t]] + q[t] - j)t--; q[++t] = j; while(h <= t && q[h] - j > len)h++; if(h <= t)f[u][i][j] = max(f[u][i][j], f[u^1][i][q[h]] + q[h] - j); } } break; } case 4:{ for(int i = n; i; i--){ h = 1, t = 0; for(int j = 1; j <= m; j++){ f[u][i][j] = f[u^1][i][j]; if(mp[i][j] == 'x')h = 1, t = 0; while(h <= t && f[u][i][j] > f[u^1][i][q[t]] + j - q[t])t--; q[++t] = j; while(h <= t && j - q[h] > len)h++; if(h <= t)f[u][i][j] = max(f[u][i][j], f[u^1][i][q[h]] + j - q[h]); } } break; } } } int ans = 0; for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++)ans = max(ans, f[u][i][j]); printf("%d ", ans); }
