这几天上网课学了很多东西,现在整理一下
线段树
有一位老师说线段树和树状数组没有什么区别,让我们只学一个就行
我还是都学了
现在来整理一下线段树
进入正题:
在我这个线段树萌新的眼中,它就是用来求前缀和和统计的ㄟ( ▔, ▔ )ㄏ
为什么叫做线段树:
大概就是它长得很像树,然后它也是个树吧~~
至少它都有满二叉树的特点:
每个节点有一个序号 k
除了叶节点其他节点都有左孩子和右孩子
k 节点左孩子的序号为 k * 2
k 节点右孩子的序号为 k * 2 + 1
但线段树也有与众不同的特点:
存储的是一个区间的信息(如区间和)
大部分操作都是用二分的思想
便于记忆,可以直接把线段树看作是一个存储着区间信息的满二叉树
一些记忆:
以前没有学过线段树到时候,我经常把一个数组分成两部分,然后把每一段再分,一直到分成元素不能再分为止,我还经常想为什么不能这样求前缀和,不然太不方便了,结果学了线段树后发现被打脸了……
或许我早生个几十年……≖‿≖✧
线段树就是这样的:
把一个线性数组平均分成两半,然后把每一段继续分成两段,一直到只剩一个元素不能再分为止
画个图:
然后把它们当做树给编个号:

简化一下:
现在应该就能看出来了:线段树本质其实是一个满二叉树
除了叶节点,每个节点存储着一个区间的信息
而叶节点存储单个元素的信息
程序实现:
思路:
用递归分别存储一个节点的左孩子和右孩子
在存储的同时求和
建树代码:(我是从一位dalao的博客里学的)
void build_tree(int l, int r, int k) { // l 存储这个区间的左端点,r 存储这个区间的右端点,k 存储这个区间的序号
e[k].l = l;
e[k].r = r; // 用结构体存储一个节点的信息
if (l == r) { // 如果递归到一个叶节点
e[k].sum = cun[l]; // 存下这个节点的和
return; // dalao说过这句别忘了加,不然会死循环
}
int mid = (l + r) / 2; // 二分思想
build_tree(l, mid, k*2); // 递归左孩子
build_tree(mid + 1, r, k*2 + 1);// 递归右孩子
e[k].sum = e[k*2].sum + e[k*2 + 1].sum; // 求和
}
一些线段树的基本操作:
首先,先引入一个很有用的东西:延迟标记(也叫懒标记)
先举个栗子 (。・ω・)ノ゙:
有一组数:存为 a 数组,现在我要把 a[3] 到 a[7] 中间的所有数都加上 4(包括 a[3] 和 a[7]),最后输出 a[3] 到 a[7] 的区间和。
用线段树的做法怎么做?(光想思路,不用代码实现)
暴力做法:
用线段树将 a[3] 到 a[7] 的每一个点都加上 4,然后再重新求有 a[3] 到 a[7] 的所有区间的和。
有这种思路是正常的,特别是我这种蒟蒻,但这种方法实在是太暴力了,如果做题容易 TLE,因为数据一大这种方法就跟用线段树枚举没有什么区别,甚至可能比枚举的耗时还要长……
这个时候就是 超级飞侠 延迟标记发挥作用的时候了
延迟标记优化做法:
在存储树节点的结构体里再开一个变量 book
然后递归找到(下面会说做法) a[3] 到 a[7] 的区间并直接加上 4,并将 4 存储到那个区间的 book 里并把这个区间的 book 清零,下一步就是:
不管了
没错,就是不管了,反正我要求输出的是 a[3] 到 a[7] 的区间和,又没要求输出 a[3] 的值或者什么的。
那可能会有人想:
如果又要求输出 a[3] 之类的东西呢?
那这个时候就是延迟标记名字中“延迟”的由来:
如果又要求输出 a[3],那么可以再一次递归找 a[3],然后等找到 a[3] 到 a[7] 的左孩子或者右孩子的时候,由于 book 不为零,那么将这段区间的 sum 加上 book 中的值并把 book 继续下传然后清零。
画个流程:
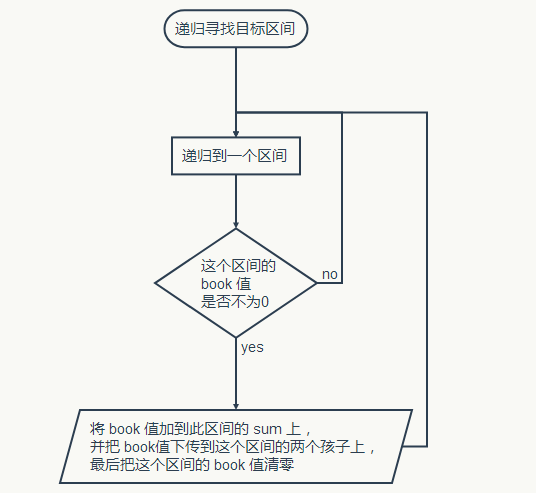
最后到达目标区间后记得 return 结束递归哦~~
流程大概就是这样,现在来解释一下:
可以这样理解:假如你的假期作业还没做(比如我),其中有要求交的,也有没让交的(老师不检查),那你会选择都做完还是只做要求教的?
反正我选二 (☆゚∀゚)
但是你现在不知道哪些作业要交,哪些作业不用交,只有课代表开始收作业的时候你才知道,那你是不是会赶紧补那个需要交的作业(争分夺秒)?
反正我会这样 (☆゚∀゚)
延迟标记就可以这样理解:如果需要这个节点的信息,那么延迟标记就赶紧把这个节点的信息给更新了,然后 光(开)荣(心)退(离)休(场)~~
就像疯狂补完该交的作业并交上去然后松了一口气的我一样(。・`ω´・)
代码实现:
void sign(int k){
e[k*2].book += e[k].book; // 将父节点的延迟标记累加到左孩子中
e[k*2 + 1].book += e[k].book; // 将父节点的延迟标记累加到右孩子中
e[k*2].sum += e[k].book * (e[k*2].r - e[k*2].l + 1); // 更新左孩子总和
e[k*2 + 1].sum += e[k].book * (e[k*2 + 1].r - e[k*2 + 1].l + 1); // 更新右孩子总和
e[k].book = 0; // 延迟标记清零
}
大约就是这个亚子
然后各操作代码:
- 单点查询:
void ask_point(int k) {
if (e[k].l == e[k].r) { // 如果查询到目标节点
ans = e[k].sum; // 记录下该节点的值
return ;
}
if (e[k].book) sign(k); // 如果这个节点的 book 值不为零,动用延迟标记
int mid = (e[k].l + e[k].r) / 2; // 二分思想
if (x <= mid) ask_point(k*2); // 如果目标节点在左区间,则递归左孩子
else ask_point(k*2 + 1);// 否则递归右孩子
}
- 单点修改:
void change_point(int k) {
if (e[k].l == e[k].r) { // 如果递归到目标节点
e[k].sum += y; // 改变该节点的值
return;
}
if (e[k].book) sign(k); // 如果这个节点的 book 值不为零,动用延迟标记
int mid = (e[k].l + e[k].r) / 2; // 二分思想
if (x <= mid) change_point(k*2); // 如果目标节点在左区间,则递归左孩子
else change_point(k*2 + 1); // 否则递归右孩子
e[k].sum = e[k*2].sum + e[k*2 + 1].sum; // 重新求和
}
- 区间查询:
void ask_line(int k) {
if (e[k].l >= a && e[k].r <= b) { // 如果递归的该区间为目标区间的一部分
ans += e[k].sum; // 累加区间和
return;
}
if (e[k].book) sign(k);
int mid = (e[k].l + e[k].r) / 2;
if (a <= mid) ask_line(k*2);
if (b > mid) ask_line(k*2 + 1);
}
- 区间修改:
void change_line(int k) {
if (e[k].l >= a && e[k].r <= b) {
e[k].sum += y * (e[k].r - e[k].l + 1);
e[k].book += y;
return;
}
if (e[k].book) sign(k);
int mid = (e[k].l + e[k].r) / 2;
if (a <= mid) change_line(k*2);
if (b > mid) change_line(k*2 + 1);
e[k].sum = e[k*2].sum + e[k*2 + 1].sum;
}
最后再次膜拜dalao
markdown真好玩
我去我竟然写了一天