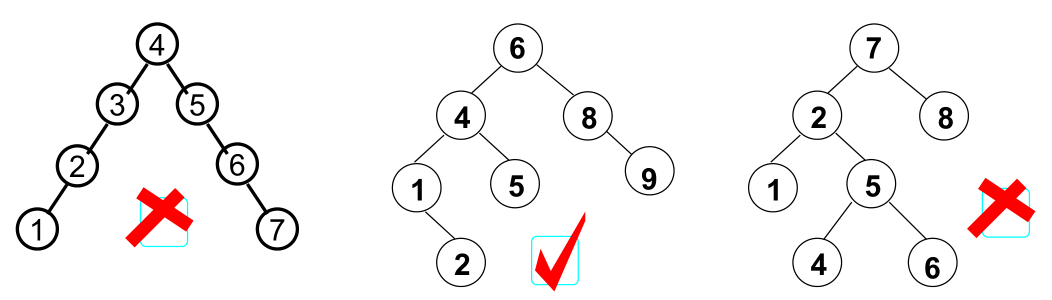
定义
平衡因子(Balance Factor ,简称BF ): BF(T) = hL -hR ,其中 hL 和 和 hR 为 分别为 T 的左、右子树的高度
平衡二叉树又称为AVL树,其定义如下:
空树,或者任一节点左右子树高度差的绝对值不超过1的二叉搜索树,即|BF(T)| ≤ 1。
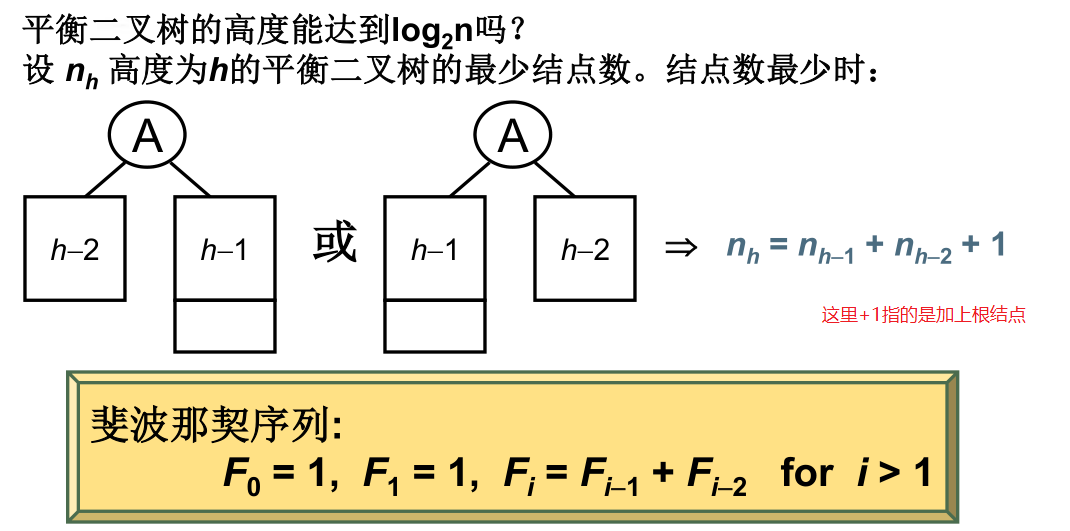

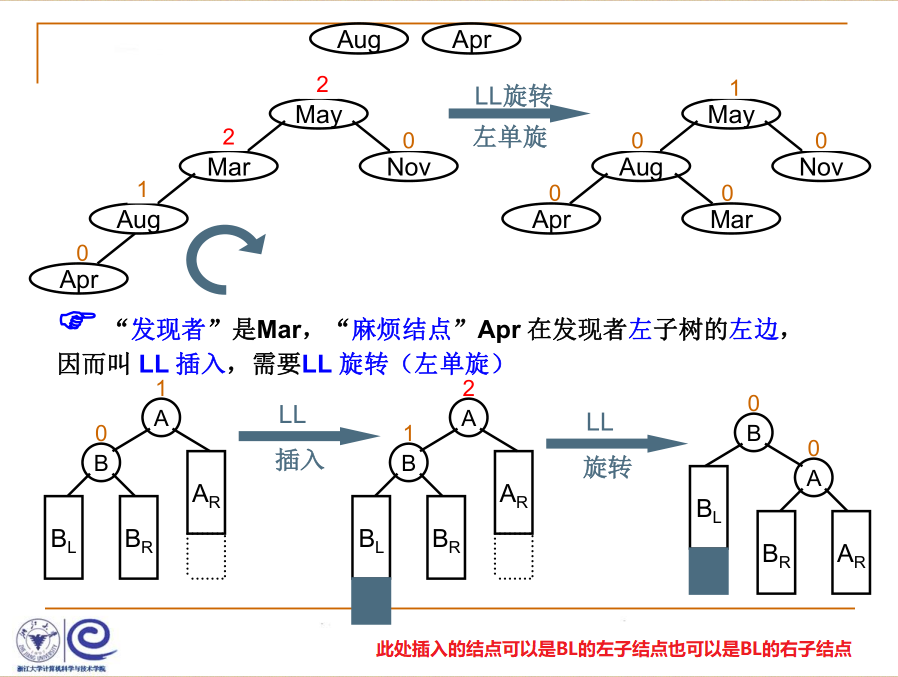
AVL树的插入(旋转)
(1) LL旋转:产生问题的结点在发现问题结点的左子树的左子树上。
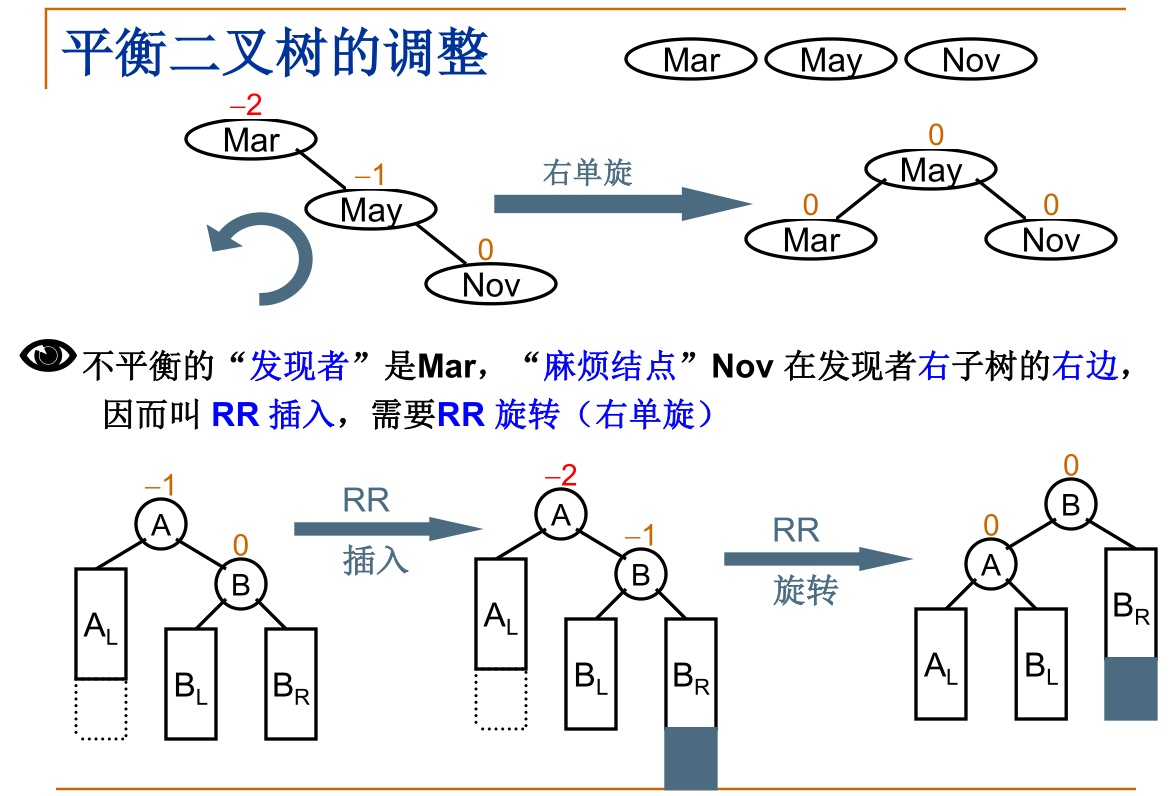
(2) RR旋转:产生问题的结点在发现问题结点的右子树的右子树上。
(3) LR旋转:产生问题的结点在发现问题结点的左子树的右子树上。
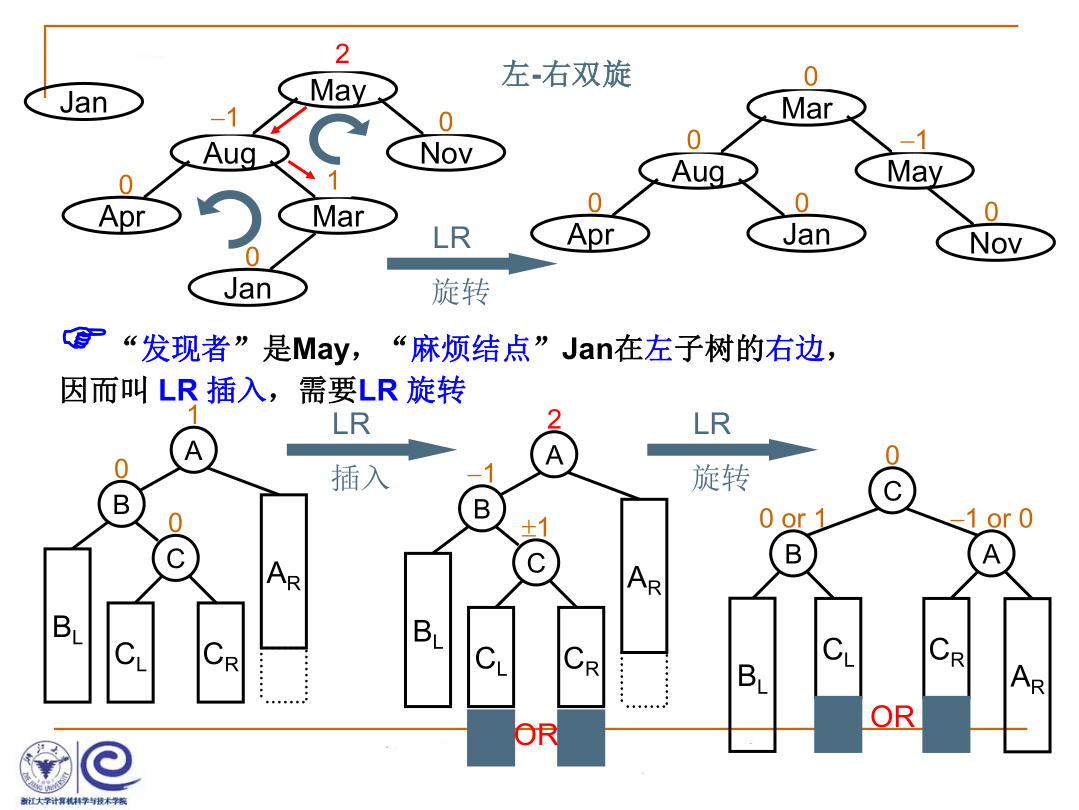
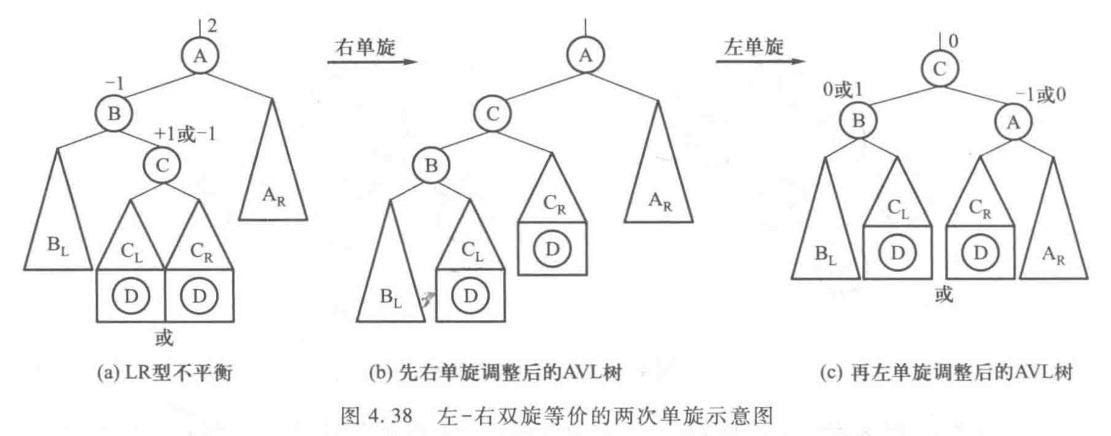
LR旋转相当于先对以B为根结点的子树做了一次右单旋(RR),再对以A为根结点的子树做了一次左单旋(LL),是两次单旋的合成结果。
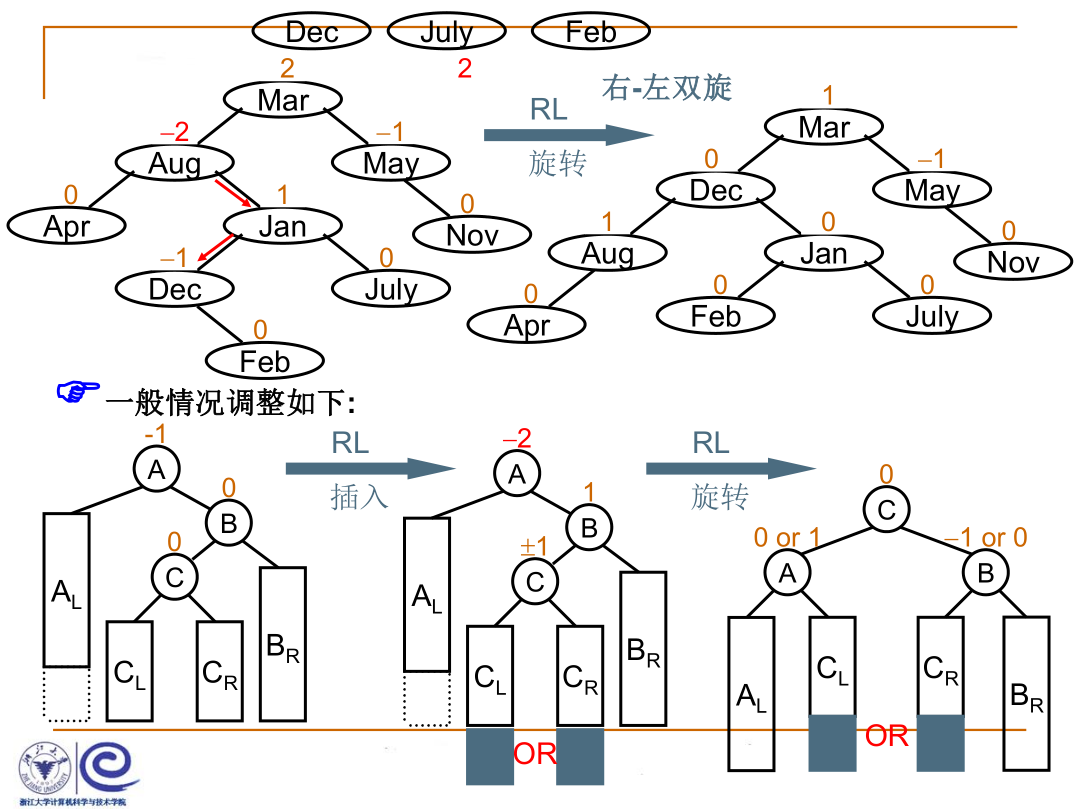
(4) RL旋转:产生问题的结点在发现问题结点的右子树的左子树上。
同理,RL旋转相当于先对以B为根结点的子树做了一次左单旋(LL),再对以A为根结点的子树做了一次右单旋(RR),是两次单旋的合成结果。
代码实现
1 typedef int ElementType; 2 typedef struct AVLNode *Position; 3 typedef Position AVLTree; /* AVL树类型 */ 4 typedef struct AVLNode 5 { 6 ElementType Data; /* 结点数据 */ 7 AVLTree Left; /* 指向左子树 */ 8 AVLTree Right; /* 指向右子树 */ 9 int Height; /* 树的高度 */ 10 }; 11 12 /* 直接获取树的高度 */ 13 int getHeight(AVLTree A) 14 { 15 if (A != NULL) 16 return A->Height; 17 else 18 return 0; 19 } 20 21 AVLTree LL(AVLTree A) 22 { 23 /* 注意:A必须有一个左子结点B */ 24 /* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */ 25 26 AVLTree B = A->Left; 27 A->Left = B->Right; 28 B->Right = A; 29 A->Height = max(getHeight(A->Left), getHeight(A->Right)) + 1; 30 B->Height = max(getHeight(B->Left), getHeight(B->Right)) + 1; 31 32 return B; /* 返回根结点 */ 33 } 34 35 AVLTree RR(AVLTree A) 36 { 37 /* 注意:A必须有一个右子结点B */ 38 /* 将A与B做右单旋,更新A与B的高度,返回新的根结点B */ 39 40 AVLTree B = A->Right; 41 A->Right = B->Left; 42 B->Left = A; 43 A->Height = max(getHeight(A->Left), getHeight(A->Right)) + 1; 44 B->Height = max(getHeight(B->Left), getHeight(B->Right)) + 1; 45 46 return B; /* 返回根结点 */ 47 } 48 49 AVLTree LR(AVLTree A) 50 { 51 /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */ 52 /* 将A、B与C做如图4.38所示的两次单旋,返回新的根结点C */ 53 54 /* 将B与C做右单旋,C被返回 */ 55 A->Left = RR(A->Left); 56 57 /* 将A与C做左单旋,C被返回 */ 58 return LL(A); 59 } 60 61 AVLTree RL(AVLTree A) 62 { 63 /* 注意:A必须有一个右子结点B,且B必须有一个左子结点C */ 64 65 /* 将B与C做左单旋,C被返回 */ 66 A->Right = LL(A->Right); 67 68 /* 将A与C做右单旋,C被返回 */ 69 return RR(A); 70 } 71 72 73 /* 将X插入AVL树T中,并且返回调整后的AVL树 */ 74 AVLTree Insert(AVLTree T, ElementType X) 75 { 76 if (T == NULL) 77 { 78 /* 若插入空树,则新建包含一个结点的树 */ 79 T = (AVLTree)malloc(sizeof(struct AVLNode)); 80 T->Data = X; 81 T->Height = 1; 82 T->Left = T->Right = NULL; 83 } 84 else if (X < T->Data) 85 { 86 /* 插入T的左子树 */ 87 T->Left = Insert(T->Left, X); 88 /* 如果需要左旋 */ 89 if (getHeight(T->Left) - getHeight(T->Right) == 2) 90 { 91 if (X < T->Left->Data) 92 T = LL(T); /* 左单旋 */ 93 else 94 T = LR(T); /* 左-右双旋 */ 95 } 96 } 97 else if (X > T->Data) 98 { 99 /* 插入T的右子树 */ 100 T->Right = Insert(T->Right, X); 101 /* 如果需要右旋 */ 102 if (getHeight(T->Left) - getHeight(T->Right) == -2) 103 { 104 if (X < T->Right->Data) 105 T = RL(T); /* 右-左双旋 */ 106 else 107 T = RR(T); /* 右单旋 */ 108 } 109 } 110 111 /* else X == T->Data,无需插入 */ 112 113 /* 别忘了更新树高 */ 114 T->Height = max(getHeight(T->Left), getHeight(T->Right)) + 1; 115 116 return T; 117 118 }
测试代码:
1 void LevelTraverse(AVLTree T) 2 { 3 if (!T) 4 return; 5 6 queue<AVLTree> Q; 7 Q.push(T); 8 while (!Q.empty()) 9 { 10 AVLTree A = Q.front(); 11 Q.pop(); 12 printf("%d ", A->Data); 13 if (A->Left) 14 Q.push(A->Left); 15 if (A->Right) 16 Q.push(A->Right); 17 } 18 } 19 20 int main() 21 { 22 AVLTree T = NULL; 23 T = Insert(T, 20); 24 T = Insert(T, 18); 25 T = Insert(T, 30); 26 T = Insert(T, 15); 27 T = Insert(T, 19); 28 T = Insert(T, 16); //破坏平衡 29 30 LevelTraverse(T); 31 32 system("pause"); 33 return 0; 34 }
参考
《 数据结构 (第2版) 》 - 陈越、何钦铭
中国大学MOOC中的浙江大学《数据结构》课程,陈越、何钦铭