一般的前馈神经网络中, 输出的结果只与当前输入有关与历史状态无关, 而递归神经网络(Recurrent Neural Network, RNN)神经元的历史输出参与下一次预测.
本文中我们将尝试使用RNN处理二进制加法问题: 两个加数作为两个序列输入, 从右向左处理加数序列.和的某一位不仅与加数的当前位有关, 还与上一位的进位有关.
词语的含义与上下文有关, 未来的状态不仅与当前相关还与历史状态相关. 因为这种性质, RNN非常适合自然语言处理和时间序列分析等任务.
RNN与前馈神经网络最大的不同在于多了一条反馈回路, 将RNN展开即可得到前馈神经网络.
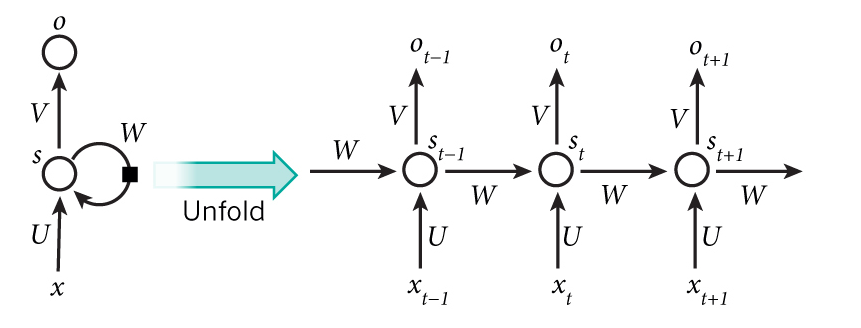
RNN同样采用BP算法进行训练, 误差反向传播时需要逆向通过反馈回路.
定义输出层误差为:
其中, (O_j)是预测输出, (T_j)是参考输出.
因为隐含层没有参考输出, 采用下一层的误差加权和代替(T_j - O_j). 对于隐含层神经元而言这里的下一层可能是输出层, 也可能是其自身.
更多关于BP算法的内容可以参考BP神经网络与Python实现
定义RNN结构
完整的代码可以在rnn.py找到.
因为篇幅原因, 相关工具函数请在完整源码中查看, 文中不再赘述.
这里我们定义一个简单的3层递归神经网络, 隐含层神经元的输出只与当前状态以及上一个状态有关.
定义RNN类:
class RNN:
def __init__(self):
self.input_n = 0
self.hidden_n = 0
self.output_n = 0
self.input_weights = [] # (input, hidden)
self.output_weights = [] # (hidden, output)
self.hidden_weights = [] # (hidden, hidden)
def setup(self, ni, nh, no):
self.input_n = ni
self.hidden_n = nh
self.output_n = no
self.input_weights = make_rand_mat(self.input_n, self.hidden_n)
self.output_weights = make_rand_mat(self.hidden_n, self.output_n)
self.hidden_weights = make_rand_mat(self.hidden_n, self.hidden_n)
这里定义了几个比较重要的矩阵:
-
input_weights: 输入层和隐含层之间的连接权值矩阵. -
output_weights: 隐含层和输出层之间的连接权值矩阵 -
hidden_weights: 隐含层反馈回路权值矩阵, 反馈回路从一个隐含层神经元出发到另一个隐含层神经元.
因为本文的RNN只有一阶反馈, 因此只需要一个反馈回路权值矩阵.对于n阶RNN来说需要n个反馈权值矩阵.
定义test()方法作为示例代码的入口:
def test(self):
self.setup(2, 16, 1)
for i in range(20000):
a_int = int(rand(0, 127))
a = int_to_bin(a_int, dim=8)
a = np.array([int(t) for t in a])
b_int = int(rand(0, 127))
b = int_to_bin(b_int, dim=8)
b = np.array([int(t) for t in b])
c_int = a_int + b_int
c = int_to_bin(c_int, dim=8)
c = np.array([int(t) for t in c])
guess, error = self.do_train([a, b], c, dim=8)
if i % 1000 == 0:
print("Predict:" + str(guess))
print("True:" + str(c))
print("Error:" + str(error))
out = 0
for index, x in enumerate(reversed(guess)):
out += x * pow(2, index)
print str(a_int) + " + " + str(b_int) + " = " + str(out)
result = str(self.predict([a, b], dim=8))
print(result)
print "==============="
do_train方法仅进行一次训练, 这里我们生成了20000组训练数据每组数据仅执行一次训练.
predict方法
predict方法执行一次前馈过程, 以给出预测输出序列.
def predict(self, case, dim=0):
guess = np.zeros(dim)
hidden_layer_history = [np.zeros(self.hidden_n)]
for i in range(dim):
x = np.array([[c[dim - i - 1] for c in case]])
hidden_layer = sigmoid(np.dot(x, self.input_weights) + np.dot(hidden_layer_history[-1], self.hidden_weights))
output_layer = sigmoid(np.dot(hidden_layer, self.output_weights))
guess[dim - i - 1] = np.round(output_layer[0][0]) # if you don't like int, change it
hidden_layer_history.append(copy.deepcopy(hidden_layer))
初始化guess向量作为预测输出, hidden_layer_history列表保存隐含层的历史值用于计算反馈的影响.
自右向左遍历序列, 对每个元素进行一次前馈.
hidden_layer = sigmoid(np.dot(x, self.input_weights) + np.dot(hidden_layer_history[-1], self.hidden_weights))
上面这行代码是前馈的核心, 隐含层的输入由两部分组成:
-
来自输入层的输入
np.dot(x, self.input_weights). -
来自上一个状态的反馈
np.dot(hidden_layer_history[-1], self.hidden_weights).
output_layer = sigmoid(np.dot(hidden_layer, self.output_weights))
guess[dim - position - 1] = np.round(output_layer[0][0])
上面这行代码执行输出层的计算, 因为二进制加法的原因这里对输出结果进行了取整.
train方法
定义train方法来控制迭代过程:
def train(self, cases, labels, dim=0, learn=0.1, limit=1000):
for i in range(limit):
for j in range(len(cases)):
case = cases[j]
label = labels[j]
self.do_train(case, label, dim=dim, learn=learn)
do_train方法实现了具体的训练逻辑:
def do_train(self, case, label, dim=0, learn=0.1):
input_updates = np.zeros_like(self.input_weights)
output_updates = np.zeros_like(self.output_weights)
hidden_updates = np.zeros_like(self.hidden_weights)
guess = np.zeros_like(label)
error = 0
output_deltas = []
hidden_layer_history = [np.zeros(self.hidden_n)]
for i in range(dim):
x = np.array([[c[dim - i - 1] for c in case]])
y = np.array([[label[dim - i - 1]]]).T
hidden_layer = sigmoid(np.dot(x, self.input_weights) + np.dot(hidden_layer_history[-1], self.hidden_weights))
output_layer = sigmoid(np.dot(hidden_layer, self.output_weights))
output_error = y - output_layer
output_deltas.append(output_error * sigmoid_derivative(output_layer))
error += np.abs(output_error[0])
guess[dim - i - 1] = np.round(output_layer[0][0])
hidden_layer_history.append(copy.deepcopy(hidden_layer))
future_hidden_layer_delta = np.zeros(self.hidden_n)
for i in range(dim):
x = np.array([[c[i] for c in case]])
hidden_layer = hidden_layer_history[-i - 1]
prev_hidden_layer = hidden_layer_history[-i - 2]
output_delta = output_deltas[-i - 1]
hidden_delta = (future_hidden_layer_delta.dot(self.hidden_weights.T) +
output_delta.dot(self.output_weights.T)) * sigmoid_derivative(hidden_layer)
output_updates += np.atleast_2d(hidden_layer).T.dot(output_delta)
hidden_updates += np.atleast_2d(prev_hidden_layer).T.dot(hidden_delta)
input_updates += x.T.dot(hidden_delta)
future_hidden_layer_delta = hidden_delta
self.input_weights += input_updates * learn
self.output_weights += output_updates * learn
self.hidden_weights += hidden_updates * learn
return guess, error
训练逻辑中两次遍历序列, 第一次遍历执行前馈过程并计算输出层误差.
第二次遍历计算隐含层误差, 下列代码是计算隐含层误差的核心:
hidden_delta = (future_hidden_layer_delta.dot(self.hidden_weights.T) +
output_delta.dot(self.output_weights.T)) * sigmoid_derivative(hidden_layer)
因为隐含层在前馈过程中参与了两次, 所以会有两层神经元反向传播误差:
- 输出层传递的误差加权和
output_delta.dot(self.output_weights.T) - 反馈回路中下一层隐含神经元传递的误差加权和
future_hidden_layer_delta.dot(self.hidden_weights.T)
将两部分误差求和然后乘自身输出的sigmoid导数sigmoid_derivative(hidden_layer)即为隐含层误差, 这里与普通前馈网络中的BP算法是一致的.
测试结果
执行test()方法可以看到测试结果:
Predict:[1 0 0 0 1 0 1 0]
True:[1 0 0 0 1 0 1 0]
123 + 15 = 138
===============
Error:[ 0.22207356]
Predict:[1 0 0 0 1 1 1 1]
True:[1 0 0 0 1 1 1 1]
72 + 71 = 143
===============
Error:[ 0.3532948]
Predict:[1 1 0 1 0 1 0 0]
True:[1 1 0 1 0 1 0 0]
118 + 94 = 212
===============
Error:[ 0.35634191]
Predict:[0 1 0 0 0 0 0 0]
True:[0 1 0 0 0 0 0 0]
41 + 23 = 64
预测精度还是很令人满意的.