LeetCode 第 211 场周赛

1624.两个相同字符之间的最长子字符串

题目链接：1624.两个相同字符之间的最长子字符串

给你一个字符串 s，请你返回 两个相同字符之间的最长子字符串的长度 ， 计算长度时不含这两个字符。如果不存在这样的子字符串，返回 -1
。

子字符串 是字符串中的一个连续字符序列。

示例 Sample

示例 1：

**输入：** s = "aa"
**输出：** 0
**解释：** 最优的子字符串是两个 'a' 之间的空子字符串。

示例 2：

**输入：** s = "abca"
**输出：** 2
**解释：** 最优的子字符串是 "bc" 。

示例 3：

**输入：** s = "cbzxy"
**输出：** -1
**解释：** s 中不存在出现出现两次的字符，所以返回 -1 。

示例 4：

**输入：** s = "cabbac"
**输出：** 4
**解释：** 最优的子字符串是 "abba" ，其他的非最优解包括 "bb" 和 "" 。

提示：

• 1 <= s.length <= 300
• s 只含小写英文字母

我的题解

class Solution {
 public:
  int maxLengthBetweenEqualCharacters(string s) {
    vector<int> c(26, -1);
    int ans(-1);
    for (int i = 0; i < s.length(); i++) {
      int ch = s[i]-'a';
      if (c[ch] != -1)
        ans = max(ans, i - c[ch]);
      else
        c[ch] = i;
    }
    return ans == -1 ? -1 : ans-1;
  }
};

1625.执行操作后字典序最小的字符串

题目链接：1625.执行操作后字典序最小的字符串

给你一个字符串 s 以及两个整数 a 和 b 。其中，字符串 s 的长度为偶数，且仅由数字 0 到 9 组成。

你可以在 s 上按任意顺序多次执行下面两个操作之一：

• 累加：将 a 加到 s 中所有下标为奇数的元素上（ 下标从 0 开始 ）。数字一旦超过 9 就会变成 0，如此循环往复。例如，s = "3456" 且 a = 5，则执行此操作后 s 变成 "3951"。
• 轮转：将 s 向右轮转 b 位。例如，s = "3456" 且 b = 1，则执行此操作后 s 变成 "6345"。

请你返回在 s 上执行上述操作任意次后可以得到的 字典序最小 的字符串。

如果两个字符串长度相同，那么字符串 a 字典序比字符串 b 小可以这样定义：在 a 和 b 出现不同的第一个位置上，字符串 a
中的字符出现在字母表中的时间早于 b 中的对应字符。例如，"0158” 字典序比 "0190" 小，因为不同的第一个位置是在第三个字符，显然
'5' 出现在 '9' 之前。

示例 Sample

示例 1：

**输入：** s = "5525", a = 9, b = 2
**输出：** "2050"
**解释：** 执行操作如下：
初态："5525"
轮转："2555"
累加："2454"
累加："2353"
轮转："5323"
累加："5222"
累加："5121"
轮转："2151"
累加："2050"​​​​​​​​​​​​
无法获得字典序小于 "2050" 的字符串。

示例 2：

**输入：** s = "74", a = 5, b = 1
**输出：** "24"
**解释：** 执行操作如下：
初态："74"
轮转："47"
累加："42"
轮转："24"​​​​​​​​​​​​
无法获得字典序小于 "24" 的字符串。

示例 3：

**输入：** s = "0011", a = 4, b = 2
**输出：** "0011"
**解释：** 无法获得字典序小于 "0011" 的字符串。

示例 4：

**输入：** s = "43987654", a = 7, b = 3
**输出：** "00553311"

提示：

• 2 <= s.length <= 100
• s.length 是偶数
• s 仅由数字 0 到 9 组成
• 1 <= a <= 9
• 1 <= b <= s.length - 1

我的题解

class Solution {
public:
    string findLexSmallestString(string s, int a, int b) {
      queue<string>que;
      set<string>vis;
      que.push(s);vis.insert(s);
      string ans(s);
      while(!que.empty()){
        string u = que.front(),v;
        ans = min(ans,u);
        que.pop();
        v = u;
        for(int i = 0 ;i < u.length();i++) if(i&1) v[i] = (u[i]-'0'+a)%10+'0';
        if(vis.find(v) == vis.end()) vis.insert(v),que.push(v);
        for(int i = 0;i < u.length();i++)
          v[(i+b)%u.length()] = u[i];
        if(vis.find(v) == vis.end()) vis.insert(v),que.push(v);
      }
      return ans;
    }
};

1626.无矛盾的最佳球队

题目链接：1626.无矛盾的最佳球队

假设你是球队的经理。对于即将到来的锦标赛，你想组合一支总体得分最高的球队。球队的得分是球队中所有球员的分数 总和 。

然而，球队中的矛盾会限制球员的发挥，所以必须选出一支 没有矛盾 的球队。如果一名年龄较小球员的分数 严格大于
一名年龄较大的球员，则存在矛盾。同龄球员之间不会发生矛盾。

给你两个列表 scores 和 ages，其中每组 scores[i] 和 ages[i] 表示第 i 名球员的分数和年龄。请你返回
所有可能的无矛盾球队中得分最高那支的分数 。

示例 Sample

示例 1：

**输入：** scores = [1,3,5,10,15], ages = [1,2,3,4,5]
**输出：** 34
**解释：** 你可以选中所有球员。

示例 2：

**输入：** scores = [4,5,6,5], ages = [2,1,2,1]
**输出：** 16
**解释：** 最佳的选择是后 3 名球员。注意，你可以选中多个同龄球员。

示例 3：

**输入：** scores = [1,2,3,5], ages = [8,9,10,1]
**输出：** 6
**解释：** 最佳的选择是前 3 名球员。

提示：

• 1 <= scores.length, ages.length <= 1000
• scores.length == ages.length
• 1 <= scores[i] <= 106
• 1 <= ages[i] <= 1000

我的题解

typedef pair<int, int> PII;

class Solution {
 public:
  int bestTeamScore(vector<int>& scores, vector<int>& ages) {
    const int n = scores.size();
    vector<PII> a(n);
    for (int i = 0; i < n; ++i) a[i].first = ages[i], a[i].second = scores[i];
    sort(a.begin(), a.end());
    vector<int> d(n, 0);
    int ans(INT_MIN);
    for (int i = 0; i < n; ++i) {
      d[i] = a[i].second;
      for (int j = 0; j < i; j++){
        if (a[i].second >= a[j].second) d[i] = max(d[i], d[j] + a[i].second);
      }
      ans = max(ans, d[i]);
    }
    return ans;
  }
};

1627.带阈值的图连通性

题目链接：1627.带阈值的图连通性

有 n 座城市，编号从 1 到 n 。编号为 x 和 y 的两座城市直接连通的前提是： x 和 y 的公因数中，至少有一个
严格大于 某个阈值 threshold 。更正式地说，如果存在整数 z ，且满足以下所有条件，则编号 x 和 y
的城市之间有一条道路：

• x % z == 0
• y % z == 0
• z > threshold

给你两个整数 n 和 threshold ，以及一个待查询数组，请你判断每个查询 queries[i] = [ai, bi] 指向的城市
ai 和 bi 是否连通（即，它们之间是否存在一条路径）。

返回数组 answer ，其中answer.length == queries.length 。如果第 i 个查询中指向的城市 ai 和
bi 连通，则 answer[i] 为 true ；如果不连通，则 answer[i] 为 false 。

示例 Sample

示例 1：

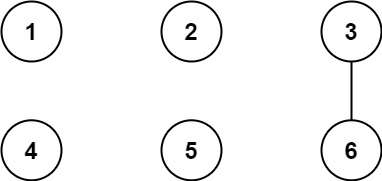
**输入：** n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
**输出：** [false,false,true]
**解释：** 每个数的因数如下：
1:   1
2:   1, 2
3:   1, **3**
4:   1, 2, **4**
5:   1, **5**
6:   1, 2, **3** , **6**
所有大于阈值的的因数已经加粗标识，只有城市 3 和 6 共享公约数 3 ，因此结果是：
[1,4]   1 与 4 不连通
[2,5]   2 与 5 不连通
[3,6]   3 与 6 连通，存在路径 3--6

示例 2：

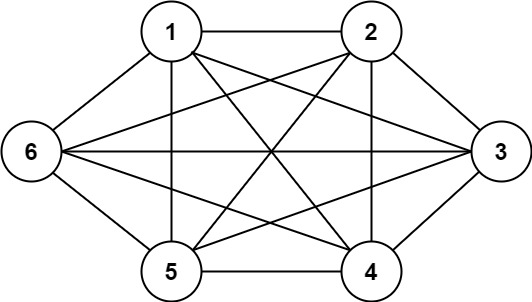
**输入：** n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]
**输出：** [true,true,true,true,true]
**解释：** 每个数的因数与上一个例子相同。但是，由于阈值为 0 ，所有的因数都大于阈值。因为所有的数字共享公因数 1 ，所以所有的城市都互相连通。

示例 3：

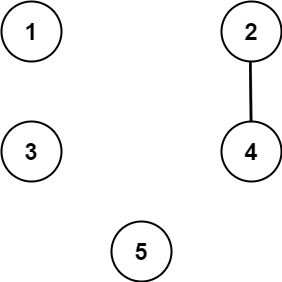
**输入：** n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]
**输出：** [false,false,false,false,false]
**解释：** 只有城市 2 和 4 共享的公约数 2 严格大于阈值 1 ，所以只有这两座城市是连通的。
注意，同一对节点 [x, y] 可以有多个查询，并且查询 [x，y] 等同于查询 [y，x] 。

提示：

• 2 <= n <= 104
• 0 <= threshold <= n
• 1 <= queries.length <= 105
• queries[i].length == 2
• 1 <= ai, bi <= cities
• ai != bi

我的题解

class Solution {
 public:
  int get_f(vector<int>& f, int v) const { return f[v] = f[v] == v ? v : get_f(f, f[v]); }

  vector<bool> areConnected(int n, int threshold, vector<vector<int>>& queries) {
    vector<int>f(n+1);
    for (int i = 0; i <= n; ++i) f[i] = i;
    for (int i = threshold + 1; i <= n; i++) {
      for (int j = i; j <= n; j += i) {
        int u = i, v = j;
        u = get_f(f, u), v = get_f(f,v);
        f[u] = v;
      }
    }
    const int m = queries.size();
    vector<bool> ans(m);
    for (int i = 0; i < m; i++) {
      int u = queries[i][0], v = queries[i][1];
      ans[i] = get_f(f, u) == get_f(f, v);
    }
    return ans;
  }
};