2019icpc南昌邀请赛F（线段树）

题目链接：https://nanti.jisuanke.com/t/40258

题意：给长为n的数组a，有m次操作，包括单点修改和查询F(l,r)，其值为所有f(i,j)的异或和，l<=i<=j<=r，即

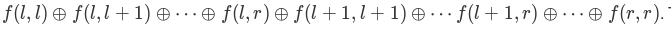
其中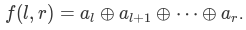

(n,m<=1e5).

思路：这种题可以用线段树来进行修改和查询，但需要先化简。对于l<=x<=r，包括ax的区间有(r-x+1)*(x-l+1)个，注意到当区间长为偶数时，改值恒为偶数，那么也就是说ax出现偶数次，那么查询结果为0。当区间长度为奇数时，若x与l奇偶性不同，则该值为偶数，异或值为0; 若奇偶值相同，则该值为奇数，异或值为ax，故需要用线段树维护与l奇偶性相同的元素的异或和。

　　　但是合并两个区间的时候，可能出现右区间的l与左区间的l奇偶性不同的情况，这时，右区间维护的值不能直接求与。需要同右区间整体异或和异或之后得到与左区间的l奇偶性相同的那些元素的异或和。说的很绕，手动算一下就明白，所以我们还需要用线段树维护区间的异或和。

AC代码：

#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn=100005;

int T,n,m,cas,a[maxn];

struct node{
    int l,r;
    int sum,val;
}tr[maxn<<2];

void pushup(int v){
    tr[v].sum=tr[v<<1].sum^tr[v<<1|1].sum;
    if((tr[v<<1|1].l-tr[v].l)%2==0)
        tr[v].val=tr[v<<1].val^tr[v<<1|1].val;
    else
        tr[v].val=tr[v<<1].val^(tr[v<<1|1].sum^tr[v<<1|1].val);
}

void build(int v,int l,int r){
    tr[v].l=l,tr[v].r=r;
    if(l==r){
        tr[v].sum=tr[v].val=a[l];
        return;
    }
    int mid=(l+r)>>1;
    build(v<<1,l,mid);
    build(v<<1|1,mid+1,r);
    pushup(v);
}

void update(int v,int x,int y){
    if(tr[v].l==tr[v].r){
        tr[v].sum=tr[v].val=y;
        return;
    }
    int mid=(tr[v].l+tr[v].r)>>1;
    if(x<=mid) update(v<<1,x,y);
    else update(v<<1|1,x,y);
    pushup(v);
}

void query(int v,int l,int r,int& x,int& y){
    if(tr[v].l==l&&tr[v].r==r){
        x=tr[v].val;
        y=tr[v].sum;
        return;
    }    
    int mid=(tr[v].l+tr[v].r)>>1;
    if(r<=mid)
        query(v<<1,l,r,x,y);
    else if(l>mid)
        query(v<<1|1,l,r,x,y);
    else{
        int a,b,c,d;
        query(v<<1,l,mid,a,b);
        query(v<<1|1,mid+1,r,c,d);
        if((tr[v<<1|1].l-l)%2==0)
            x=a^c,y=b^d;
        else
            x=a^(d^c),y=b^d;
    }
}

int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;++i)
            scanf("%d",&a[i]);
        build(1,1,n);
        printf("Case #%d:
",++cas);
        while(m--){
            int op,x,y;
            scanf("%d%d%d",&op,&x,&y);
            if(op==0)
                update(1,x,y);
            else{
                if((y-x+1)%2==0)
                    printf("0
");
                else{
                    int a,b;
                    query(1,x,y,a,b);
                    printf("%d
",a);
                }
            }
        }
    }
    return 0;
}