2019icpc南昌邀请赛B Polynomial （拉格朗日插值法）

题目链接：https://nanti.jisuanke.com/t/40254

题意：

思路：

这题要用到拉格朗日插值法，网上查了一下，找到一份讲得特别好的：

--------------------------------------------------------

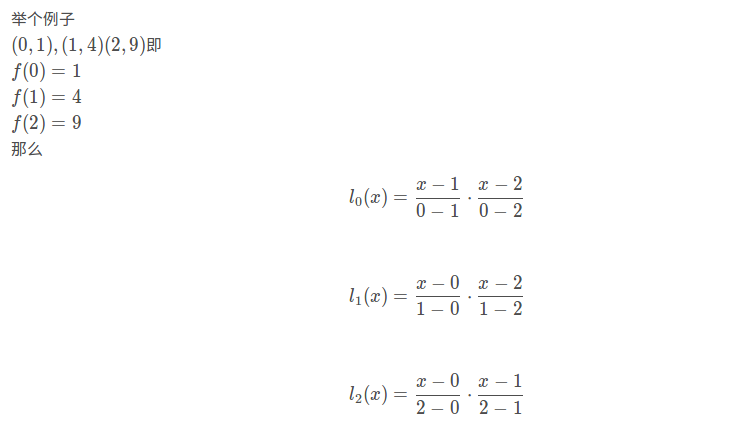
以上关于拉格朗日插值法的理论转载自：https://blog.csdn.net/ftx456789/article/details/90750508

关于这道题的做法：
这题给了x从0~n的n+1种取值，那么可以用O(n)来插值，但是它所要求的是。能够想到要用前缀来预处理，我们令：

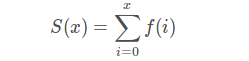，则答案为。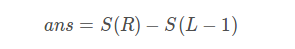

直接预处理S(x)肯定会T，我们再用一次拉格朗日插值法。

先知道一个常识：n次多项式的前缀和是 n+1 次的多项式，也就是说 S(x)S(x) 要通过 n+2 个点来求出，然而题目只给出了n+1 个点。我们利用前面的插值法求出f(n+1)，这样就有了n+2个点。之后就可以对S(x) 进行插值了。总复杂度为O(T*m*n)

要注意的是要线性求逆元，如果用费马小定理会T。

AC代码：

#include<cstdio>
#include<algorithm>
using namespace std;

typedef long long LL;

const int maxn=1005;
const int MOD=9999991;

int T,n,m;
LL a[maxn],inv[MOD+5],finv[maxn];
LL sum[maxn],ans;

LL qpow(LL a,LL b){
    LL res=1;
    while(b){
        if(b&1) res=res*a%MOD;
        a=a*a%MOD;
        b>>=1;
    }
    return res;
}

void init(){
    inv[1]=1;
    for(int i=2;i<=MOD+5;++i)
        inv[i]=(MOD-MOD/i)*inv[MOD%i]%MOD;
    finv[0]=1;
    for(int i=1;i<=1000;++i)
        finv[i]=finv[i-1]*inv[i]%MOD;
}

LL cal(LL x,LL *a,LL up){
    LL res=0;
    LL p=1;
    for(LL i=0;i<=up;++i)
        p=p*(x-i)%MOD;
    for(LL i=0;i<=up;++i){
        int f=(up-i)&1?-1:1;
        res=(res+MOD+a[i]*f*p%MOD*inv[x-i]%MOD*finv[i]%MOD*finv[up-i]%MOD)%MOD;
    }
    return res;
}

int main(){
    init();
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m);
        for(int i=0;i<=n;++i){
            scanf("%lld",&a[i]);
            a[i]%=MOD;
        }
        a[n+1]=cal(n+1,a,n);
        sum[0]=a[0];
        for(int i=1;i<=n+1;++i)
            sum[i]=(sum[i-1]+a[i])%MOD;
        while(m--){
            int l,r;
            scanf("%d%d",&l,&r);
            if(r<=n+1){
                printf("%lld
",(sum[r]-sum[l-1]+MOD)%MOD);
                continue;
            }
            if(l-1<=n+1)
                ans=(cal(r,sum,n+1)-sum[l-1]+MOD)%MOD;
            else
                ans=(cal(r,sum,n+1)-cal(l-1,sum,n+1)+MOD)%MOD;
            printf("%lld
",ans);
        }
    }
    return 0;
}