【Luogu P4071】[SDOI2016]排列计数

题目大意：

求有多少种 (1) 到 (n) 的排列 (a)，满足序列恰好有 (m) 个位置 (i)，使得 (a_i=i)，答案对 (10^{9}+7)。

正文：

可以先列个表：

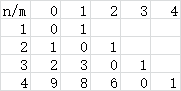
再从题目意思出发，若 (m=0)，即没有一个数字在自己位置上，那就是错位排列。错位排列的递推式是 (f_i=(i-1)(f_{i-1}+f{i-2}))。而我们在列表的过程中会发现，特殊情况除外，除在自己位置上的 (m) 个数，其它的数进行错位排列。也就是说 最终答案 = 确定排列的数的总值 * 其它数错位排列。

问题来了，确定排列的数的总值是多少？我们不妨举举例，设 (n=4,m=2)，那么就有 ({1,2,x,x},{1,x,3,x},{1,x,x,4},{x,2,3,x},{x,2,x,4},{x,x,3,4}).总共就有 (C_{n}^{m})

代码：

ll _pow(ll a, int b){
    a %= p;
	ll ans = 1;
	for(; b; b >>= 1, a = a * a % p)
		if(b & 1)
			ans = ans * a % p;
    return ans;
}
void init()
{
	prod[0] = 1;
	for (register int i = 1; i <= 1000000; i++)
		prod[i] = (prod[i - 1] * i) % p,
		inv[i] = _pow(prod[i], p - 2);
	a[2] = 1;
	for (register int i = 3; i <= 1000000; i++)
		a[i] = (i - 1) * ((a[i - 1] + a[i - 2]) % p) % p;
}

int main()
{
	int t;
	init();
	for (scanf("%d", &t); t--;)
	{
		scanf("%d%d", &n, &m);
		if(m == 0)
		{
			printf("%lld
", a[n]);
			continue;
		}
		if(n == m){puts("1");continue;}
		if(n - 1 == m){puts("0");continue;}  //图表中的几个特殊情况
		printf("%lld
", (prod[n] * inv[m] % p * inv[n-m] % p) * a[n-m] % p); //括号内的是组合数，a数组是错位排列个数
	}
	return 0;
}