题目大意:
现在给出一个仙人掌图(即每条边最多只出现在一个环里),给出多个询问,每个询问求出两点的最短距离。
正文:
概述:
仙人掌是图,由于时空限制,直接求多源最短路径会超时超空,所以我们通过 圆方树 来将其转化为树上问题。
圆方树:
关于圆方树,要讲得通俗易懂,原图里每个节点都是原点,将每个环里加入一个方点,方点直接连向环内各个节点,如图:
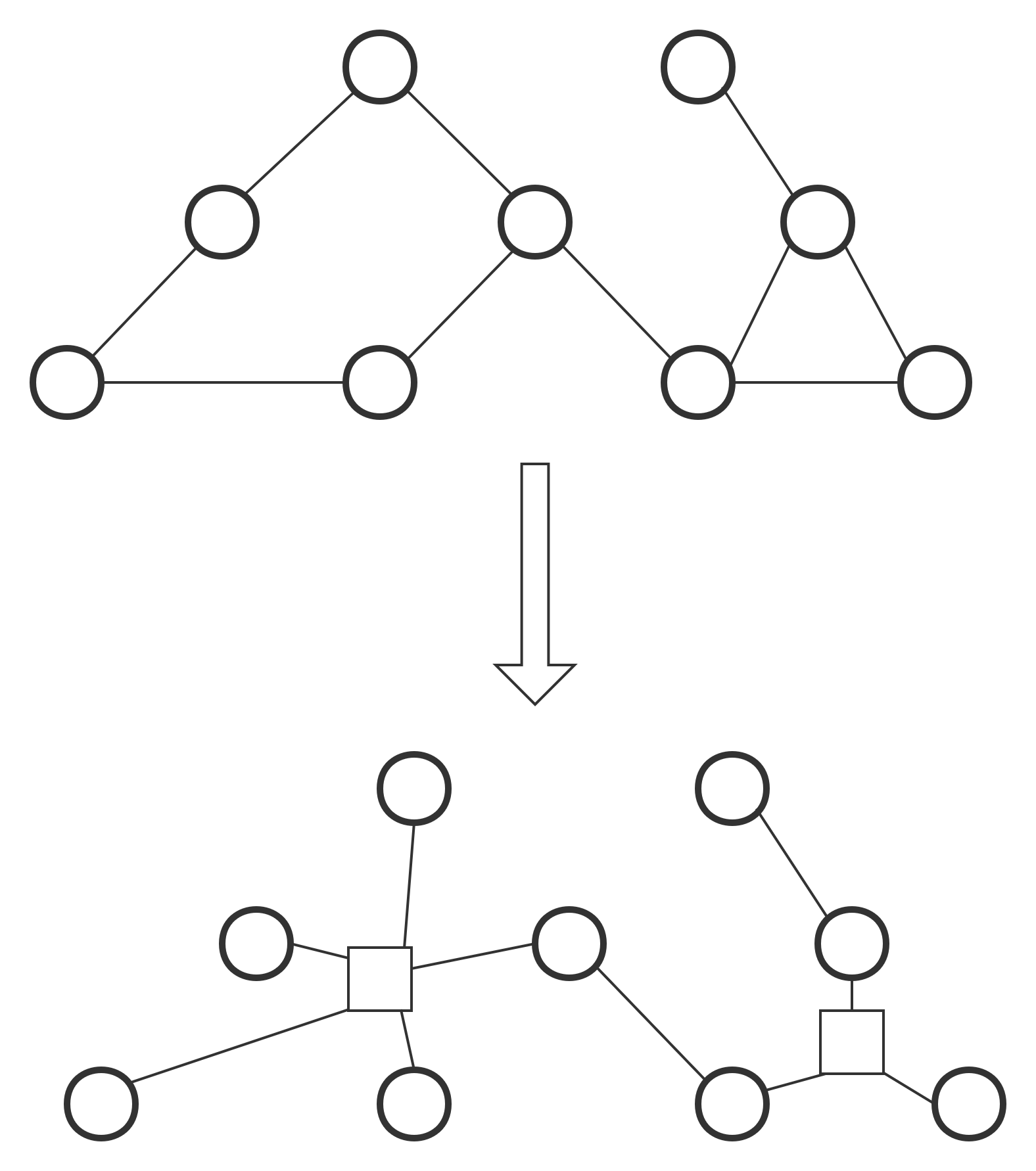
这个建方点的操作用 Tarjan 做就行了!
inline void solve (int u, int v, int w) //建方点
{
++ext;
int minn, pre = w, i = v;
while (i != f[u][0])
{
sum[i] = pre;
pre += b[i];
i = f[i][0];
}
sum[ext] = sum[u];
sum[u] = 0;
i = v;
while(i != f[u][0])
{
minn = min(sum[i], sum[ext] - sum[i]);
add_(ext, i, minn);
add_(i, ext, minn);
i = f[i][0];
}
}
void Tarjan(int u, int fa)
{
dfn[u] = low[u] = ++cnt;
for (int i = head[u]; i; i = e[i].next) //Tarjan 模板
{
int v = e[i].to, w = e[i].w;
if(v == fa) continue;
if(!dfn[v])
{
f[v][0] = u;
b[v] = w;
dis[v] = dis[u] + w;
Tarjan(v, u);
low[u] = min(low[u], low[v]);
}
else low[u] = min(low[u], dfn[v]);
if(low[v] <= dfn[u]) continue; // 建圆点
add_(u, v, w);
add_(v, u, w);
}
for (int i = head[u]; i; i = e[i].next) //找到非树边(环),建方点
{
int v = e[i].to;
if(f[v][0] == u || dfn[v] <= dfn[u]) continue;
solve(u, v, e[i].w);
}
}
对于剩下的问题——两点距离,先找到 (u,v) 的最近公共祖先 (a),(a) 是圆点直接求。如果是方点:
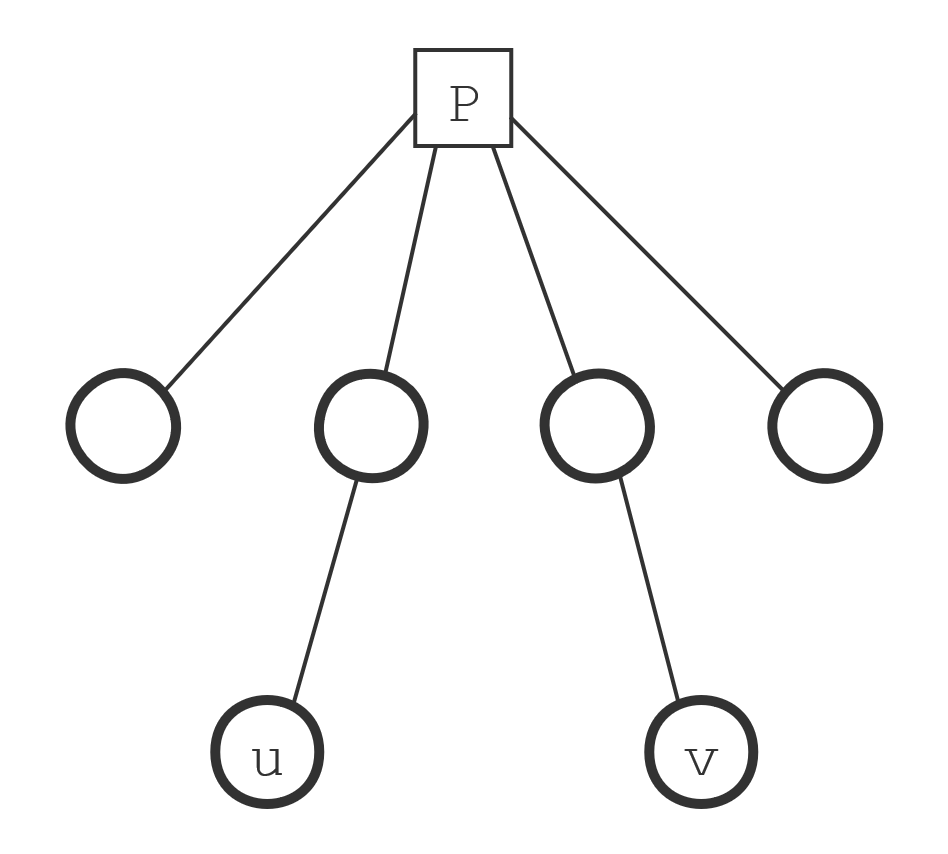
假设 (u,v) 父亲分别是 (A,B),发现如果是方点,答案就是 (operatorname{dis}(A,B)+operatorname{dis}(u,A)+operatorname{dis}(v,B))。
ll lca (int X, int Y)
{
int Lca, x = X, y = Y;
if (d[x] > d[y])
{
int t = x;
x = y;
y = t;
}
for (int i = 20; i >= 0; i--)
if (d[f[y][i]] >= d[x])
y = f[y][i];
if (x == y) Lca = x;
else
{
for (int i = 20; i >= 0; i--)
if (f[x][i] != f[y][i])
{
x = f[x][i];
y = f[y][i];
}
Lca = f[y][0];
}
ll calc = dis[X] + dis[Y] - (dis[Lca] << 1);
if(Lca > n)
{
calc -= (dis[x] - dis[Lca]) + (dis[y] - dis[Lca]);
calc += min(abs(sum[y] - sum[x]), sum[Lca] - abs(sum[y] - sum[x]));
}
return calc;
}
全部代码:
初始图和圆方树记得分着存。
struct edge
{
int from, to, next, w;
}e[M], ne[M];
int head[N], h[N], tot, total;
void add(int u, int v, int w)
{
e[++tot] = (edge){u, v, head[u], w}, head[u] = tot;
}
void add_(int u, int v, int w)
{
ne[++total] = (edge){u, v, h[u], w}, h[u] = total;
}
int dfn[N], low[N], f[N][22], cnt, d[N], b[N]; //b[u]表示u到父节点的价值
ll dis[N], sum[N];
inline void solve (int u, int v, int w) //建方点
{
++ext;
int minn, pre = w, i = v;
while (i != f[u][0])
{
sum[i] = pre;
pre += b[i];
i = f[i][0];
}
sum[ext] = sum[u];
sum[u] = 0;
i = v;
while(i != f[u][0])
{
minn = min(sum[i], sum[ext] - sum[i]);
add_(ext, i, minn);
add_(i, ext, minn);
i = f[i][0];
}
}
void Tarjan(int u, int fa)
{
dfn[u] = low[u] = ++cnt;
for (int i = head[u]; i; i = e[i].next) //Tarjan 模板
{
int v = e[i].to, w = e[i].w;
if(v == fa) continue;
if(!dfn[v])
{
f[v][0] = u;
b[v] = w;
dis[v] = dis[u] + w;
Tarjan(v, u);
low[u] = min(low[u], low[v]);
}
else low[u] = min(low[u], dfn[v]);
if(low[v] <= dfn[u]) continue; // 建圆点
add_(u, v, w);
add_(v, u, w);
}
for (int i = head[u]; i; i = e[i].next) //找到非树边(环),建方点
{
int v = e[i].to;
if(f[v][0] == u || dfn[v] <= dfn[u]) continue;
solve(u, v, e[i].w);
}
}
queue<int> que;
void dfs (int x, int fa)
{
d[x] = d[fa] + 1;
f[x][0] = fa;
for (int i = h[x]; i; i = ne[i].next)
{
int y = ne[i].to;
if(y == fa) continue;
dis[y] = dis[x] + ne[i].w;
dfs (y, x);
}
}
ll lca (int X, int Y)
{
int Lca, x = X, y = Y;
if (d[x] > d[y])
{
int t = x;
x = y;
y = t;
}
for (int i = 20; i >= 0; i--)
if (d[f[y][i]] >= d[x])
y = f[y][i];
if (x == y) Lca = x;
else
{
for (int i = 20; i >= 0; i--)
if (f[x][i] != f[y][i])
{
x = f[x][i];
y = f[y][i];
}
Lca = f[y][0];
}
ll calc = dis[X] + dis[Y] - (dis[Lca] << 1);
if(Lca > n)
{
calc -= (dis[x] - dis[Lca]) + (dis[y] - dis[Lca]);
calc += min(abs(sum[y] - sum[x]), sum[Lca] - abs(sum[y] - sum[x]));
}
return calc;
}
int main()
{
scanf ("%d%d", &n, &m);
ext = n;
for (int i = 1; i <= m; ++i)
{
int u, v, w;
scanf ("%d%d%d", &u, &v, &w);
add(u, v, w);
add(v, u, w);
}
f[1][0] = 0;
Tarjan(1, 0);
for (int i = 1; i <= ext; i++)
d[i] = 0, dis[i] = 0;
dfs(1, 0);
for (int j = 1; j <= 20; j++)
for (int i = 1; i <= ext; i++)
f[i][j] = f[f[i][j - 1]][j - 1];
scanf ("%d", &q);
for (int i = 1; i <= q; ++i)
{
int x, y;
scanf ("%d%d", &x, &y);
printf("%lld
", lca(x, y));
}
return 0;
}