原文地址:http://www.cnblogs.com/GXZlegend/p/6812435.html
题目描述
Pine开始了从S地到T地的征途。
从S地到T地的路可以划分成n段,相邻两段路的分界点设有休息站。
Pine计划用m天到达T地。除第m天外,每一天晚上Pine都必须在休息站过夜。所以,一段路必须在同一天中走完。
Pine希望每一天走的路长度尽可能相近,所以他希望每一天走的路的长度的方差尽可能小。
帮助Pine求出最小方差是多少。
设方差是v,可以证明,v×m^2是一个整数。为了避免精度误差,输出结果时输出v×m^2。
输入
第一行两个数 n、m。
第二行 n 个数,表示 n 段路的长度
输出
一个数,最小方差乘以 m^2 后的值
样例输入
5 2
1 2 5 8 6
样例输出
36
题解
斜率优化(不需要二维)
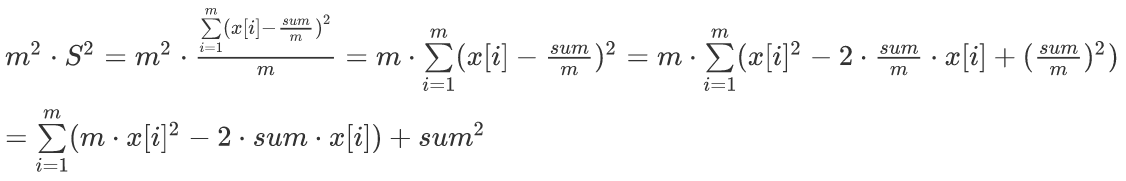
所以只要维护∑m*x[i^2-2*sum*x[i]的最小值即可。
设f[i][j]为前i条路分为j段的∑最小值,那么显然有f[i][j]=f[k][j-1]+m*(sum[i]-sum[k])*(sum[i]-sum[k])-2*sum[n]*(sum[i]-sum[k])。
这样dp时间复杂度为O(n^2*m),会TLE,需要优化。
将上述dp方程平方展开并移项,得到f[k][j-1]+m*sum[j]^2+2*sum[n]*sum[j]=2*m*sum[i]*sum[j]+f[i][j]-m*sum[i]^2+2*sum[n]*sum[i]
这样可以用斜率优化来优化。
由于第二维j的存在,需要先循环第二维j,再循环第一维i,并将每次的f[i][j-1]与队列中元素比较并插入。
代码中可以看到我开了滚动数组,但好像没什么必要,直接开二维就行。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 3010
#define y(i , p) (f[i][p] + m * sum[i] * sum[i] + 2 * sum[n] * sum[i])
using namespace std;
typedef long long ll;
int q[N];
ll a[N] , sum[N] , f[N][2];
int main()
{
int n , m , i , j , l , r , d;
scanf("%d%d" , &n , &m);
for(i = 1 ; i <= n ; i ++ ) scanf("%lld" , &a[i]) , sum[i] = sum[i - 1] + a[i];
for(i = 1 ; i <= n ; i ++ ) f[i][1] = m * sum[i] * sum[i] - 2 * sum[n] * sum[i];
for(i = 2 ; i <= m ; i ++ )
{
l = r = 0 , d = i & 1;
for(j = 1 ; j <= n ; j ++ )
{
while(l < r && y(q[l + 1] , d ^ 1) - y(q[l] , d ^ 1) < 2 * m * sum[j] * (sum[q[l + 1]] - sum[q[l]])) l ++ ;
f[j][d] = y(q[l] , d ^ 1) - 2 * m * sum[j] * sum[q[l]] + m * sum[j] * sum[j] - 2 * sum[n] * sum[j];
while(l < r && (y(j , d ^ 1) - y(q[r] , d ^ 1)) * (sum[q[r]] - sum[q[r - 1]]) < (sum[j] - sum[q[r]]) * (y(q[r] , d ^ 1) - y(q[r - 1] , d ^ 1))) r -- ;
q[++r] = j;
}
}
printf("%lld
" , f[n][m & 1] + sum[n] * sum[n]);
return 0;
}