T1:求方程ax+by=c的解的个数,若超过65535则输出ZenMeZheMeDuo
( T<=10000 -1,000,000 <= a,b,c <= 1,000,000 )
这个形式? 一看不就是扩展欧几里得吗? ——by 冯神
然而群我数论最菜......
这个形式?一看不就是特判水分加暴力吗? ——by me
考场上一脸懵比,面向数据编程水了60分......
那说说正解,先想到exgcd,然后脑子……#@¥@&%¥%&%¥@#%……一通乱转,便有了算法雏形
exgcd求一般情况解 + 一大堆特判
先看一般情况:
我们可以用exgcd求出 ax + by = gcd(a,b) 的一组解,而且根据裴蜀定理可以知道,当且仅当 gcd(a,b) | c 时原方程有解
当有解时,再由exgcd的通解可以知道,解的分布情况应该是一次函数上一些位于第一象限的离散整点,且每隔gcd(a,b)出现一次(如图)
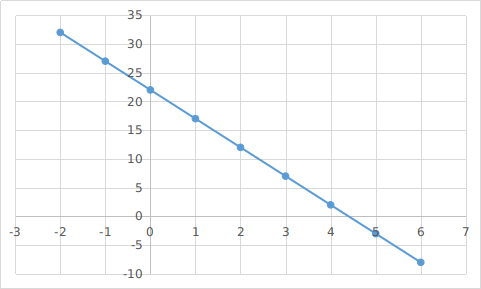
位于一次函数上?那就好办了,只要找到第一象限内最高点和最低点就可以用差值除以gcd(a,b)计算出答案了
那特判的情况呢?
某大佬指出,a、b、c 三个数分别有正、零、负三种情况,只要分33种情况讨论就好了
%¥&@%¥@#%&
不过真正写的时候可以先将三个数全转为正数,然后再打个标记,再exgcd之后再同时反转 (x,a) , (y,b) 就可以了
其他的特判就不多说了(不想说了)
最后说一句,只要特判打(shui)的好,正解都是浮云(好吧,其实是在掩饰我写不出正解的事实)

1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<algorithm> 5 #include<iostream> 6 #include<queue> 7 #include<vector> 8 #define ll long long 9 using namespace std; 10 11 int T; 12 13 ll a,b,c,x,y,g,tx,ty,bg,ed,ans; 14 15 void noanswer() 16 { 17 printf("0 "); 18 return; 19 } 20 void toomanyanswer() 21 { 22 printf("ZenMeZheMeDuo "); 23 return; 24 } 25 26 ll exgcd(ll aa,ll bb,ll &xx,ll &yy) 27 { 28 if(!bb) 29 { 30 xx=1;yy=0; 31 return aa; 32 } 33 ll g=exgcd(bb,aa%bb,yy,xx); 34 yy-=aa/bb*xx; 35 return g; 36 } 37 38 bool flaga,flagb; 39 40 int main() 41 { 42 scanf("%d",&T); 43 while(T--) 44 { 45 flaga=flagb=0; 46 scanf("%lld%lld%lld",&a,&b,&c); 47 if(c<0) a=-a,b=-b,c=-c; 48 if(!a&&!b&&!c) 49 {toomanyanswer();continue;} 50 if(!a&&!b&&c) 51 {noanswer();continue;} 52 53 if(a<0) flaga=1,a=-a; 54 if(b<0) flagb=1,b=-b; 55 56 g=exgcd(a,b,x,y); 57 58 if(c%g!=0) {noanswer();continue;} 59 if(flaga) a=-a,flaga=0,x=-x; 60 if(flagb) b=-b,flagb=0,y=-y; 61 62 if(!a) 63 { 64 if(y>0) toomanyanswer(); 65 else noanswer(); 66 continue; 67 } 68 if(!b) 69 { 70 if(x>0) toomanyanswer(); 71 else noanswer(); 72 continue; 73 } 74 75 if((a<0&&b>0)||(a>0&&b<0)) {toomanyanswer();continue;} 76 77 if(a<0) a=-a,b=-b,c=-c; 78 x=x*c/g,y=y*c/g; 79 a/=g,b/=g,c/=g; 80 tx=x%b; 81 while(tx<=0) tx+=b; 82 bg=(c-tx*a)/b; 83 ty=y%a; 84 while(ty<=0) ty+=a; 85 ed=ty; 86 if(bg<ed) {noanswer();continue;} 87 ans=(bg-ed)/a+1; 88 if(ans>65535) toomanyanswer(); 89 else printf("%lld ",ans); 90 } 91 return 0; 92 }
T2:在坐标平面上,从 ( 0,0 ) 到 ( n,m ) , 恰好走了T步的方案数 (在走够T步之前可以经过点 ( n,m ) ) , 输出答案对MOD取模之后的答案 ( T <= 100,000 -T <= n,m <= T 1 <= MOD <= 109+7) (MOD为若干互不相同质数的乘积)
哦? 能搜索吗? 不能。
能dp吗? 醒醒,看看 n,m 范围。
那就是数学了
一眼看出是组合数 (然并卵)
思考后会发现,对于一种方案,实际上是一个长度为T的指令序列,其中有上下左右四种指令
对于不同的指令序列,都有两种属性——1.各个指令的数量 2.排列的顺序
简单分析后会发现,若分别设上下左右的数量为a,b,c,d
则一种合法的恰能到达 ( n,m ) 的指令序列的数量属性一定满足:
a - b = m , d - c = n ( 不妨设 n,m 均为正 )
又因为 a+b+c+d = T
三个方程,四个未知数
于是我们只需要枚举任意一个未知数,复杂度 O ( T )
然后再用多重集合的排列来算方案数即可
愉快的做完了?
哦,××××,MOD不是质数!
怎么办啊???
想不出来,还好 %30 数据MOD保证是质数,水完再见
考完后有大佬分享正解
什么?竟然是中国剩余定理?
于是又学到一种新的思路
先将模数分解质因数,对于每一个质因子进行一次计算,最后再用中国剩余定理合并这些线性同余方程组。
(仅适用于满足——MOD为若干互不相同质数的乘积这一性质的取模运算)
那这就简单了,对于每一个质因子跑一次上述%30的算法,分别算出答案,最后再跑一下CRT就行了。
但要注意,对于组合数取模时,当模数小于组合数运算中的阶乘数时,不能直接用阶乘和阶乘逆元计算
因为大于模数的数阶乘后一定含有该模数,故值一定为0,且并不能通过乘以逆元来还原(并没有逆元)
这时就要用 Lucas 定理来计算
所以没了
ps:其实还有一种更通用的处理模数的思路,扩展Lucas,这样便可以一次计算出答案了
但这道题保证了MOD的特殊性,所以可以不用,但如果模数为任意自然数的话就必须用扩展Lucas了

1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<algorithm> 5 #include<iostream> 6 #include<queue> 7 #include<vector> 8 #include<cstdlib> 9 #define ll long long 10 using namespace std; 11 const int MAXT=100005; 12 13 ll t,n,m,p; 14 15 ll a,b,c,d; 16 17 void noanswer() 18 { 19 printf("0 "); 20 exit(0); 21 } 22 23 ll fac[MAXT],inv[MAXT]; 24 ll pri[30],ans[30],ptot; 25 26 ll qpow(ll x,ll k,ll id) 27 { 28 ll ret=1; 29 while(k) 30 { 31 if(k&1) ret=(ret*x)%pri[id]; 32 k>>=1; 33 x=(x*x)%pri[id]; 34 } 35 return ret%pri[id]; 36 } 37 38 void first(ll id) 39 { 40 ll lim=min((ll)t,pri[id]-1); 41 inv[0]=fac[0]=fac[1]=1; 42 for(int i=2;i<=lim;i++) 43 fac[i]=(fac[i-1]*i)%pri[id]; 44 inv[lim]=qpow(fac[lim],pri[id]-2,id); 45 for(int i=lim-1;i>=1;i--) 46 inv[i]=(inv[i+1]*(i+1))%pri[id]; 47 } 48 49 ll CRT() 50 { 51 ll mul=1,ret=0; 52 for(int i=1;i<=ptot;i++) 53 mul*=pri[i]; 54 ll x,y; 55 for(int i=1;i<=ptot;i++) 56 { 57 ll tmp=mul/pri[i]; 58 y=qpow(tmp,pri[i]-2,i); 59 ret=(ret+y*tmp%mul*ans[i]%mul)%mul; 60 } 61 return (ret%mul+mul)%mul; 62 } 63 64 ll C(ll x,ll y,ll id) 65 { 66 if(x<y) return 0; 67 return fac[x]*inv[y]%pri[id]*inv[x-y]%pri[id]; 68 } 69 70 ll Lucas(ll x,ll y,ll id) 71 { 72 if(x<y) return 0; if(!x) return 1; 73 return Lucas(x/pri[id],y/pri[id],id)*C(x%pri[id],y%pri[id],id)%pri[id]; 74 } 75 76 int main() 77 { 78 scanf("%lld%lld%lld%lld",&t,&p,&n,&m); 79 m=abs(m),n=abs(n); 80 if(t<n+m) noanswer(); 81 if((t&1)!=((n+m)&1)) noanswer(); 82 83 for(ll i=2;i*i<=p;i++) 84 if(p%i==0) 85 { 86 p/=i; 87 pri[++ptot]=i; 88 } 89 if(p>1) pri[++ptot]=p; 90 91 for(int i=1;i<=ptot;i++) 92 { 93 first(i); 94 for(int j=m;;j++) 95 { 96 a=j; 97 b=a-m; 98 c=(t-2*a+n+m)/2; 99 d=c-n; 100 if(d<0) break; 101 ans[i]=(ans[i]+Lucas(t,a,i)*Lucas(t-a,b,i)%pri[i]*Lucas(t-a-b,c,i)%pri[i])%pri[i]; 102 } 103 } 104 printf("%lld ",CRT()); 105 return 0; 106 } 107
T3:

考场上脑子没有,只打的60的暴力
结果发现正解就是优化的暴力
先说说暴力:
模拟,没了
再说说正解:
同一斜线的障碍存在一个vector(或set)里,每次搜的时候二分找下一个障碍,复杂度对了,没了
懂了吗? :)
那详细说说:
对于同一条斜线上的点,一定满足 x + y 或 x - y 为定值,如图:
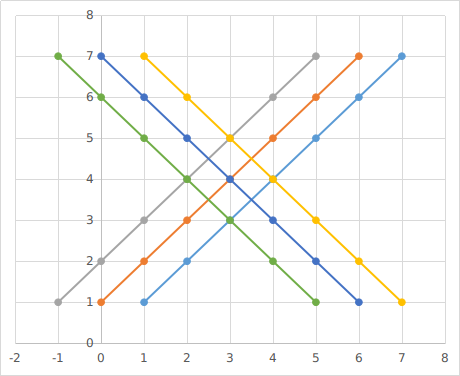
首先把斜线分成两种,一种为和相同,另一种为差相同
对于每个斜线开一个vector,将障碍点的横或纵坐标扔进去(横纵坐标均可,因为我们只需要一个可以比较其相对位置的元素)
那么这样就可以解决存不下图的问题了,
在搜索(模拟)的时候,只需要在当前斜线的vector中二分找到下一个障碍,再判断如何转向便可
而答案则是加上走过的格子即可
特别的,对于180o转向来说,最多只会出现两次,所以我们搜到的时候只需要跳出递归,再从起点反向搜索一遍,最后将答案-1(起点算了两遍)
但如果没有上述特殊情况,又怎么解决何时跳出的问题呢?
最开始想的是将起始点设为障碍,想想发现不太好写(可能吧)
之后发现其实从路径中的任何一个点出发都是等价的,所以我们可以在搜索前先走一步(找下一个障碍),然后在转向后的位置再开始搜索
这样之后一定可以搜到这个点,所以当搜到时return就行了
所以又没了

1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<algorithm> 5 #include<iostream> 6 #include<queue> 7 #include<vector> 8 #include<cstdlib> 9 #define ll long long 10 using namespace std; 11 const int MAXN=100005; 12 13 int n,m,k,bx,by,p,D,nx,ny; 14 15 ll ans; 16 17 int dx[5]={0,-1,-1,1,1},dy[5]={0,1,-1,1,-1}; 18 int pos[5]={0,4,3,2,1},pos1[5]={0,3,4,1,2},pos2[5]={0,2,1,4,3}; 19 20 char op[5]; 21 22 vector<int> t1[2*MAXN],t2[2*MAXN]; 23 // t1 -> 差 ; t2 -> 和 / 24 25 void first() 26 { 27 if(op[0]=='N') 28 { 29 if(op[1]=='E') p=1; 30 else p=2; 31 } 32 else 33 { 34 if(op[1]=='E') p=3; 35 else p=4; 36 } 37 for(int i=0;i<=n+1;i++) 38 { 39 t1[i-0+D].push_back(i); 40 t2[i+0].push_back(0); 41 t1[i-(m+1)+D].push_back(i); 42 t2[i+(m+1)].push_back(m+1); 43 } 44 for(int i=1;i<=m;i++) 45 { 46 t1[0-i+D].push_back(0); 47 t2[0+i].push_back(i); 48 t1[n+1-i+D].push_back(n+1); 49 t2[n+1+i].push_back(i); 50 } 51 for(int i=D-m-1;i<=D+n+1;i++) 52 sort(t1[i].begin(),t1[i].end()); 53 for(int i=0;i<=n+m+2;i++) 54 sort(t2[i].begin(),t2[i].end()); 55 } 56 57 bool flag; 58 59 void get_nxt(int x,int y,int o) 60 { 61 if(o==1) 62 { 63 int tmp=upper_bound(t2[x+y].begin(),t2[x+y].end(),y)-t2[x+y].begin(); 64 ny=t2[x+y][tmp]; 65 nx=x+y-ny; 66 ans+=ny-y; 67 } 68 if(o==2) 69 { 70 int tmp=upper_bound(t1[x-y+D].begin(),t1[x-y+D].end(),x)-t1[x-y+D].begin(); 71 nx=t1[x-y+D][tmp-1]; 72 ny=nx-x+y; 73 ans+=x-nx; 74 } 75 if(o==3) 76 { 77 int tmp=upper_bound(t1[x-y+D].begin(),t1[x-y+D].end(),x)-t1[x-y+D].begin(); 78 nx=t1[x-y+D][tmp]; 79 ny=nx-x+y; 80 ans+=nx-x; 81 } 82 if(o==4) 83 { 84 int tmp=upper_bound(t2[x+y].begin(),t2[x+y].end(),y)-t2[x+y].begin(); 85 ny=t2[x+y][tmp-1]; 86 nx=x+y-ny; 87 ans+=y-ny; 88 } 89 } 90 91 bool get(int x,int y) 92 { 93 int t=lower_bound(t1[x-y+D].begin(),t1[x-y+D].end(),x)-t1[x-y+D].begin(); 94 return t1[x-y+D][t]==x; 95 } 96 97 int cnt; 98 99 void dfs(int x,int y,int o) 100 { 101 if(x==bx&&y==by) 102 if(++cnt>1) return; 103 get_nxt(x,y,o); 104 if(get(nx,ny-dy[o])^get(nx-dx[o],ny)) 105 { 106 if(get(nx,ny-dy[o])) dfs(nx-dx[o],ny,pos1[o]); 107 else dfs(nx,ny-dy[o],pos2[o]); 108 } 109 else flag=1; 110 } 111 112 113 int main() 114 { 115 scanf("%d%d%d",&n,&m,&k); 116 D=max(n,m); 117 118 for(int i=1,aa,bb;i<=k;i++) 119 { 120 scanf("%d%d",&aa,&bb); 121 t1[aa-bb+D].push_back(aa); 122 t2[aa+bb].push_back(bb); 123 } 124 scanf("%d%d%s",&bx,&by,op); 125 first(); 126 127 get_nxt(bx,by,p); 128 if(get(nx,ny-dy[p])^get(nx-dx[p],ny)) 129 { 130 if(get(nx,ny-dy[p])) bx=nx-dx[p],by=ny,p=pos1[p]; 131 else bx=nx,by=ny-dy[p],p=pos2[p]; 132 } 133 else bx=nx-dx[p],by=ny-dy[p],p=pos[p]; 134 135 ans=0; 136 137 dfs(bx,by,p); 138 if(flag) cnt=0,dfs(bx,by,pos[p]),ans--; 139 printf("%lld ",ans); 140 return 0; 141 }
