题意
有一个n条横线m条竖线的长方形网格,求出(三点在整点上的)三角形的边上整点个数的期望。要求线性。
思考
ans=所有三角形的边经过的整点总个数÷三角形个数。方便起见,默认三角形的三条边是有顺序但没方向的。
记cnt(i,j)表示平面上第i个点与第j个点连线经过了几个整点,范围是( ],易证cnt(i,j)=gcd(|xi-xj|,|yi-yj|)。
1.三角形个数:
先枚举一条边,再看有多少个点能与它围成三角形。即
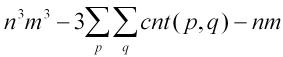
第一项表示所有的三个点组合,第二项表示去掉了退化成一条边的三角形,第三项表示去掉了退化成一个点的三角形。
2.整点个数:
还是枚举一条边,再看有多少个点能与它围成三角形。即
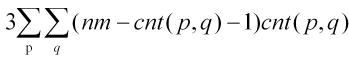
中间的减一表示把剩下的一个端点也扣掉,nm与它的差就是不在这个线段上的点的个数,并且每个有这条边的三角形贡献了cnt(p,q)。
但有不合法即退化成一条边的三角形。减去:
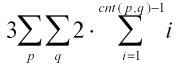
这个式子枚举了一个退化成一条边的三角形。中间的2表示决定了扣去的短点,那么剩下的部分只能从另一个端点开始枚举。此处强烈建议自己画图理解。
化简,得:
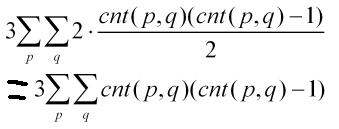
两式相减,得:
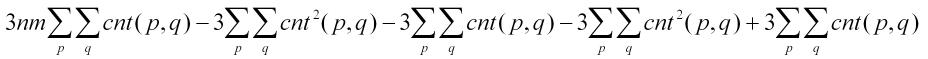
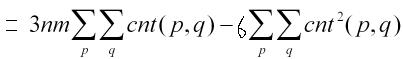
3.剩下的就是求解cnt和cnt2的事了。
考虑枚举|xp-xq|和|yp-yq|,则:
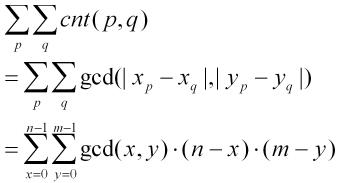
由于x=0和y=0能做到线性,只考虑x和y从1开始,则:
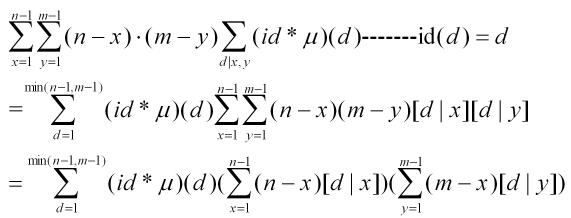
第一项是phi函数,第二项和第三项可以等差数列求和。
cnt平方也可以类似做。最后化为线性筛。
代码

1 #pragma GCC oprimize 2 2 #include<bits/stdc++.h> 3 #define mod 1000000007 4 #define G 500000004 5 using namespace std; 6 typedef long long int ll; 7 const ll maxn=5E6+5; 8 ll n,m; 9 ll ans1,ans2,ans,tot; 10 ll prime[maxn],size,phi[maxn],g[maxn]; 11 bool vis[maxn]; 12 inline void add(ll&x,ll y) 13 { 14 x=(x+y)%mod; 15 } 16 ll gcd(int x,int y) 17 { 18 if(x==0) 19 return y; 20 if(y==0) 21 return x; 22 return x%y==0?y:gcd(y,x%y); 23 } 24 void init() 25 { 26 phi[1]=g[1]=1; 27 for(ll i=2;i<=n;++i) 28 { 29 if(!vis[i]) 30 { 31 prime[++size]=i; 32 phi[i]=i-1; 33 g[i]=(i*i-1)%mod; 34 } 35 for(int j=1;j<=size&&prime[j]*i<=n;++j) 36 { 37 vis[prime[j]*i]=1; 38 if(i%prime[j]==0) 39 { 40 phi[prime[j]*i]=phi[i]*prime[j]; 41 g[prime[j]*i]=g[i]*prime[j]%mod*prime[j]%mod; 42 break; 43 } 44 phi[prime[j]*i]=phi[i]*(prime[j]-1); 45 g[prime[j]*i]=g[i]*(prime[j]*prime[j]%mod-1)%mod; 46 } 47 } 48 } 49 inline ll get(ll n,ll d) 50 { 51 ll m=(n-1)/d; 52 return (n*m%mod-d*m%mod*(m+1)%mod*G%mod+mod)%mod; 53 } 54 void solve1() 55 { 56 for(int i=1;i<=min(n-1,m-1);++i) 57 add(ans1,phi[i]*get(n,i)%mod*get(m,i)%mod*4); 58 for(ll x=0;x<=n-1;++x) 59 add(ans1,gcd(x,0)*(n-x)%mod*m%mod*2); 60 for(ll y=0;y<=m-1;++y) 61 add(ans1,gcd(y,0)*(m-y)%mod*n%mod*2); 62 } 63 void solve2() 64 { 65 for(int i=1;i<=min(n-1,m-1);++i) 66 add(ans2,g[i]*get(n,i)%mod*get(m,i)%mod*4); 67 for(ll x=0;x<=n-1;++x) 68 add(ans2,gcd(x,0)*gcd(x,0)%mod*(n-x)%mod*m%mod*2); 69 for(ll y=0;y<=m-1;++y) 70 add(ans2,gcd(y,0)*gcd(y,0)%mod*(m-y)%mod*n%mod*2); 71 } 72 ll qpow(ll x,ll y) 73 { 74 ll ans=1,base=x; 75 while(y) 76 { 77 if(y&1) 78 ans=ans*base%mod; 79 base=base*base%mod; 80 y>>=1; 81 } 82 return ans; 83 } 84 int main() 85 { 86 ios::sync_with_stdio(false); 87 cin>>n>>m; 88 init(); 89 solve1(); 90 solve2(); 91 add(tot,n*n%mod*n%mod*m%mod*m%mod*m%mod-3*ans1%mod-n*m%mod); 92 add(ans,3*n*m%mod*ans1%mod-6*ans2%mod); 93 add(tot,mod); 94 add(ans,mod); 95 cout<<ans*qpow(tot,mod-2)%mod<<endl; 96 return 0; 97 }
