DS博客作业03--树

0.PTA得分截图

1.本周学习总结（0-5分）

1.1 总结树及串内容

串的BFKMP算法

Bf算法：就是暴力(Brute Force)算法，是最最普通匹配算法，BF算法的思路就是将主串字符与待匹配串字符进行一一匹配，若相等，则继续比较主串字符的下一个字符和待匹配串的下一个字符；若不相等，则比较主串字符的下一个字符和待匹配串的第一个字符，如此比较下去，直到得出最后的匹配结果。BF算法就是进行暴力演算，所以时间复杂度大，最坏情况下要进行M(N-M+1)次比较，时间复杂度为O(MN)。

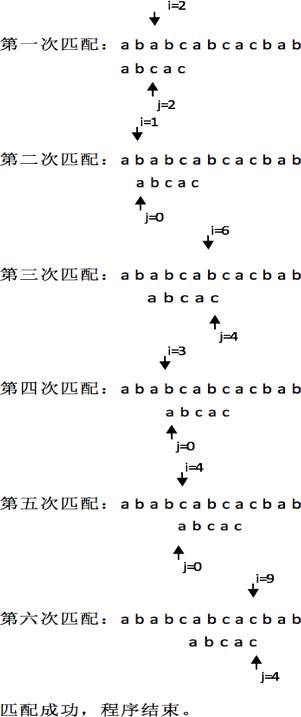
KMP算法：KMP 算法不回退指针 i，不走回头路（不会重复扫描母串），而是借助 next 数组中储存的信息把子串移到正确的位置继续匹配（相当于不断平移子串来进行匹配，母串指针不会后退），大大缩短匹配时间与匹配次数，时间复杂度只需 O(N)。

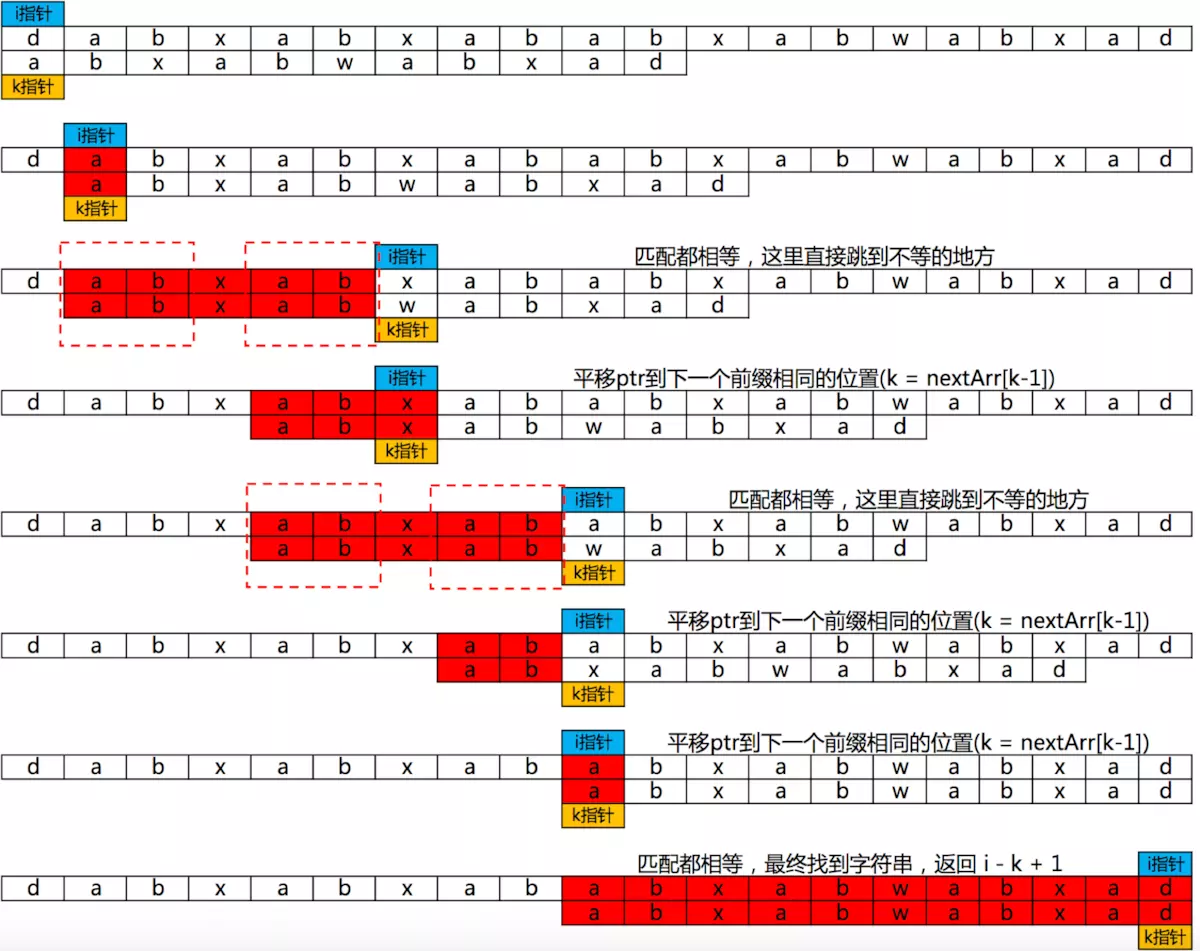
二叉树存储结构、建法、遍历及应用

二叉树存储结构：二叉树的存储结构分为顺序储存与链式存储，其中，顺序存储即用数组来存放二叉树数据，从数组下标1开始存放数据，所以下标为i的结点，其左孩子的下标为2i，右孩子的下标为2i+1，双亲的下标为i/2，如下图。顺序存储的优点是可以很方便地按层遍历以及找到双亲结点，但缺点为必须先定义好结点的最大数量，有时会浪费空间。

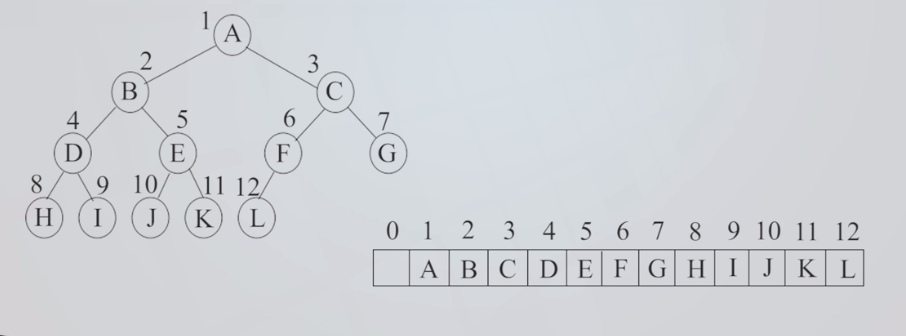
而链式存储即用结构体来实现二叉树，结构体内含3个域，即数据域，左右指针域，如下图。数据域用来存储数据，左右指针域用来指向左孩子与右孩子。链式结构可以很方便地找到左右孩子，但如果需要快速找到双亲结点，需要在结构体里加一个双亲指针。其缺点在于进行按层遍历时比较麻烦。

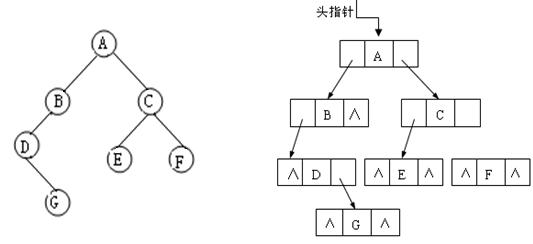
二叉树的建法：二叉树建法分为前序建二叉树，层序建二叉树

BiTree GetBiTree(char str[],int &i)//前序建二叉树
{
	if (i>=strLen||str[i]=='#')
	{
		return NULL;
	}
	BiTree P = new BiTNode;
	P->data = str[i];
	P->lchild = GetBiTree(str, ++i);
	P->rchild = GetBiTree(str, ++i);
	return P;
}

BiTree GetHiTree(ElemType str[], int i)//层序建二叉树
{
	BiTree Bt;

	if ( i >= strlen(str)||str[i] == '#')
	{
		return NULL;
	}

	Bt = new BiTNode;

	Bt->data = str[i];
	Bt->lchild = GetHiTree(str, 2 * i);
	Bt->rchild = GetHiTree(str, 2 * i+1);

	return Bt;
}

二叉树的遍历：二叉树的遍历有四种方式：前序遍历、中序遍历、后序遍历、层序遍历。
其中前序遍历：若树为空，则返回NULL。若不为空，先访问根节点，然后前序遍历左子树，再前序遍历右子树。
中序遍历：若树为空，则返回NULL。若不为空，先中序遍历根节点的左子树，然后是访问根节点，最后中序遍历根节点的右子树。
后序遍历：若树为空，则返回NULL。若不为空，先后序遍历根节点的左子树，然后后序遍历根节点的右子树，最后访问根节点。
层序遍历：若树为空，则返回NULL。若不为空，从树的第一层，也就是根节点开始访问，从上到下逐层遍历，在同一层中，按从左到右的顺序结点逐个访问。

二叉树的应用：

• 哈夫曼编码来源于哈夫曼树（给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为赫夫曼树(Huffman tree)。即带权路径长度最短的树），在数据压缩上有重要应用，提高了传输的有效性，详见《信息论与编码》。
• 海量数据并发查询二叉树复杂度是O(K+LgN)。二叉排序树就既有链表的好处，也有数组的好处， 在处理大批量的动态的数据是比较有用。
• C++ STL中的set/multiset、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。查找最大（最小）的k个数，红黑树，红黑树中查找/删除/插入，都只需要O(logk)。
• B-Tree，B+-Tree在文件系统中的目录应用。
• 路由器中的路由搜索引擎。

树的结构、操作、遍历及应用

树的结构：树的每个结点有零个或多个子结点，每一个非根结点有且只有一个双亲结点，除了根节点之外，每个子结点可以分为多个不相交的子树。结点的度指结点拥有的子树的个数，树的度指数中度最大的结点的度数。二叉树其实就是一棵特殊的树，一颗树的度和所有结点的度均为2的树。

树的操作：与二叉树类似，定义、查找、插入及删除等

树的遍历：与二叉树类似先序，后序，层序等

树的应用：

• B, B+树:广泛用于数据库(mysq|, oracle等)的索引。
• 字典树:用于海量文本词频统计，查询效率比哈希表还高。
• 生活中的树状结构有公司职级关系,国家省市区级联，族谱等等都有树结构形式!

线索二叉树

线索二叉树的介绍：对于n个结点的二叉树，在二叉链存储结构中有n+1个空链域，利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针，这些指针称为线索，加上线索的二叉树称为线索二叉树。这样既可以有效利用空间，又可以利用线索方便寻找到某结点的前驱或后继。

线索二叉树的结构：

typedef struct TNode
{
       ElemType data;                                   //结点数据
       struct BTNode *lchild, *rchild;                  //左右孩子指针
       int  ltag;                                       //左右标志
       int  rtal;
}BTNode, *BTree;

其中当ltag为0时lchild指向该结点的左孩子，为1时lchild指向该结点的前驱，当rtag为0时rchlid指向该结点的右孩子，为1时rchlid指向该结点的后继。前驱与后继看二叉树是以何种方式遍历，如：
1.先序

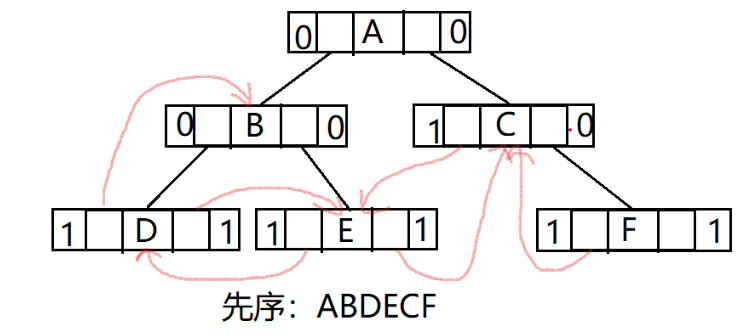
2.中序

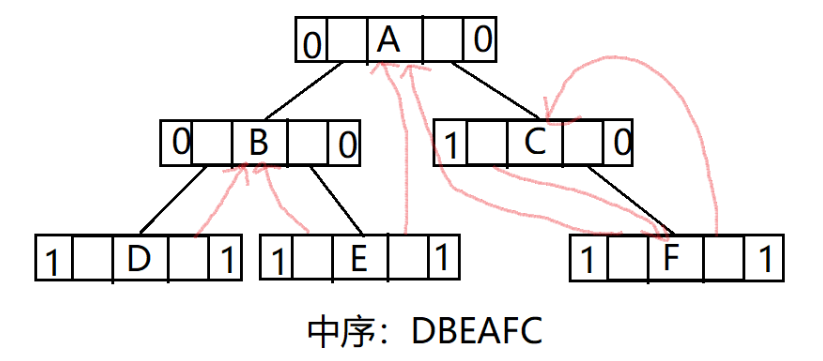
3.后续

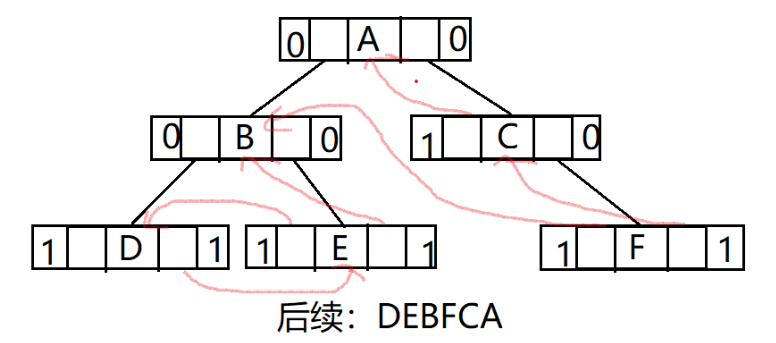
哈夫曼树

哈夫曼树介绍：给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度（WPL）达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近，权值较小的结点离根较远。

哈夫曼树的结构定义：

typedef struct
{
    int data;        //数据
    double weight;   //权值
    int parent;      //双亲指针
    int lchild;      //左孩子指针
    int rchild;      //右孩子指针
}HTNode; 

哈夫曼树的代码实现：

void HuffmanTree(int n, HufTNode ht[])//求哈夫曼树
{
	int i, j, k;
	int lNode, rNode;
	int Min1, Min2;                     
	for (i = n; i < 2 * n - 1; i++)
	{
		Min1 = Min2 = 1001;          
		lNode = rNode = -1;
		ht[i].parent = -1;              
		for (k = 0; k < i; k++)
		{
			if (ht[k].parent == -1)         		
			{
				if (ht[k].data < Min1)      		
				{
					Min2 = Min1;
					rNode = lNode;
					Min1 = ht[k].data;
					lNode = k;
				}
				else if (ht[k].data < Min2)    		
				{
					Min2 = ht[k].data;
					rNode = k;
				}
			}
		}
		ht[lNode].parent = i;
		ht[rNode].parent = i;
		ht[i].data = ht[lNode].data + ht[rNode].data;
		ht[i].lchild = lNode;
		ht[i].rchild = rNode;                     
	}

哈夫曼树的应用：可以用哈夫曼编码来对传输数据进行处理，使数据的文本量减小。

并查集

并查集的介绍：并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。就是判断某棵子树是否属于某棵树的子树，若是，则将其在最后一个公共根节点处合并，若不是，则将前者与后者以相同地位合并

并查集的应用：电脑文件夹的目录树等。

1.2.谈谈你对树的认识及学习体会。

• 对树的认识：树是一种很特殊的结构，通过不断分支的特点可以实现诸如：海量数据并发查询、哈夫曼树、红黑树等运用。

• 学习体会：在本阶段的学习里，认识了树以及其特殊形态二叉树这一特殊的数据结构，其实树也是通过上个学期的基础知识，利用一些特殊的结构手法来实现的，通过对树这类结构的学习，不仅能巩固以前的知识，也能让我们对计算机语言的特性与功能有更深入的认识。

2.阅读代码（0--5分）

2.1 题目及解题代码

题目：

解题代码：

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
      dfs(root);
      return root;
    }
private:
    void dfs(TreeNode* root){
        if(root){
            swap(root->left, root->right);
            dfs(root->left);
            dfs(root->right);
        }
    }
};

2.1.1 该题的设计思路

该题用递归的方法就可以快速又简单地解决了，可以递归遍历每个结点，将每个结点的左右孩子互换，即可求出本题
算法时间复杂度：O(n)
空间复杂度：S(n)=O(1)

2.1.2 该题的伪代码

void dfs(TreeNode* root){
        if(root不为空){
            交换root的左右孩子;
            dfs(root->left);
            dfs(root->right);
        }
    }

2.1.3 运行结果

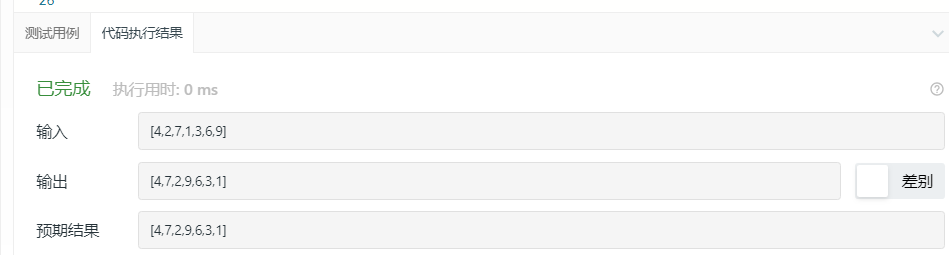
2.1.4分析该题目解题优势及难点。

该题的思路很好，要求我们对树的结构有着清晰的认识，也对树的递归操作的简单应用进行了考察，这是本题的主要考点。

2.2 题目及解题代码

题目：

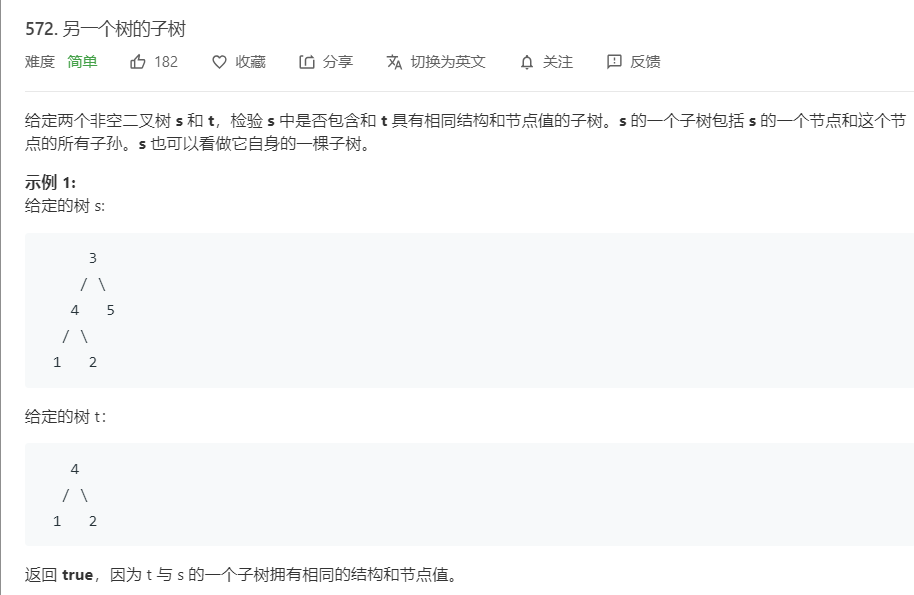
解题代码：

bool isSubtree(TreeNode* s, TreeNode* t) {
        if (!s) return false;
        return isSubtree(s->left, t) || SameTree(s, t) || isSubtree(s->right, t);
    }

    bool SameTree(TreeNode* s, TreeNode* t) {
        if (s == nullptr && t == nullptr) return true;
        if (s == nullptr || t == nullptr) return false;
        return s->val == t->val && SameTree(s->left, t->left) && SameTree(s->right, t->right);
    }

2.2.1 该题的设计思路

该题应该先找到子串的根节点，再依次进行比较，但解题代码运用递归，遍历的主树的每一个结点与子树进行比较，直到找到子树
算法时间复杂度：O(n)=n
空间复杂度：S(n)=O(1)

2.2.2 该题的伪代码

bool isSubtree(TreeNode* s, TreeNode* t) {
        if (s为空) return false;
        return isSubtree(s->left, t) || SameTree(s, t) || isSubtree(s->right, t);
    }

    bool SameTree(TreeNode* s, TreeNode* t) {
        if (s与t都是空指针) return true;
        if (有且只有一个不是空指针) return false;
        return s->val == t->val && SameTree(s->left, t->left) && SameTree(s->right, t->right);
    }

2.2.3 运行结果

2.2.4分析该题目解题优势及难点。

该题目的解题优势是运用了两个递归，并且很好的运用了return，将代码量精简到内容部分只有5行，可以说构思非常巧妙了，该题的难点在于如何利用递归去同时遍历比较两棵树。

2.3 题目及解题代码

题目：

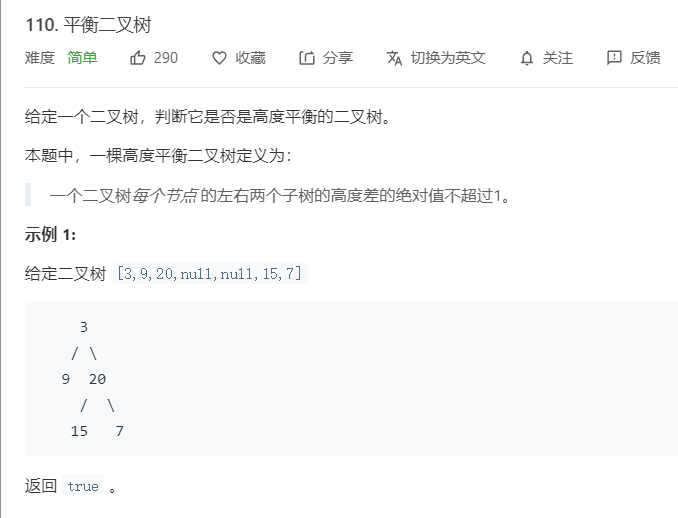
解题代码：

class Solution {
public:
    int leftnum,rightnum;
    bool flag=true;
    void dfs_sum(TreeNode* root,int &sum){//求节点有多深
        if(!root) return ;
        int temp;
        sum+=1;
        temp=sum;
        dfs_sum(root->left,sum);//分别求左右节点
        int m=sum;
        sum=temp;
        dfs_sum(root->right,sum);//分别求左右节点
        int n=sum;
        sum=max(m,n);//返回两个节点中较大的那个sum值
    }
    int getnum(TreeNode* root){
        int sum=0;
        dfs_sum(root,sum);
        return sum;//返回长度
    }
    void checkflage(TreeNode* root){
        if(!root) return ;
        leftnum = getnum(root->left);
        rightnum = getnum(root->right);
        if(abs(leftnum-rightnum)>1)
        {   
            flag=false;
        }
        checkflage(root->left);
        checkflage(root->right);

    }
    bool isBalanced(TreeNode* root) {
        checkflage(root); 
        if(flag==true)
            return true;
        else
            return false;
    }
};

2.3.1 该题的设计思路

链表题目，请用图形方式展示解决方法。同时分析该题的算法时间复杂度和空间复杂度。

2.3.2 该题的伪代码

    int leftnum,rightnum;
    bool flag=true;
    void dfs_sum(TreeNode* root,int &sum){//求节点有多深
        if(root为空) return ;
        int temp;
        sum+=1;
        temp=sum;
        遍历左子树dfs_sum(root->left,sum);//分别求左右节点
        int m=sum;
        sum=temp;
        遍历右子树dfs_sum(root->right,sum);//分别求左右节点
        int n=sum;
        sum=max(m,n);//返回两个节点中较大的那个sum值
    }
    int getnum(TreeNode* root){
        int sum=0;
        求root的长度dfs_sum(root,sum);
        return sum;//返回长度
    }
    void checkflage(TreeNode* root){
        if(root为空) return ;
        求左子树高度leftnum = getnum(root->left);
        求右子树高度rightnum = getnum(root->right);
        if(高度差大于1)
        {   
            flag=false;
        }
        往下遍历左子树checkflage(root->left);
        往下遍历右子树checkflage(root->right);

    }
    bool isBalanced(TreeNode* root) {
        checkflage(root); 
        if(flag==true)
            return true;
        else
            return false;
    }

2.3.3 运行结果

2.3.4分析该题目解题优势及难点。

该题解题分装了多个函数，各个函数的关系较为紧密，整体性强。同时运用了递归来遍历检查各个结点是否符合条件，代码很精简。该题的难点在于能否正确找到左右子树的高度。

2.4 题目及解题代码

题目：

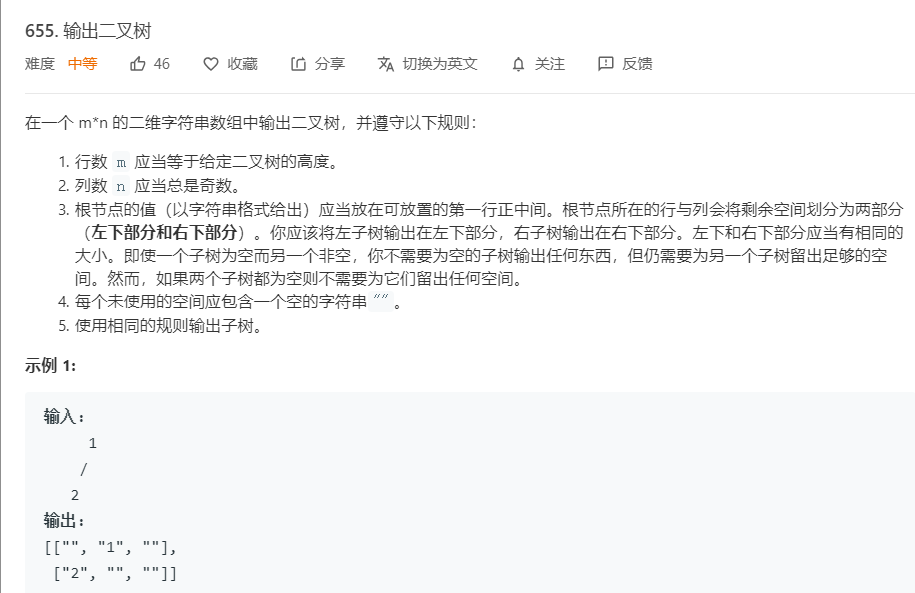
解题代码：

class Solution {
public:
    int getHeight(TreeNode* root)
    {
        if(root)
        {
            return max(getHeight(root->left),getHeight(root->right))+1;
        }
        return 0;
    }
    void fill(TreeNode* root,vector<vector<string>>& res,int l,int r,int hight)
    {
        if(root)
        {
            int mid=(l+r)/2;
            res[hight][mid]=to_string(root->val);
            fill(root->left,res,l,mid-1,hight+1);
            fill(root->right,res,mid+1,r,hight+1);
        }
    }
    vector<vector<string>> printTree(TreeNode* root) {
        int m=getHeight(root);
        int n=pow(2,m);
        vector<vector<string>> res(m,vector<string>(n-1,""));
        fill(root,res,0,n-1,0);
        return res;
    }
};

2.3.1 该题的设计思路

该题需要我们先求得树的高度，以此先建一个空的二维vector容器，初始化为“”，然后再一个个地将数据放入
算法时间复杂度：O(2n)
空间复杂度：S(n)=O(n^2)

2.4.2 该题的伪代码

vector<vector<string>> printTree(TreeNode* root) {
        int m=root高度
        int n=m平方（即需要的容器大小）
        定义一个二维的vector容器res，大小为n-1且初始化为“”
        递归函数fill(root,res,0,n-1,0)将数据放入
        return res;
    }
void fill(TreeNode* root,vector<vector<string>>& res,int l,int r,int hight)
    {
        if(root不为空)
        {
            int mid=(l+r)/2;
            res[hight][mid]=to_string(root->val);
            递归左子树fill(root->left,res,l,mid-1,hight+1);
            递归右子树fill(root->right,res,mid+1,r,hight+1);
        }
    }

2.4.3 运行结果

2.4.4分析该题目解题优势及难点。

该题用到了还没正式学习的新知识vector容器，由我个人理解而言，我觉得vector容器很像数组，但是能够进行类似链表的操作，将数组与链表各自的优点结合起来，对一些数据的处理非常有用。
该题难点在于如何选择正确的结构来存储树中的信息，既能方便录入也能方便输出，而vector很好地做到了这一点。