动态规划思想
注意:子串和子序列的区别
子串一定时连续的,子序列不一定是连续的

首先清楚dp数组的含义
定义:dp[i]表示以nums[i]这个数结尾的最长递增子序列的长度
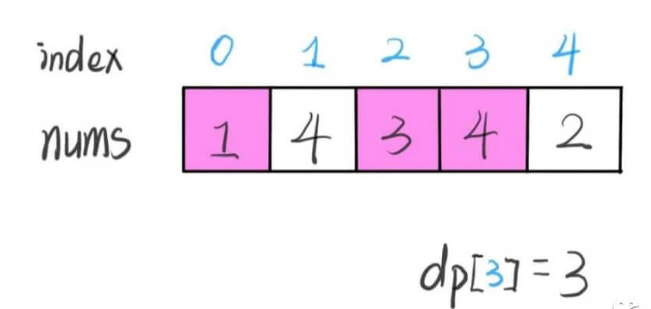
因为nums[3]=4,最长递增子序列为1,3,4,所以长度为3即dp[3]=3
既然是递增子序列,只要找到前面那些结尾比4小的子序列,然后把4接到最后,就可以形成一个新的递增子序列,长度加1
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
# 初始化dp数组为1
dp = [1] * len(nums)
for i in range(len(nums)):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j]+1)
res = 0
for i in range(len(dp)):
res = max(res, dp[i])
return res

class Solution:
def findNumberOfLIS(self, nums: List[int]) -> int:
if not nums:
return 0
# length表示以x为结尾的最长递增子序列的长度
length = [1 for _ in range(len(nums))]
# count 表示以x为结尾的最长递增子序列的个数
count = [1 for _ in range(len(nums))]
for i in range(len(nums)):
for j in range(i):
if nums[i] > nums[j]:
# 在初始化的length表基础上,正常都是length前面的值小于等于length后面的值(初始化为1)
if length[j] >= length[i]:
length[i] = length[j] + 1
count[i] = count[j]
# 如果遇到这个i前面两个相同的值,第二次进入这个条件时,这个i已经是做过length[i] = length[j] + 1,即有两个长度相同的子序列
elif length[j] + 1 == length[i]:
count[i] += count[j]
res = 0
# 找最长递增子序列,要在length中找长度最长的子序列个数之和
maxSub = max(length)
for i in range(len(nums)):
if length[i] == maxSub:
res += count[i]
return res