回溯算法三：经典问题实现（m-着色、n-皇后、Hamilton回路、子集和）

目录

• 一、m-着色问题
• 二、 n-皇后问题
• 三、Hamilton回路
• 四、子集和

问题分析过程，可以参考：回溯算法一：算法介绍与经典问题分析
算法框架分析过程，可以参考：回溯算法二：算法框架与实现

一、m-着色问题

根据问题分析以及回溯框架简化，代码实现如下：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int isPartial(int *G, int n, int *x, int k)
{
    for (int i = 0; i < k; i++) {
        // 根据邻接表判断两个节点之间是否相邻，再进一步判断其配色是否相同,x中按顺序保存各节点的配色
        if ((G[i * n + k] == 1) && (x[i] == x[k])) {
            return 0;
        }
    }
    return 1;
}

// 递归过程，x与k同时变化，其他均为定值
void generalExplore(int *G, int n, int *colors, int m, int *x, int k)
{
    int i;
    // 完全解判断：k为当前解长度，n为完整解的最大长度
    if (k >= n) {
        for (int i = 0; i < n; i++) {
            printf("%d ", x[i]);
        }
        printf("
");
        return;
    }
    // 无解退出
    if (k >= n) {
        return;
    }
    // 递归遍历，回溯过程
    for (int i = 0; i < m; i++) {
        // 当前节点的取值集合，根据问题分析，通常可以确定
        x[k] = colors[i];
        // 判断部分解逻辑复杂，建议抽取函数
        if (isPartial(G, n, x, k)) {
            generalExplore(G, n, colors, m, x, k + 1);
        }
    }
}

int main(void)
{
    // G为邻接矩阵，n为解向量长度，color为颜色集合，m为颜色种类，x为解向量空间，k为当前解的个数[0, n-1]
    int n = 5;
    int G[25] = {0, 1, 1, 0, 0,
                 1, 0, 0, 1, 1,
                 1, 0, 0, 1, 1,
                 0, 1, 1, 0, 1,
                 0, 1, 1, 1, 0};
    int m = 3;
    int colors[] = {1, 2, 3};
    int *x = (int*)calloc(n, sizeof(int));
    int k = 0;

    generalExplore(G, n, colors, m, x, k);
    while(1);
    return 0;
}

测试结果：

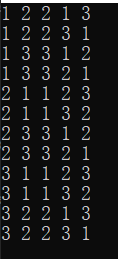
二、 n-皇后问题

该代码实现与着色问题仅修改了部分解判断条件和函数入参，可见框架适应性较强：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// x[i]表示每行棋子的列位置，k表示最新添加的棋子索引，即当前处理的第k行的棋子位置问题（k从0开始）
int isPartial(int n, int *x, int k)
{
    int diff;
    for (int i = 0; i < k; i++) {
        // 判断新增的位置与历史位置是否满足规则：不同行、不同列、不同斜线
        diff = x[i] - x[k];
        // 列位置相同——同列；列号之差等于行号之差——对角线；遍历处理[0,k-1]行，不可能同行
        if (diff == 0 || (diff == i - k) || (diff == k - i)) {
            return 0;
        }
    }
    return 1;
}

// 递归过程，x与k同时变化，其他均为定值
void nQueens(int n, int *locations, int *x, int k)
{
    int i;
    // 完全解判断：k为当前解长度，n为完整解的最大长度
    if (k >= n) {
        for (int i = 0; i < n; i++) {
            printf("%d ", x[i]);
        }
        printf("
");
        return;
    }
    // 无解退出
    if (k >= n) {
        return;
    }
    // 递归遍历，回溯过程
    for (int i = 0; i < n; i++) {
        // 当前节点的取值集合，根据问题分析，通常可以确定
        x[k] = locations[i];
        // 判断部分解逻辑复杂，建议抽取函数
        if (isPartial(n, x, k)) {
            nQueens(n, locations, x, k + 1);
        }
    }
}

int main(void)
{
    // n为棋盘规模，x为解向量空间，k为当前解的个数[0, n-1]
    int n = 4;
    int k = 0;
    // x[i]表示第i行上，皇后对应的列的位置
    int *x = (int*)calloc(n, sizeof(int));
    int locations[] = {0, 1, 2, 3, 4};
    
    // n为棋盘规模，locations为棋盘位置集合（列），x为解向量空间，k为当前解的个数[0, n-1]
    nQueens(n, locations, x, k);
    while(1);
    return 0;
}

测试结果：

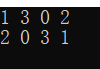
结果表明，4皇后有两种方案，[1, 3, 0, 2]表示每行的列的序号，实际摆放如下：

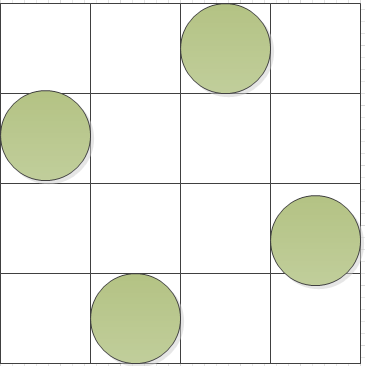
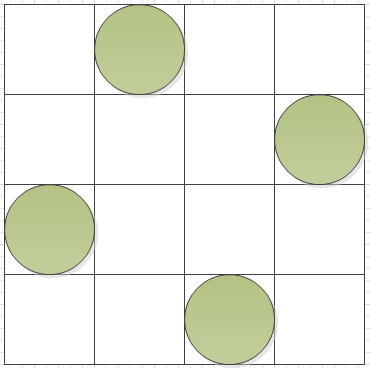
leetcod51：n-皇后问题源码

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 将解决方案x转化成输出格式
void printSolution (int n, int *x, char ***res, int* returnSize, int** returnColumnSizes)
{
    // 二维数组的处理
    res[*returnSize] = (char **)malloc(n * sizeof(char *));
    for (int i = 0; i < n; i++) {
        res[*returnSize][i] = (char *)malloc((n + 1) * sizeof(char));
        memset(res[*returnSize][i], 0, n + 1);
        for (int j = 0; j < n; j++) {
            if (j == x[i]) {
                res[*returnSize][i][j] = 'Q';
            } else {
                res[*returnSize][i][j] = '.';
            }
        }
    } 
    (*returnSize)++;
}

// x[i]表示每行棋子的列位置，k表示最新添加的棋子索引，即当前处理的第k行的棋子位置问题（k从0开始）
int isPartial(int n, int *x, int k)
{
    int diff;
    for (int i = 0; i < k; i++) {
        // 判断新增的位置与历史位置是否满足规则：不同行、不同列、不同斜线
        diff = x[i] - x[k];
        // 列位置相同——同列；列号之差等于行号之差——对角线；遍历处理[0,k-1]行，不可能同行
        if (diff == 0 || (diff == i - k) || (diff == k - i)) {
            return 0;
        }
    }
    return 1;
}

// 递归过程，x与k同时变化，其他均为定值
void nQueens(int n, int *locations, int *x, int k, char ***res, int* returnSize, int** returnColumnSizes)
{
    int i;
    // 完全解判断：k为当前解长度，n为完整解的最大长度
    if (k >= n) {
        for (int i = 0; i < n; i++) {
            // printf("%d ", x[i]);
        }
        // printf("
");
        // 输出结果处理
        printSolution (n, x, res, returnSize, returnColumnSizes);
        return;
    }
    // 无解退出
    if (k >= n) {
        return;
    }
    // 递归遍历，回溯过程
    for (int i = 0; i < n; i++) {
        // 当前节点的取值集合，根据问题分析，通常可以确定
        x[k] = locations[i];
        // 判断部分解逻辑复杂，建议抽取函数
        if (isPartial(n, x, k)) {
            nQueens(n, locations, x, k + 1, res, returnSize, returnColumnSizes);
        }
    }
}
char *** solveNQueens(int n, int* returnSize, int** returnColumnSizes)
{
    int maxSize = n * n * 10 + 1;
    // 返回结果: returnSize-行向量，解法数量；returnColumnSizes——列向量，
    char ***res = (char ***)malloc(maxSize * sizeof(char **));
    *returnSize = 0;
    // *returnColumnSizes[returnSize] = 0;

    // n为棋盘规模，x为解向量空间，k为当前解的个数[0, n-1]
    int k = 0;
    // x[i]表示第i行上，皇后对应的列的位置
    int *x = (int*)calloc(n, sizeof(int));
    // locations表示列的取值集合
    int *locations = (int*)calloc(n, sizeof(int));
    for (int i = 0; i < n; i++) {
        locations[i] = i;
    }
    
    // n为棋盘规模，locations为棋盘位置集合（列），x为解向量空间，k为当前解的个数[0, n-1]
    nQueens(n, locations, x, k, res, returnSize, returnColumnSizes);
    // printf("returnSize[%d]
", *returnSize);
    *returnColumnSizes = (int *)malloc(*returnSize * sizeof(int));
    for (int i = 0; i < *returnSize; i++) {
        (*returnColumnSizes)[i] = n; 
    }

    return res;
}

测试结果：

三、Hamilton回路

代码实现：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int isPartial(int *G, int n, int *x, int k)
{
    // 条件一：新增点不重复
    for (int i = 0; i < k; i++) {
        if (x[i] == x[k]) {
            return 0;
        }
    }
    // 条件二：根据邻接表判断新增节点与前一个节点之间是否直连G[x[k - 1]][x[k]]
    if (G[n * x[k - 1] + x[k]] == 0) {
        return 0;
    }
    return 1;
}

// 递归过程，x与k同时变化，其他均为定值
void getHamilton(int *G, int n, int *nodes, int *x, int k)
{
    int i;
    // 完全解判断：k为当前解长度，n为完整解的最大长度
    // 同时判断最后添加的一个数，是否与起点直连(x[k]为节点号，G[x[k]][0] 即表示该点与起点是否直连)
    if (k >= n && G[x[k - 1] * n] == 1) {
        for (int i = 0; i < n; i++) {
            printf("%d -> ", x[i]);
        }
        printf("0
");
        return;
    }
    // 无解退出
    if (k >= n) {
        return;
    }
    // 递归遍历，回溯过程
    for (int i = 0; i < n; i++) {
        // 当前节点的取值集合，根据问题分析，通常可以确定
        x[k] = nodes[i];
        // 判断部分解逻辑复杂，建议抽取函数
        if (isPartial(G, n, x, k)) {
            getHamilton(G, n, nodes, x, k + 1);
        }
    }
}

测试代码：

int main(void)
{
    // G为邻接矩阵，n为解向量长度，nodes为节点集合，x为解向量空间，k为当前解的个数[0, n-1]
    int n = 5;
    int G[25] = {0, 1, 1, 1, 0,
                 1, 0, 1, 0, 1,
                 1, 1, 0, 1, 0,
                 1, 0, 1, 0, 1,
                 0, 1, 0, 1, 0};
    int nodes[] = {0, 1, 2, 3, 4};
    int *x = (int*)calloc(n, sizeof(int));
    // 从节点0开始，经过一段路径后，回到节点0
    x[0] = 0;
    int k = 1;

    getHamilton(G, n, nodes, x, k);
    while(1);
    return 0;
}

示例无向图：

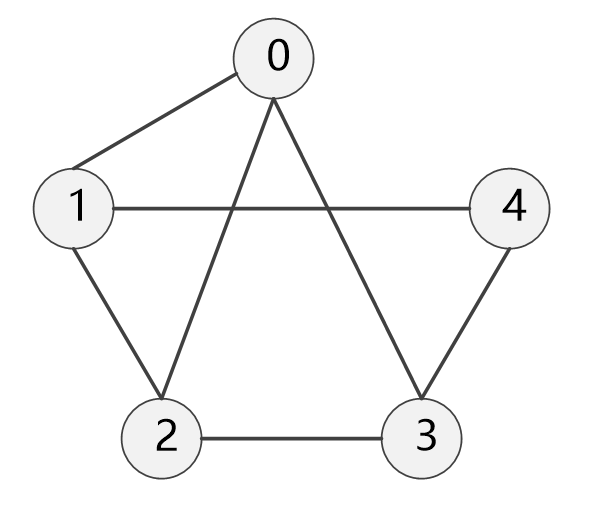
测试结果：

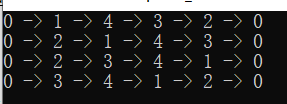
四、子集和

代码实现：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int getTempSum(int *G, int n, int *x, int k)
{
    int sum = 0;
    for (int i = 0; i < k; i++) {
        // 根据邻接表判断两个节点之间是否相邻，再进一步判断其配色是否相同,x中按顺序保存各节点的配色
        sum += G[i] * x[i];
    }
    return sum;
}

// 递归过程，x与k同时变化，其他均为定值
void subSetSum(int *G, int n, int m, int *x, int k)
{
    int i;
    // 完全解判断：k为当前解长度，n为完整解的最大长度
    if (getTempSum(G, n, x, k) == m) {
        for (int i = 0; i < k; i++) {
            if (x[i] == 1) {
                printf("%d ", G[i]);
            }
        }
        printf("
");
        return;
    }
    // 无解退出
    if (k >= n) {
        return;
    }
    // 递归遍历，回溯过程
    for (int i = 0; i < 2; i++) {
        // 子集问题，取值固定为0、1，可以简化
        x[k] = i;
        if (getTempSum(G, n, x, k) <= m) {
            subSetSum(G, n, m, x, k + 1);
        }
    }
}

int main(void)
{
    // G为邻接矩阵，n为解向量长度，m为子集和，x为解向量空间，k为当前解的个数[0, n-1]
    int n = 4;
    int G[25] = {1, 2, 3, 4};
    int m = 7;
    int *x = (int*)calloc(n, sizeof(int));
    int k = 0;

    subSetSum(G, n, m, x, k);
    while(1);
    return 0;
}

测试结果：