
题目大意:
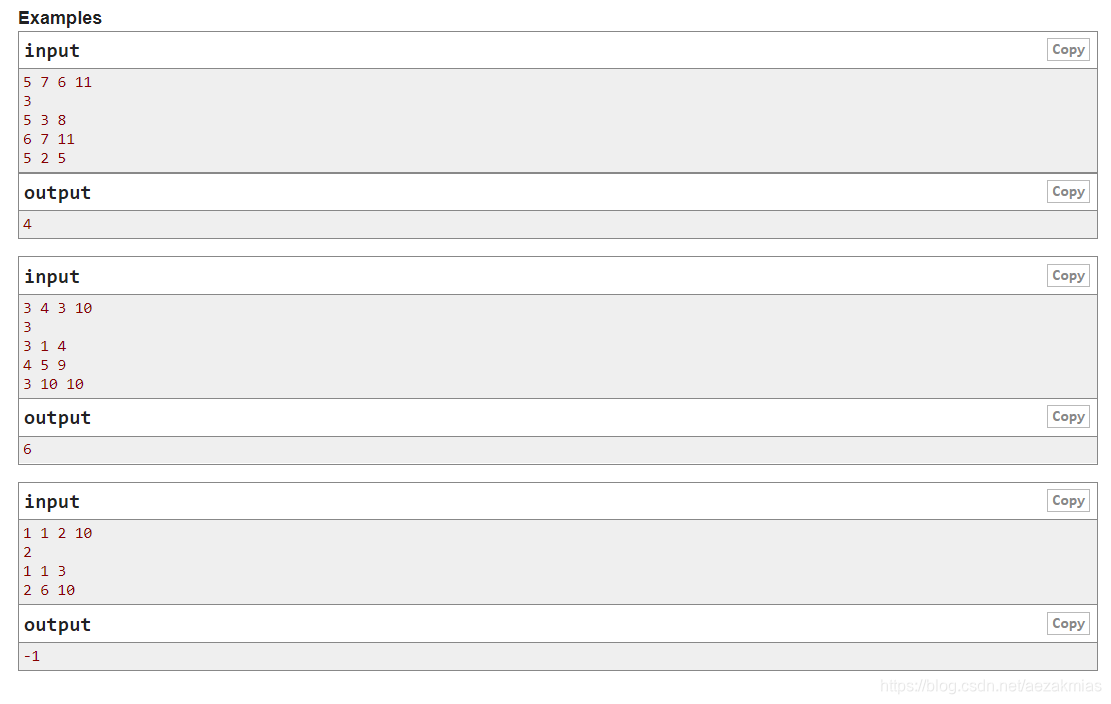
首先你有一个109 * 109 大小的棋盘,第一行输入四个数,两两一组分别代表起点和终点,第二行输入一个 n ,接下来n行每行输入3个数r a b ,表示在第 r 行中,第a列到第b列中的格子是可以走的,从起点开始,你可以向八个方向移动,要求输出从起点到终点的最小步数,如果不能到达则输出 -1。
解题思路:
求最短步数就是标准的bfs模板,棋盘是1e9 * 1e9 的,用数组存是放不下的,可以借助一个map和pair<int, int>来映射哪些路可以走和哪些路已经走过了,队列中存放x, y, s(步数),这样就可以实现bfs了,套用bfs模板即可。
Code:
#pragma GCC optimize(2)
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <cstring>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 5050;
int dir[][2] = {0, 1, 0, -1, 1, 0, -1, 0, 1, -1, -1, 1, 1, 1, -1, -1};
map<pii, int> mp;
map<pii, int> vis;
struct node { int x, y, s; };
int x, y, xx, yy, ans = -1;
void bfs()
{
queue<node > q;
q.push({x, y, 0});
vis[make_pair(x, y)] = 1;//第一个点已经走过
while (!q.empty())
{
auto t = q.front();
q.pop();
if (t.x == xx && t.y == yy)
{
ans = t.s;
return;
}
for (int k = 0; k < 8; k ++)
{
int nx = t.x + dir[k][0];
int ny = t.y + dir[k][1];
if (!mp[make_pair(nx, ny)] || vis[make_pair(nx, ny)])//判断是否走过以及该点是否可以走,如果不符合条件则continue;
continue;
vis[make_pair(nx, ny)] = 1;//标记走过
q.push({nx, ny, t.s + 1});//该点入队
}
}
return;
}
int main()
{
ios::sync_with_stdio(false);
cin >> x >> y >> xx >> yy;
int n;
cin >> n;
while (n--)
{
int r, a, b;
cin >> r >> a >> b;//(r, a) -> (r, b) 都是可以走的
if (a > b) swap(a, b);
for (int i = a; i <= b; i ++)
mp[make_pair(r, i)] = 1;//mp用于存放该点是否可以走,1表示能走
}
bfs();
cout << ans << endl;
return 0;
}