Description
No wonder the old bookcase caved under the massive piles of books Tom had stacked on it. He had better build a new one, this time large enough to hold all of his books. Tomfinds it practical to have the books close at hand when he works at his desk. Therefore, he is imagining a compact solution with the bookcase standing on the back of the desk. Obviously, this would put some restrictions on the size of the bookcase, it should preferably be as small as possible. In addition, Tom would like the bookcase to have exactly three shelves for aesthetical reasons.
Wondering how small his bookcase could be, he models the problem as follows. He measures the height hi and thickness ti of each book i and he seeks a partition of the books in three non-empty sets S1, S2, S3 such that
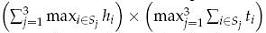is minimized, i.e. the area of the bookcase as seen when standing in front of it (the depth needed is obviously the largest width of all his books, regardless of the partition). Note that this formula does not give the exact area of the bookcase, since the actual shelves cause a small additional height, and the sides cause a small additional width. For simplicity, we will ignore this small discrepancy. Thinking a moment on the problem, Tom realizes he will need a computer program to do the job.
Input
Output
Sample Input
2 4 220 29 195 20 200 9 180 30 6 256 20 255 30 254 15 253 20 252 15 251 9
Sample Output
18000 29796
题意：求出将n本书全部放在三层书架上，求出最大宽度和高度和的最小值
思路： dp[i][j][k]表示前i本书第二层高度为j, 第三层高度为k的总高度的最小值
状态转移方程为：
dp[i][j][k]= { dp[i-1][j][k]; //第i本书放在第一层；
dp[i-1][j][k]+book[i].h; //j==0第二层还没有书本
dp[i-1][j+boo[i].w][k]; //第i本书放在第二层且非第二层的第一本书
dp[i-1][j][k]+book[i].h; //k==0第三层还没有书本
dp[i-1][j][k+book[i].w]; //第i本书放在第三层且非第三层的第一本书
}
那么就可以考虑给空间优化，dp设成二维数组 dp[i][j]表示后两层宽度为i, j中高度的最小值；
第二层放的书取决于前一层的宽度；第三层放的书取决于前两层；
将高度按照由大到小排序， 宽度有小到大；
但是高度和要求整体最优最后枚举所有的宽度的总和，求出总面积的最小；
dp[j][k]={
j==0, a=book[i].h; dp[j+book[i].w][k]=min(dp[j+book[i].w][k], d[[j][k]+a);
k==0, a=book[i].h; d[j][k+book[i].w]=min(d[j][k+book[i].w], d[[j][k]+a)
}
代码如下：
View Code
#include<stdio.h> #include<string.h> #include<iostream> #include<algorithm> using namespace std; #define N 71 #define M 31 #define Max 999999 int dp[N*M][N*M]; struct Book { int h, w; }; int cmp(Book x, Book y) { if(x.h!=y.h) return x.h>y.h; return x.w<y.w; } int main() { int T, i, j, n, sum, k; scanf("%d", &T); while(T--) { Book book[N]; scanf("%d", &n); sum=0; for(i=1; i<=n; i++) { scanf("%d%d", &book[i].h, &book[i].w); sum+=book[i].w; } sort(book+1, book+n+1, cmp); for(i=0; i<=sum; i++) for(j=0; j<=sum; j++) dp[i][j]=Max; dp[0][0]=0; int noww=0; for(i=2; i<=n; i++) { for(j=noww; j>=0; j--) { for(k=noww; k>=0; k--) { if(dp[j][k]==Max) continue; if(noww-j-k<0) continue; int a=0; if(j==0) a=book[i].h; dp[j+book[i].w][k]=min(dp[j+book[i].w][k], dp[j][k]+a); a=0; if(k==0) a=book[i].h; dp[j][k+book[i].w]=min(dp[j][k+book[i].w], dp[j][k]+a); } } noww+=book[i].w; } int minnum=Max; for(j=1; j<=noww; j++) { for(k=1; k<=noww; k++) { if(dp[j][k]==Max) continue; if(sum-j-k<=0) continue; int maxw=max(j, k); maxw=max(maxw, sum-j-k); minnum=min(minnum, maxw*(dp[j][k]+book[1].h)); } } printf("%d\n", minnum); } }