该系列为DR_CAN自动控制原理视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 从稳态误差入手
先回顾一下稳态误差:
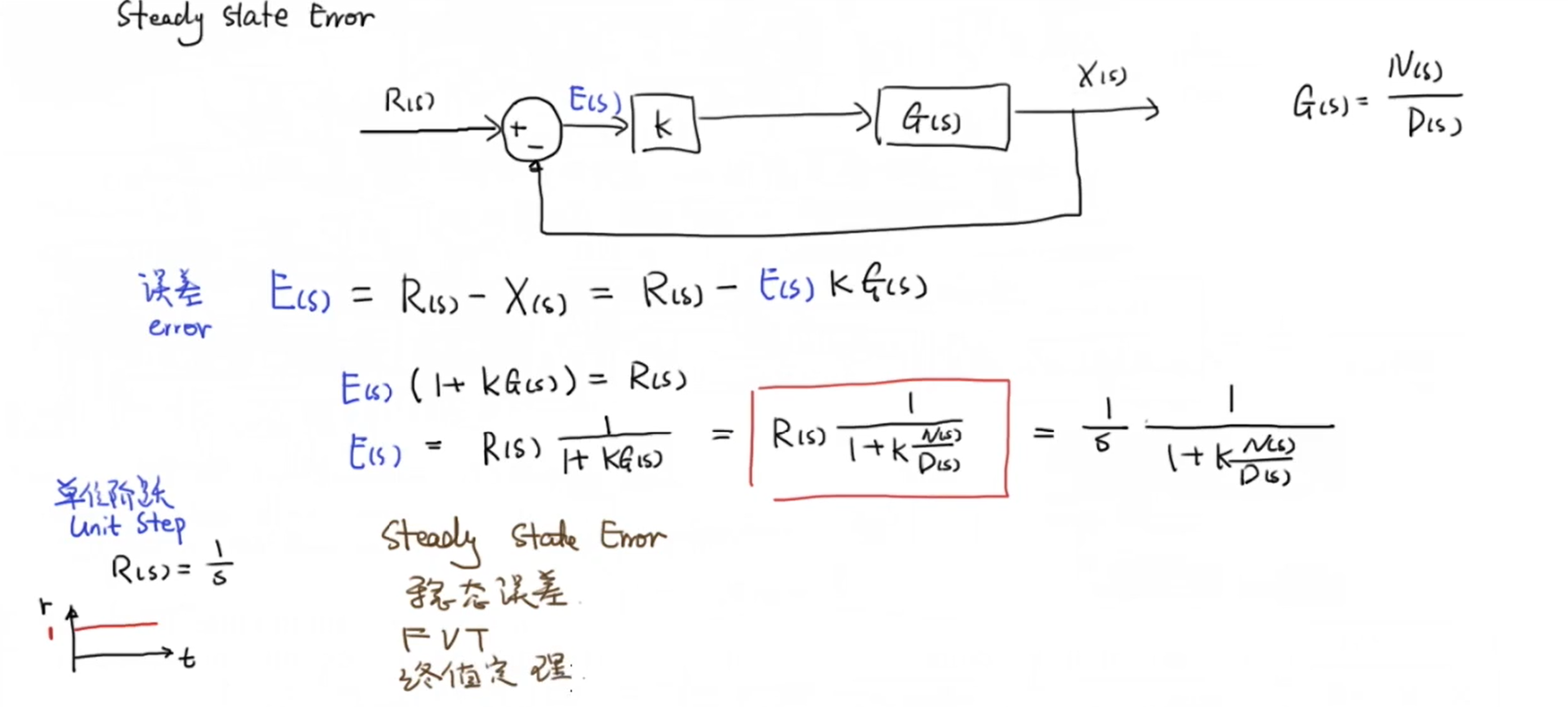
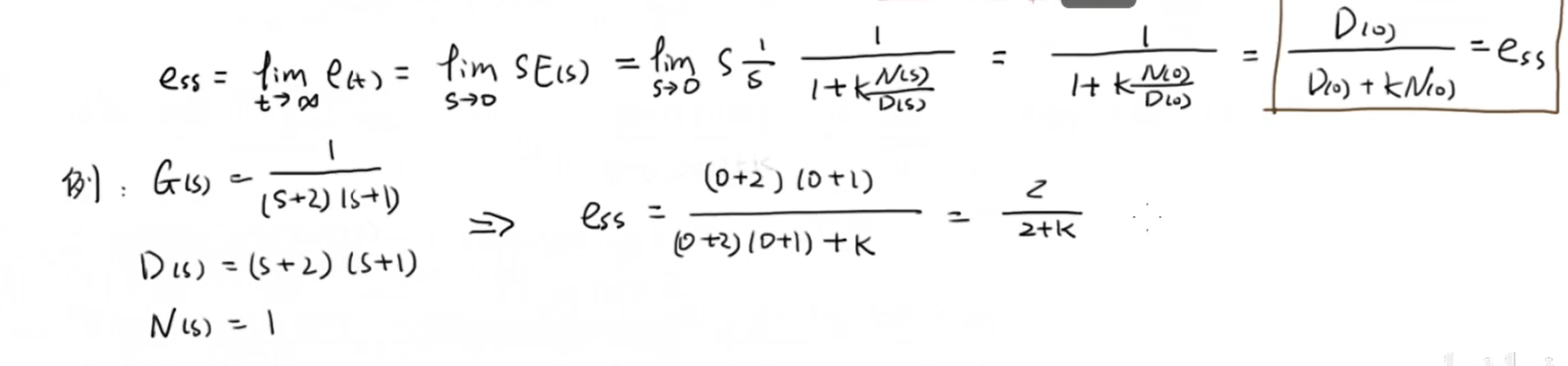
以上是比例控制下的稳态误差,现在我们添加一个补偿器(下标c),然后更新一下误差的计算公式:
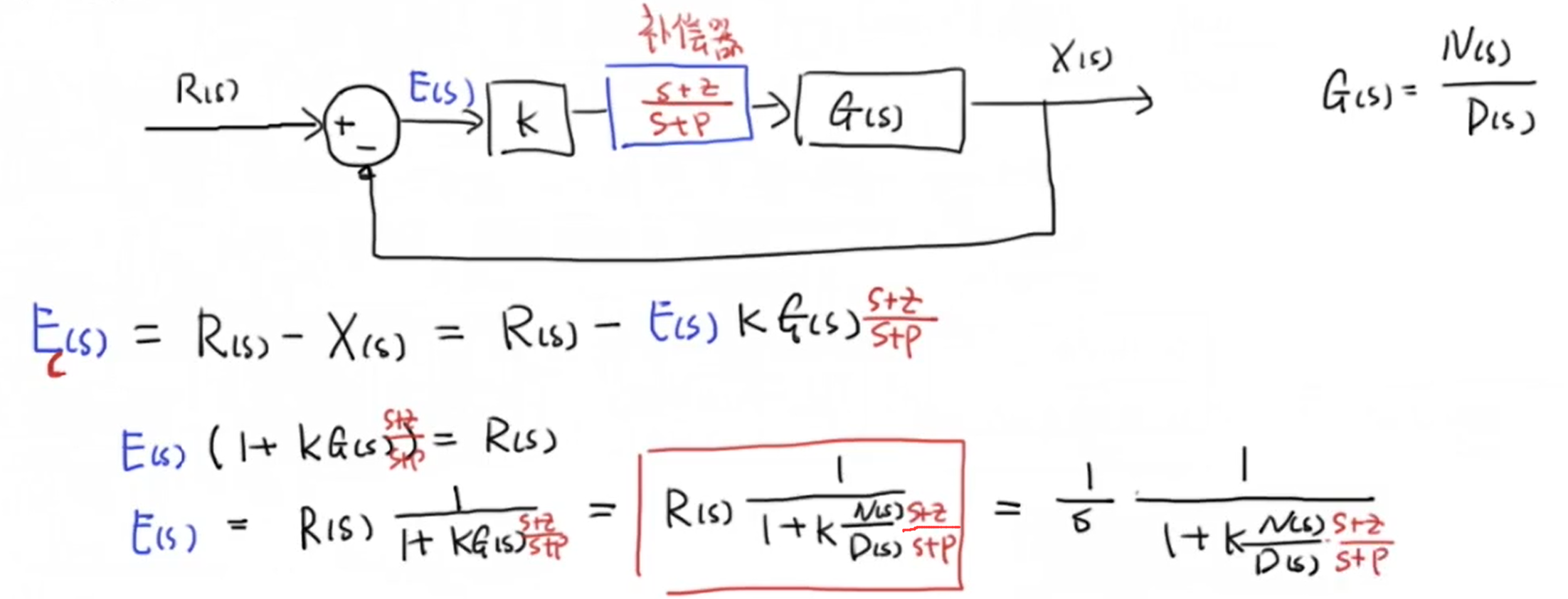

然后我们对比一下这两种情况下的稳态误差表达式:

我们的最终目的是消除稳态误差,因此我们希望 (frac{z}{p}) 要尽可能的大,这样我们可以得到滞后补偿器(Lag Compensator):
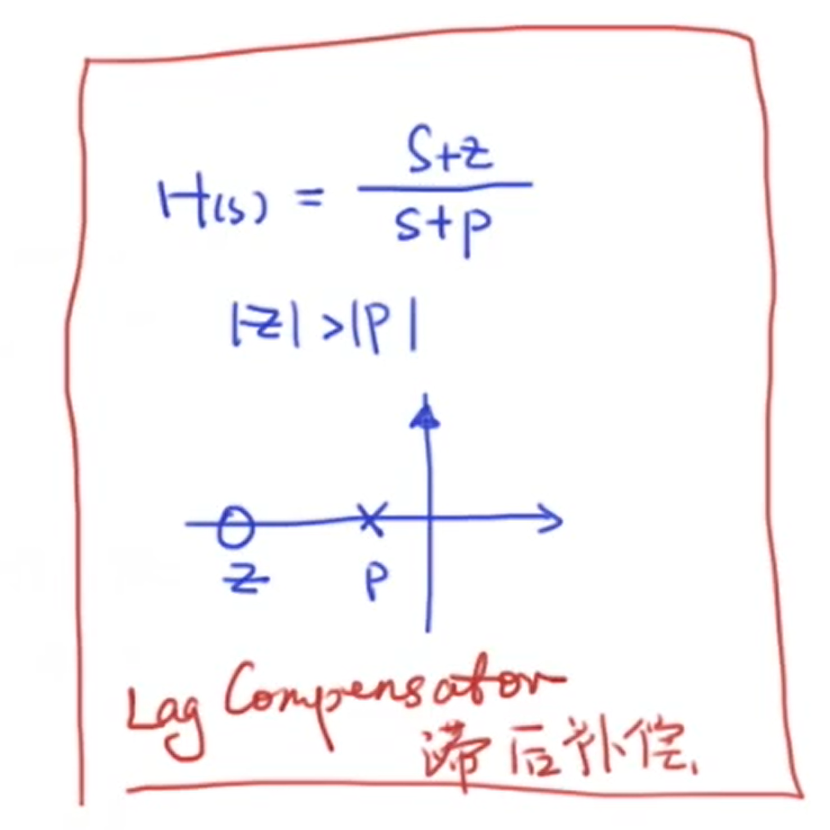
当 (P=0) 时,稳态误差可以被完全消除,此时的滞后补偿器的表达式就可以写成PI控制器的形式:
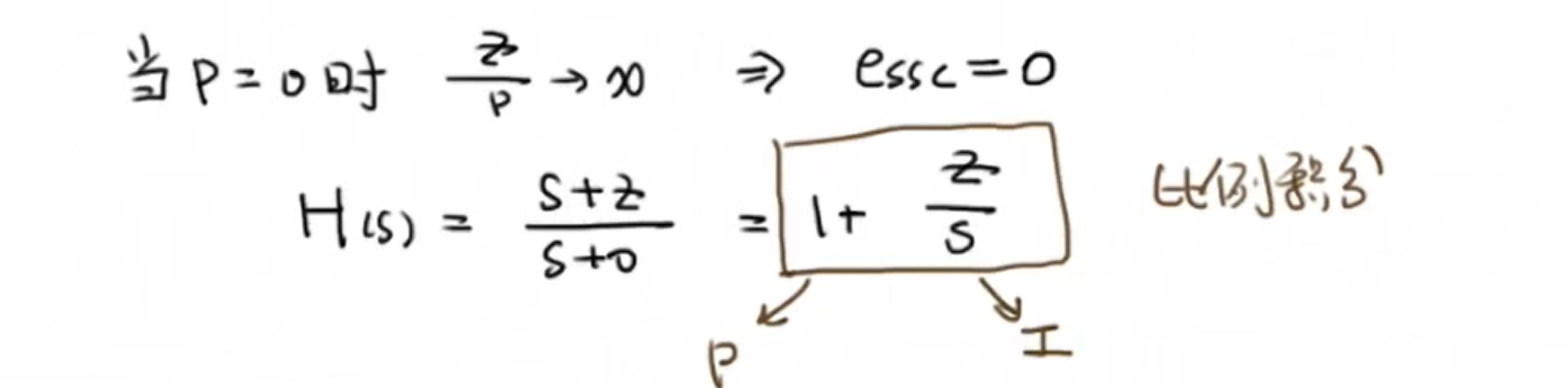
2 应用滞后补偿器
这里还是用上面那个例子,现在我们的目标是设计 (H(s)) 使系统稳态误差为0.1:
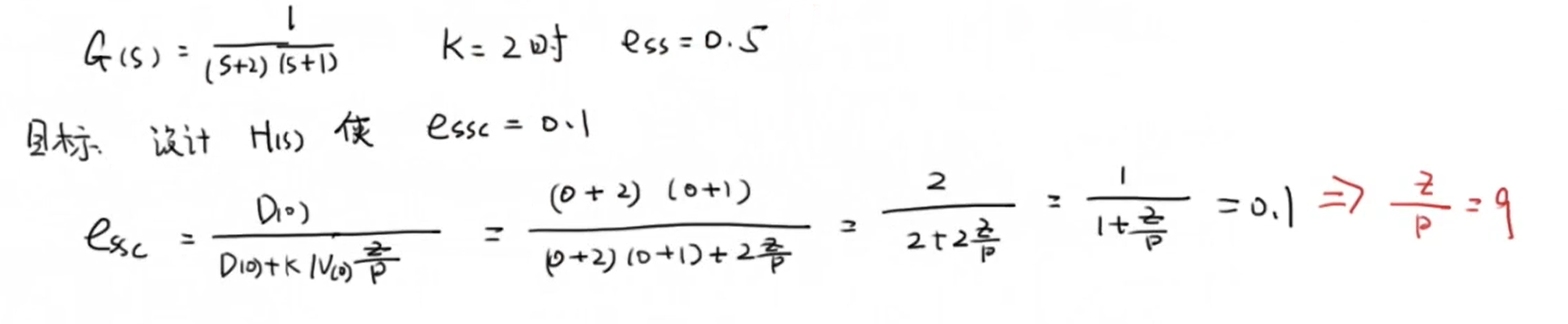
现在我们得到了补偿器零点和极点的比值,接下来我们需要找到合适的具体值。我们在simulink中搭建出三种情况,分别是无补偿器和两种有补偿器的情况:
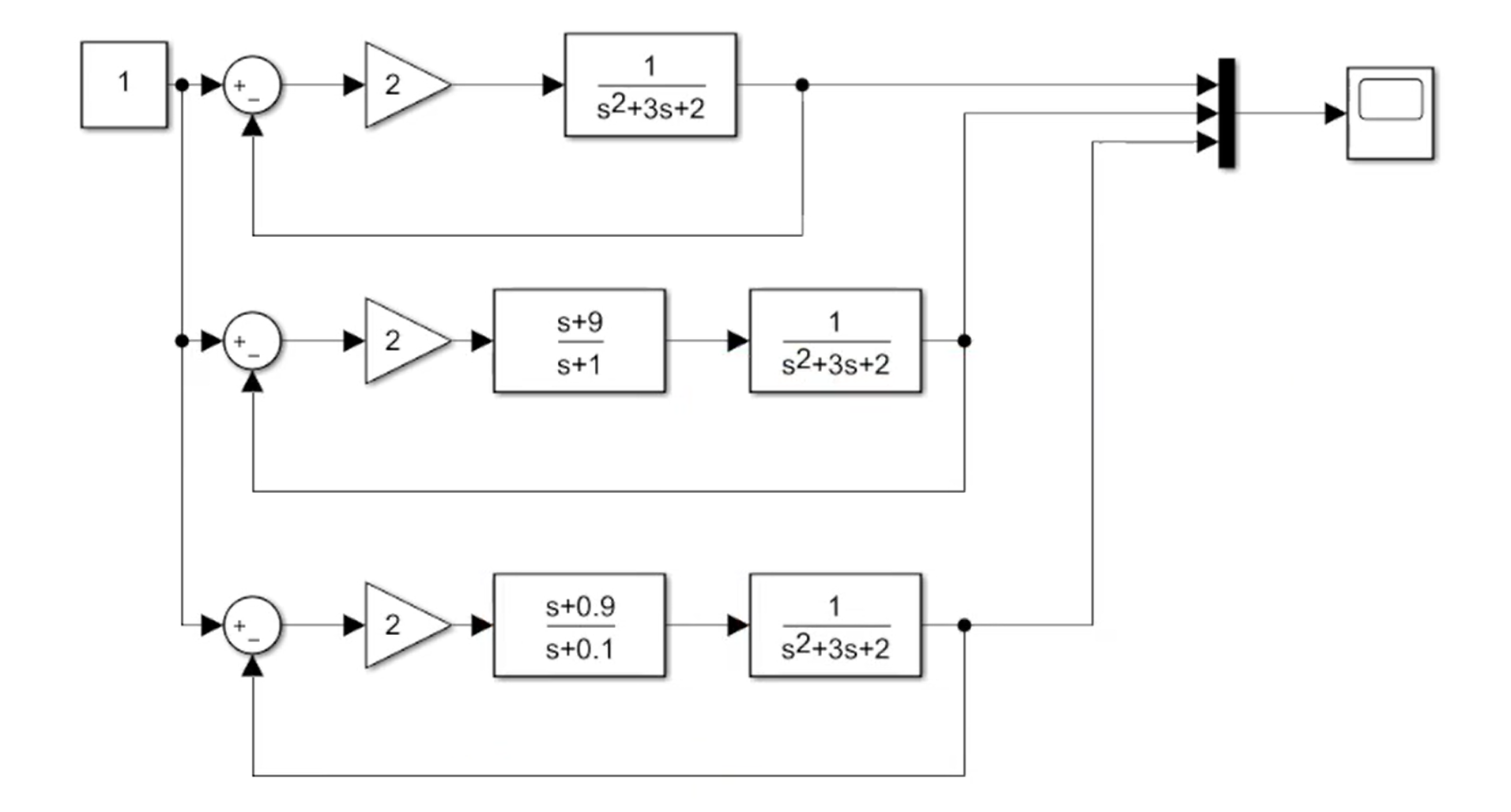
结果如下:
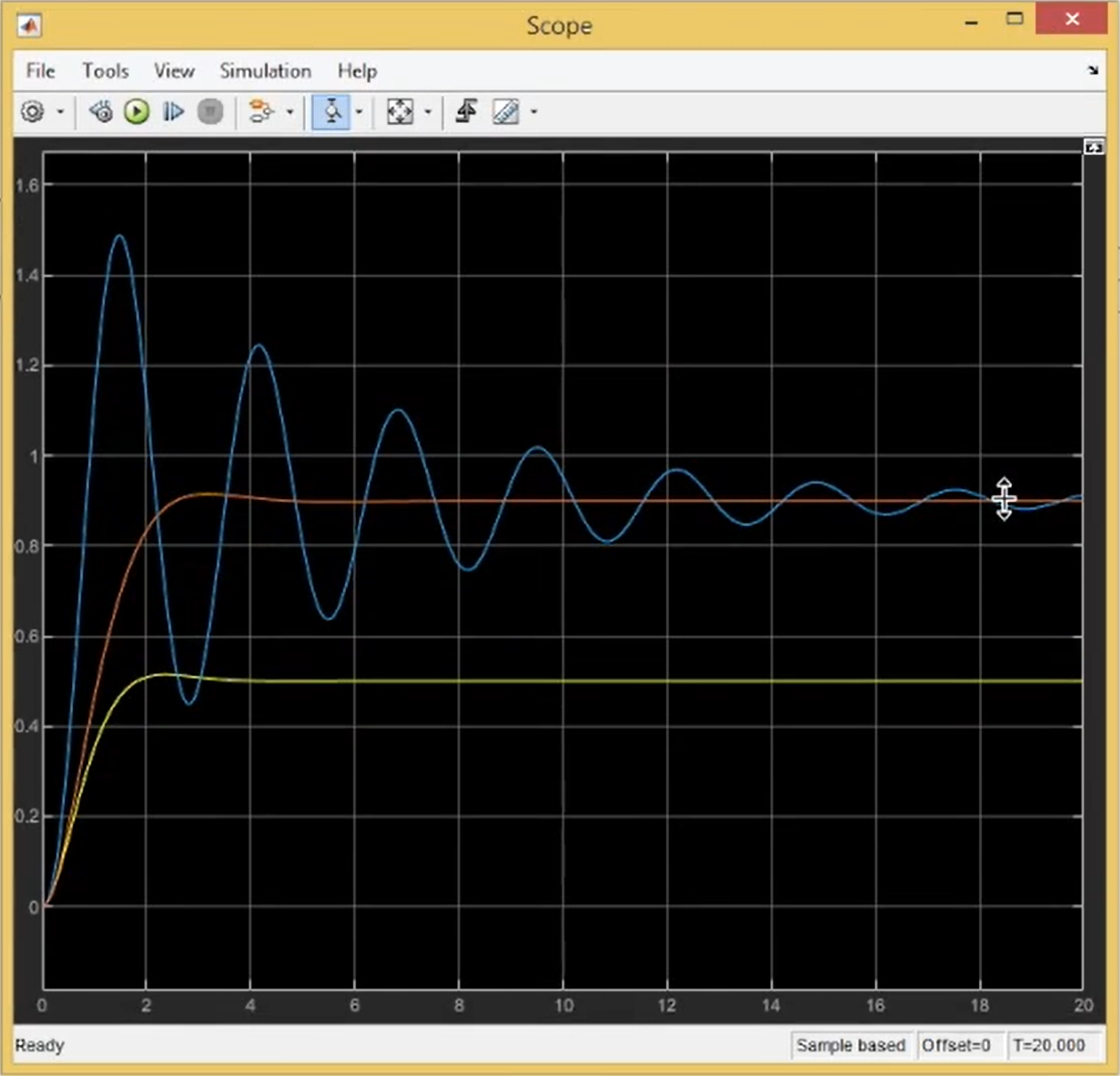
其中黄线是没有补偿器的情况,蓝线为零点为9极点为1的情况,红线为零点为0.9极点为0.1的情况。
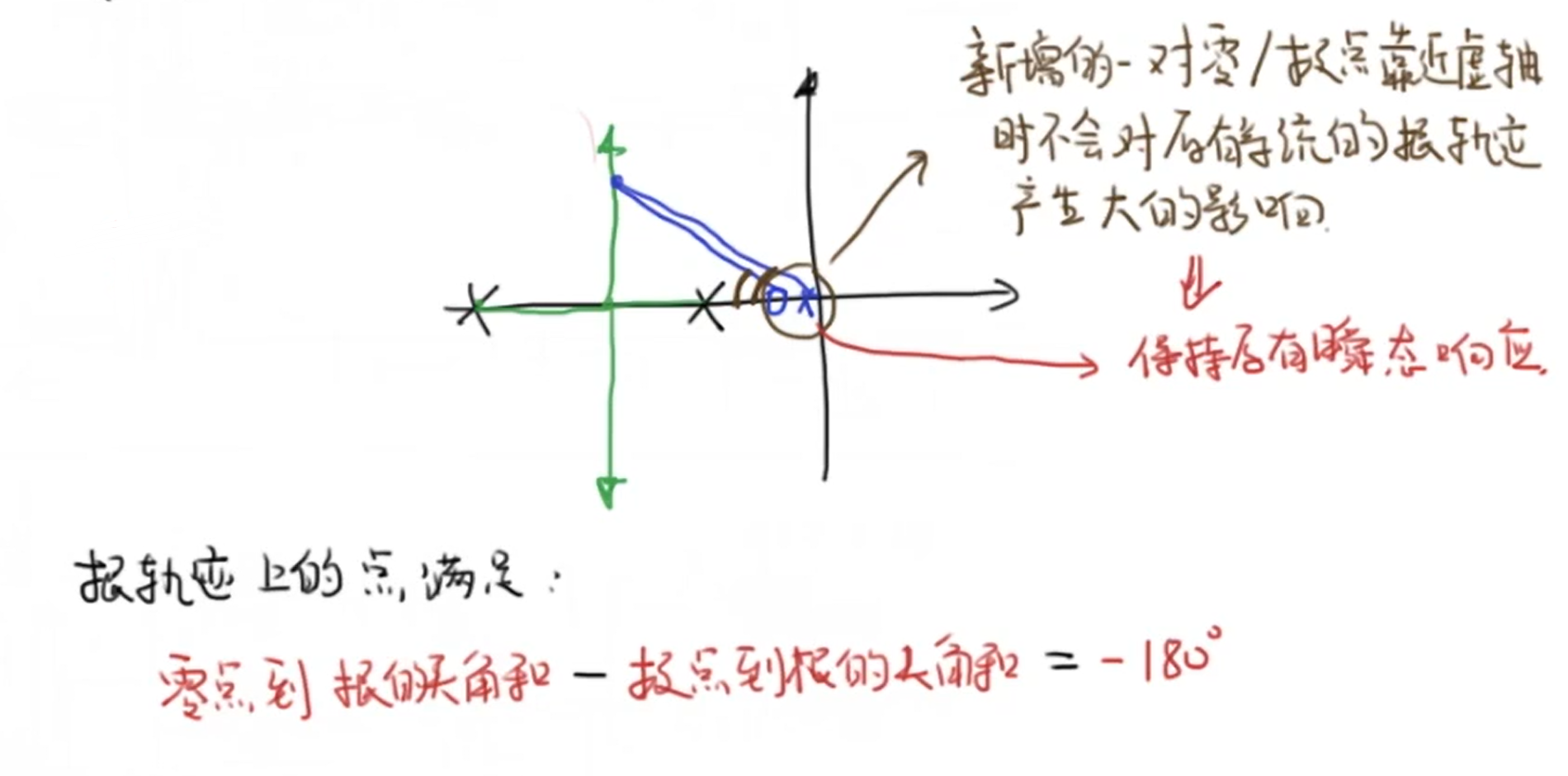
造成红蓝这种差异的原因,我们可以通过根轨迹的角度来分析。首先我们添加补偿器的目的是为了配置极点或者说配置根轨迹,如果极点和零点距离虚轴很近,那他们在保证目标比例的情况下位置就越接近,就像0.1 0.9与1 9这样。而他们两者越接近,他们的差值就越小,对根轨迹渐近线位置的影响就越小。而根轨迹渐近线是系统瞬态响应或是说收敛速度的体现。因此新增的一对零极点越靠近虚轴他们对系统瞬态响应的影响就越小: