在机器学习中,经常要用scikit-learn里面的线性回归模型来对数据进行拟合,进而找到数据的规律,从而达到预测的目的。用图像展示数据及其拟合线可以非常直观地看出拟合线与数据的匹配程度,同时也可用于后续的解释和阐述工作。
这里利用Nathan Yau所著的《鲜活的数据:数据可视化指南》一书中的数据,学习画图。
数据地址:http://datasets.flowingdata.com/unemployment-rate-1948-2010.csv
准备工作:先导入matplotlib和pandas,用pandas读取csv文件,然后创建一个图像和一个坐标轴
import pandas as pd from matplotlib import pyplot as plt unemployment=pd.read_csv(r"http://datasets.flowingdata.com/unemployment-rate-1948-2010.csv") fig,ax=plt.subplots()
让我们先来看看这个数据文件(此处只截取部分):
Series id Year Period Value 0 LNS14000000 1948 M01 3.4 1 LNS14000000 1948 M02 3.8 2 LNS14000000 1948 M03 4.0 3 LNS14000000 1948 M04 3.9 4 LNS14000000 1948 M05 3.5 .. ... ... ... ... 716 LNS14000000 2007 M09 4.7 717 LNS14000000 2007 M10 4.7 718 LNS14000000 2007 M11 4.7 719 LNS14000000 2007 M12 5.0
这个数据展示的是美国1948年到2010年各月份的失业率。
我们需要先把数据用散点图画出来,再用sklearn对数据进行拟合,最后把拟合线也画出来。
首先,把年份和失业率数据提取出来,画出散点图。这里需要注意的是,年份数据比失业率数据规模大很多(年份以千计,失业率大部分是个位数),因此在拟合前需要进行特征缩放,否则年份这一特征值的影响将远远大于失业率。
其次,从sklearn导入线性回归模块。假设数据模型属于简单线性回归,此时,就是把年份数据当作自变量(通常记为变量x),失业率数据当作因变量(通常记为变量y),找出它们之间的线性关系。然后在散点图上画出此拟合线。需要注意的是:年份数据是一维数组,需要将其转换为二维矩阵(这个矩阵的每一列为各个特征的量化值,每一行为每个样本的观测数据),才可以用sklearn进行拟合。通常通过x.reshape(-1,1)方法或x[:,np.newaxis]方法将其转换。
此时图像如下:
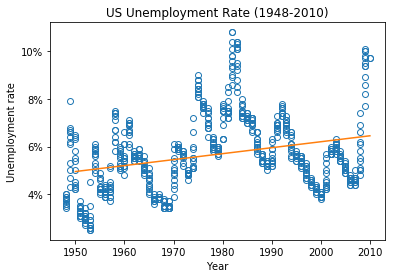
可以看出,这条拟合线并不能很好反映出数据的pattern。
所以接下来,我们再用多项式回归模型来试一试。sklearn里面并没有直接的多项式回归模块可供我们使用,而是需要从sklearn.preprocessing导入PolynomialFeatures,在PolynomialFeatures里确定进行几次多项式变换,将年份自变量转换为多项式形式,然后再用线性模型进行拟合。例如:假设年份自变量为:
[[19] [20] [21]]
那么将其转换为二次多项式形式(degree=2)后就变成:
[[1 19 361] [1 20 400] [1 21 441]]
这样就相当于把原有的方程式y=b1x+a转换成了y=b1x+b2x2+1+a。
完整代码如下:
import numpy as np import pandas as pd import matplotlib from matplotlib import pyplot as plt unemployment=pd.read_csv(r"http://datasets.flowingdata.com/unemployment-rate-1948-2010.csv") fig,ax=plt.subplots(figsize=(10,6)) #提取年份和对应的失业率数据,由于年份数据都是上千,而失业率大都是个位数, #因此这里要用到特征缩放,把年份缩小100倍 x=unemployment["Year"].values/100 y=unemployment["Value"].values #以年份为x轴,失业率为y轴,画出散点图 ax.plot(x,y,"o",markerfacecolor="none") ax.set(xlabel="Year",ylabel="Unemployment rate",title="US Unemployment Rate (1948-2010)") ax.yaxis.set_major_formatter(matplotlib.ticker.FormatStrFormatter('%.f%%')) #把y轴刻度值设置为百分比形式 ax.set_xticklabels(np.arange(1940,2011,10)) #设置x轴刻度标签 #假设数据属于简单线性回归,对其进行拟合 from sklearn.linear_model import LinearRegression linear=LinearRegression() xfit=x.reshape(-1,1) yfit=y.reshape(-1,1) linear.fit(xfit,yfit) xpre=np.linspace(19.5,20.1,num=50,endpoint=True) #创建用于预测的x值 ypre=linear.predict(xpre[:,np.newaxis]) ax.plot(xpre,ypre,"-",label="degree 1") #假设数据属于多项式回归,分别对其进行拟合 from sklearn.preprocessing import PolynomialFeatures for i in [2,4]: PF=PolynomialFeatures(degree=i) xfit1=PF.fit_transform(xfit) linear1=LinearRegression() linear1.fit(xfit1,yfit) xpre1=PF.fit_transform(xpre[:,np.newaxis]) ypre1=linear1.predict(xpre1) ax.plot(xpre,ypre1,"-",label="degree {}".format(i)) ax.legend() plt.show()
图像如下:
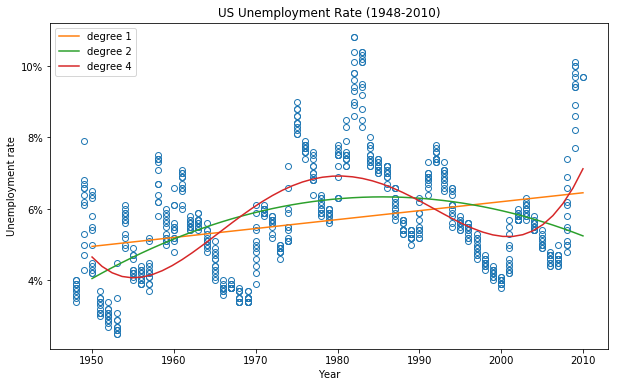
可以看出,用多项式回归模型进行拟合的效果比较好。