LeetCode40. 组合总和 II

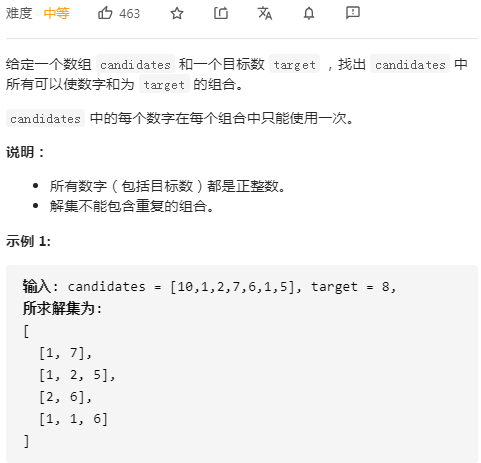
思路：回溯搜索 + 剪枝。

　　注意，回溯做选择的方法，不适用于有 “有重复元素的数组”。因此，重点掌握 常规回溯算法的写法。

class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(candidates); // 排序
        dfs(candidates, 0, target, new ArrayList<>(), res);
        return res;
    }
    private void dfs(int[] nums, int start, int target, List<Integer> list, List<List<Integer>> res) {
        if (target == 0) {
            res.add(new ArrayList<>(list));
            return;
        }
        for (int i = start; i < nums.length; i++) {
            if (target < nums[i]) break; // 大剪枝，后面全是大于target的，直接跳出
            // 对同一层数值相同的节点的第2、3..个节点剪枝，因为数值相同的第一个节点，已经搜出了包含这个数值的全部结果
            if (i > start && nums[i] == nums[i-1]) continue; // 小剪枝，避免了同一层的重复
            list.add(nums[i]);
            dfs(nums, i + 1, target - nums[i], list, res);
            list.remove(list.size() - 1);
        }
    }
    // 回溯做选择 (XX)
    // 行不通,无法去重: [ [1,1,6],[1,2,5],[1,7],[1,2,5],[1,7],[2,6] ]
    private void dfs1(int[] nums, int index, int target, List<Integer> list, List<List<Integer>> res) {
        if (index == nums.length) return;
        if (target == 0) {
            res.add(new ArrayList<>(list));
            return;
        }
        if (target < nums[index]) return;

        list.add(nums[index]);
        dfs1(nums, index + 1, target - nums[index], list, res);
        list.remove(list.size() - 1);

        dfs1(nums, index + 1, target, list, res);
    }
}